

Cover | TOC


Problems | Answers
Farmers must be a lot smarter than we tend to give them credit for being. These
math and logic puzzles that appeared in the 1961 Old Farmer's Almanac are not a
duffer's
task to complete. Be careful to consider units of measure based on the venues
(farming, shipping, etc.).
Puzzle I is a relatively simple trigonometry problem, although the wording of
the problem statement is very confusing; it took some head scratching to figure
out what was meant. My answer is off from theirs - probably due to working it out
with an electronic calculator rather than an slide rule (i.e., rounding errors).
Puzzle II is somewhat shocking in its constitution, but considering the era,
not so surprising.
 [Index] [Index]
Reproduced here are various Mathematical Puzzles from
The Old Farmer's Almanac,
published continuously since 1792. All copyrights hereby acknowledged.
|
Puzzle III
required me to opt for a graphical solution since I could not come up with enough
independent equations for the number of unknowns. If you look at the OFA page scan,
you will see typesetter's errors that add to the difficulty. The provided solution
is no help either, at least for me.
Puzzle IV seems utterly nonsensical, but it is actually legitimate); in fact,
I was convinced it was also a typesetter's error until I looked at the answer and
figured out what was expected. Maybe those types of challenges were common in 1961
and didn't need to be explained to farmers.
Problem V was solved graphically rather than doing the hard geometry. After setting
Visio's page scale to display the proper line dimensions, I created three lines
of the specified lengths with 120° between them at the vertex, then drew an equilateral
triangle that intersected them all at the sides. Visio provided the triangle side
length measurements, so I needed only to calculate the area of the resulting triangle.
My answer, however, is half of the given answer, but I suspect the OFA answer is
wrong. It appears they multiplied the full length of the equilateral triangle base
by the height rather than half the base times the height. I'll be glad to be proven
wrong.
Number VI was easy enough after being certain to use exactly the information
provided in the problem statement (still, it was somewhat ambiguous).
Puzzle VII is left as an exercise for the reader ;-)
Puzzle VIII was a
lead pipe
cinch.
My solution to some of the problems are presented below along with the OFA's
answers. The others are left as an exercise for the reader :-)
Math & Logic Puzzles from the 1961 Old Farmer's Almanac
I
If a pole standing perpendicular, 40 feet in length, when the sun is bearing
south, cast a shadow 88 feet (on level ground) what is the breadth of a river running
due N. E. and S. W. within 22 feet, nearest place on the north side of another pole
230 feet high which at the same time casts the extremity of its shadow 12 feet beyond
the river.

II
There is a story that a ship's crew of 30, half whites and half blacks, were
short of provisions, and it became necessary that half of them should be thrown
overboard. It was agreed that they should be placed in a ring on deck, by the captain,
and that as he counted round and round, every tenth man should be thrown over, until
the crew should be reduced one half. He so placed them that all the blacks were
taken. What was the order of arrangement ? Can you so place them?
III
Two farmers, A and B, purchased a tract of land containing three hundred acres,
for which they paid $600. They wish to divide the tract into farms, so that A will
pay 25 cents per acre more than B, and each one to pay an equal portion of the purchase
money ($300 apiece). How many acres will each man have, and what will it cost him
per acre?
IV
Wood
Mr. being at the . of King of terrors, they perfume for his Quakers and who,
which and what, and they penny for Dr. Hound tis IMAGE HERE Dr. Hay-preservers
and little devil behold scarlet his assistance, but before he arrived the not legally
good
taker
changed color and the was ten
mills for.
V
William owned a tract of land whose three sides were all equal in length, and
the centre of the house was in that particular spot, that the nearest distance to
the three sides was 150, 200 and 230 perches respectively. Required the area of
the equilateral triangle tract in acres and perches?
VI
On a mountain's high summit a person does stand. Whose height is five feet
and four-ninths of a span. As he gazes far out upon the broad deep, A light
from the ocean his vision does meet; But this light was reflected from a beacon
near by, Which stood above water two hundred feet high. If admitting the
distance from the seat of his vision To be just one mile to the point of reflection,
Then the space from this point to the base of the tower, Is quite one hundred
and fifty feet more. Now the thing wished to be known is the perpendicular height
From the base of the mountain to the point at his feet.
VII
There is a house 66 feet long by 72 wide, and from the bottom or foundation of
the building to the peak is 43 feet. Required the distance from either lower corner
of the house to the centre of the peak or ridge-pole?
VIII
If one pin was dropped into the hold of the "Great Eastern" the first week, two
pins the second, four the third, and so on, doubled each week for a year, (52 weeks)
how many pins would there be, what would be the weight of them, allowing 200 pins
to the ounce, and how many "Great Easterns" would be required to carry them, her
tonnage being 22,500 tons?
Answers to Math & Logic Puzzles (as provided in the OFA)
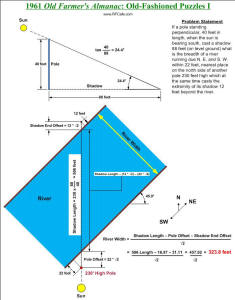
In this case, a picture is needed to explain the Puzzle
I solution to this problem because writing it out would take
1,000
words (or more).
I. Breadth of River, 327.464 feet.
Note: There was a comma in the decimal point place on the printed page - which
is OK for EU and Canadian folks, but confusing to Americans - so I changed it here).
My solution: See graphic to the right.
II. There is a sort of rhyme that used to be our rule
for this, which runs thus:
Two before One,
Three before Five,
Here two, there two;
Save Four alive;
Here one, there one;
Three that are cast,
Now one, twice two;
Whip Jack at last.
My solution: I didn't work this one.
The given method for a solution to problem #3 is a bit fuzzy, so I plotted a
graphical solution based on writing the equation shown from the information provided
in the problem statement.
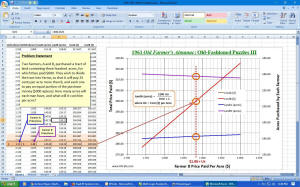
1961 Old Farmer's Almanac Puzzle III Graphical
Solution
III. $2.13,† A's farm per acre. $1.88††
B's farm per acre.
Rule. - Square the average price of one acre. Square the difference
of price between two acres. Add the two squares together. Extract the square root
of the sum. Add the average price of one acre to the result, and you will have the
real price of two acres.
Please to demonstrate the rule.
Solution.
- √(2.0577821² + 0.12½²) + $2.00 = $4.0155643†,
which is the real price of two acres (one of A's
and one of B's).
half sum ± 1/2 difference
Then $2.0577821 + 12½ cents = $2.13278221 †
A's farm per acre;
and $2.0577821 - 12½ cents = $1.88278221
†† B's farm per acre.
My solution: See graphic to the right.
IV. Mr. Underwood being at the point (.) of death (King
of terrors) they sent (perfume) for his friends (Quakers) and relatives (who, which
and what) and they sent (penny) for Dr. Curtis (Hound-tis) who (inclosed) a few
lines (= =) to Dr. Barnes (hay preservers) and imp-lo-red (little devil, behold,
scarlet) his assistance, but before he arrived the invalid (not legally good) died
(changed color) and the (under)taker was cent (ten mills) for.
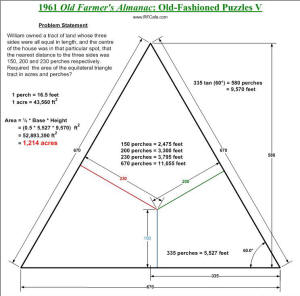
1961 Old Farmer's Almanac Puzzle V Solution
V. 2,427 acres, 121 1/2 rods. (probably wrong)
My solution: See graphic to the right and below.
Note: My answer is half of the given answer, but I suspect the OFA answer is
wrong. It appears they multiplied the full length of the equilateral triangle base
by the height rather than half the base times the height.
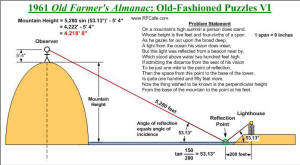
1961 Old Farmer's Almanac Puzzle VI Solution
VI. 4,218 ft., 8 inches.
My solution: See graphic to the right.
VII. 66.4 ft.
My solution: I didn't work this one.

1961 Old Farmer's Almanac Puzzle VIII Solution
VIII. To Curious Question - Number of pins, 4,503,599,627,370,495;
weight, 628,292,358 tons; number of "Great Easterns" required to carry them, 27,924;
she carries one ton of pins to every ton measurement.
My solution: See graphic to the right and below.
Using Algebra Calculator:
# of Pins = 2^52 = 4,503,599,627,370,495
Weight of Pins = 4.503599627370495E15 pins x (1 ounce / 200 pins)
= 22517998136852 ounces
= 1407374883553 pounds
= 31275 long tons
(used in shipping)
# Great Easterns (a ship) = Weight of Pins / 22,500 = 27,924 Ships
Posted June 12, 2018
<Previous
Next>
|


























 "
"










