|
< Previous
Next >
Points of Inflection
 When
reading technical articles, I very often see the authors incorrectly refer to
a certain point on a curve as being the
inflection point. It
is not merely a point at which a curve changes direction. That was the case in an
article I read today that dealt with open-loop polar modulation in EDGE amplifiers.
There exists an unambiguous definition of an inflection point, and all engineers
were taught it in school. Pardon me if this seems trivial or picayune, but the purpose
of the magazine articles is to teach, so if this factoid can eliminate the misconception
in future articles, then it will have accomplished its objective. Here is a brief
review of what an inflection point is, and, equally important, what an inflection
point is not.
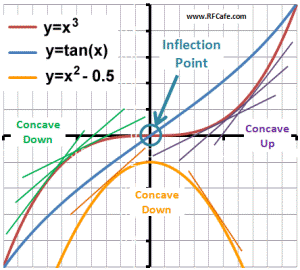
An inflection point is the point at which the second derivative of a continuous
curve equals zero. Accordingly, it is the point where a curve changes from concave
up to concave down. A curved region is concave up if all the data points in that
region lie above a line tangent to it (in the positive-going y-axis direction).
A curved region is concave down if all the data points in that region lie below
a line tangent to it (in the negative-going y-axis direction). The Excel plot that
accompanies this article illustrates all of these concepts. Note that not all curves
have an inflection point, while some curves have many. The two curves shown here
(red and blue) have one apiece.
A familiar inflection point, and quite likely the first one introduced to each
of us in calculus class, is the one that occurs at the 0-axis crossing in a cubic
curve: y = x3. That is the red curve on the graph. Note that all the
points on the left half of the curve lie below the tangent line shown (or any line
tangent to the curve in the left half, and therefore the left half of the curve
is concave down. To the contrary, all the points on the right half of the curve
lie above the tangent line shown (or any line tangent to the curve in the right
half), and therefore the right half of the curve is concave up. The inflection point
on the y=x3 curve is at x=0, y=0. To find that point mathematically,
set the second derivative, d2/dx2 (x3) = 6x, to
zero and get x=0. Finally, y=03=0.
The same situation is true for the half cycle of the tangent curve (blue). The
second derivative of tan(x) is d2/dx2 tan(x) = 2*sec2(x)tan(x),
which is also equal to zero at x=0.
Now, here is where some authors err. Many of the curves we plot look like the
orange plot on the graph. AM/PM conversion, power versus frequency in a bandpass
filter, and component Q-factor plots are a few examples. This plot happens to be
a parabola where y=x2-0.5 (to minimize clutter around the 0-0 crossing).
By inspection, it can be seen that the entire curve lies below any tangent line
drawn. It does not matter whether the tangent line has a positive slope (on the
left half) or a negative slope (on the right half), all points on the curve are
below it. Consequently, this curve, and those like it, have no inflection point.
That this is so can also be shown mathematically since the function y=x2
has no second derivative that can equal zero - it always equals 2*x0
= 2. Therefore there can exist no inflection point.
So there you have it. Let us resolve to never again refer to a local maximum
or minimum (where the first derivative equals zero) on a curve as an inflection
point unless it occurs at a transition between concave up and concave down.
Posted January 17, 2022
(updated from original post on 3/4/2012)
|
"
