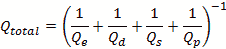Searching for the Q |
|
Sunshine Design Engineering Services Joe Cahak, RF engineer and owner of Sunshine Design Engineering Services, just sent me another paper he has authored on the subject of determining the quality factor ("Q") of rectangular and cylindrical cavities. Before you decide to skip reading this article because the topic might seem too esoteric, Joe does much more than present formulas and tables. He also includes a tale of the research needed to cull and vet the many, often conflicting, opinions of which formulas are correct. Ultimately, a decision was made to select formulas that most closely matched empirically determined (measured) values from published data. If Mr. John T. Frye was still writing Carl & Jerry adventures for Popular Electronics,, this might make a good story line. See list of all of Joe's articles at bottom of page. Searching for the Q By Joseph L. Cahak Copyright 2014 Sunshine Design Engineering Services What is Q? Q, or Quality factor, is the measure of the ability of a cavity or other resonant structure to have and hold energy. Another description is the center frequency of a resonant circuit divided by the 3 dB Bandwidth.
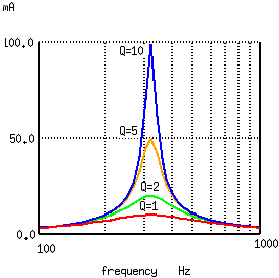
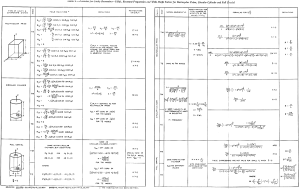
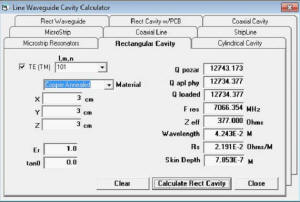
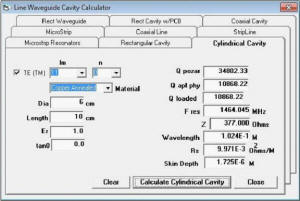
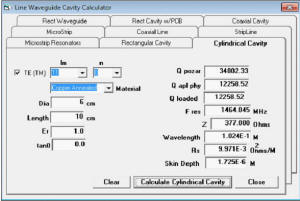
Figure 1 - Bandwidth vs Q of resonant circuit courtesy AllAboutCircuits.com The search for the Q began after I got an email from an engineer at a filter manufacturer. He had purchased my RF Calculator and desired to see if I could add the calculation for rectangular and cylindrical cavities with their Q. His company had something they used internally and he sent me their code to look at. No documentation or details about how to use it was included. So, it wasn't much use, other than to review and see if it matched anything I found; it did somewhat. His calculation was one of the five for the rectangular prism case where the mode orders l, m & n are all non zero. With this article I would like to tell you a story of one of my recent development projects for an addition to my RF Calculator product. I hope you will forgive my indulgence in telling it. I am a consulting RF/Microwave Test Engineer with process automation and application development as specialties. I design, build and program automated test systems. I also do some application development for myself and for sale. I have been in the RF/Microwave business for 30 years collecting reference literature all along. I have a rather large collection of engineering books, notes, articles and digital content. The formulas cover the gamut from RF, microwave, astronomy, physics, math, chemistry, electronics, programming and lots more. Having the formulas at hand and easy to use and understand is key to making them useful. Lugging all the books around is not an option, nor is trying to correctly recalling them all by memory. Over the years I worked in BASIC, Pascal, Fortran, HP Basic, HT Basic, QBasic then Visual Basic 3 thru 6, Borland C and Microsoft C, VB.net, C# and now LabVIEW. The question with software libraries for sale is what language makes it marketable? There are so many different programming environments out there today that targeting a specific language or programming environment is a difficult decision. The programming environments of choice have gone thru many changes over the years. My choice for these calculator applications was a light weight Windows program in Visual Basic. It is easy to program and install and the Windows executable still works on Windows 7 and 8. For more modern RF Test development I program more with LabVIEW now and compile libraries (DLL) and as LabVIEW Libraries. I am considering going to the mobile platform for the applications, but haven't been able to afford the development tools yet. About 15 years ago I started collating the best formulas in my RF Calculator program. I also developed a rather useful astronomy calculation product called AstroCalculator and an astrophotography and optics calculator called OptiCalculator. The calculators were initially developed for my use. I am always on the hunt to find new formulas and features to add to my calculators. RFCalculator had a cavity resonance section, but it was incomplete. It had a rectangular cavity with partial dielectric fill (PCB) and cylindrical cases that needed work and did not perform the Q calculations. The more general solutions for the cylindrical and rectangular prism cases was always preferred, but I saw a lot of work and time to resolve and understand all the information and glean a solution. Life's conditions had to be ripe for the effort. I had some employment uncertainties for a couple of months, so I used the time off to do some special projects while looking for more employment. It was good challenging mental work and kept me occupied and purposed. I had to complete the complex and S-parameter library and functions first. I was able to complete all that sizable effort and finish a salable LabVIEW and C language DLL library to sell for the libraries. I could now tackle the Q. Research for the effort began with a reference search to see what material I could come up with. In the old days searching meant at the book stores, libraries with index cards, books, magazines and microfilm. All of them were very time consuming and book purchases were very expensive. Today, a literature search with the Internet takes only seconds. This is a tremendous resource for the paper-challenged (remote locations w/o books). Going to the library or bookstore used to be easy and cheap, but now with living in the backcountry, distance costs a lot. So, I now order new or used books from Amazon for pennies to dimes on a dollar for some very good used reference books. With Amazon, I found if I added the expensive ones to my wish list, I would see the occasional used deals that allowed me to purchase the odd book for my library for less. I had to be quick for these short flash gems of bound paper. They usually go fast. Just yesterday I was able to finally purchase the Microwave Filters, Impedance-Matching Networks, and Coupling Structures book by Matthaei, Jones and Young for $49.99 instead of the usual $119. My Internet searches not only scan for book or article titles, but also content in them. eBay, Google, Amazon and a slew of companies now deal in used books and a lot of classic technical books that are coming available for very cheap prices as libraries dump their old books. I use this extensively now to grow my engineering and science reference library. The public loss is my gain. I purchased what reference books I could afford. Many of my engineering friend's libraries were scoured and book loans were secured. The search was on to find the general solution for Q of rectangular prisms and cylinders and almost no avenue was left unturned. Initial searches thru the microwave reference books were fair, but showed many poor and incomplete examples for Q formulas that did not cover all the cases for TE and TM modes, so the search continued. For the rectangular prism resonant cavity the coordinates for x, y and z is a-length, b-width and d-height. Other authors use different dimensional symbols and this can confuse novices (like me) on the topic due to many using mode orders (l, m, n) or (m, n, L) and then l for height (Pozar). It quickly gets very confusing. In addition to the dimensions of the cavity a few other things must be determined to perform all the calculations leading up to the Q formulas. We need the type of metal or other surface (like the earth for instance in the spherical case). I also use the metric system of measurements. Matthaei, Jones and Young's book or MJY, as I will refer to it, uses English inch units and also fixes a constant instead of showing the full formulation. Pozar's book has one formula each for the rectangular and cylindrical case. They did not compute well at many instances outside his singular examples. Other books showed a blithering array of variations of the coordinate systems and formulas. Most authors' examples were singular and poorly expounded in most cases, almost as if offhanded, disappointing to be sure. I kept gathering my reference materials and looking it over occasionally when I was bored, usually when the weather was bad or it got dark early in winter. I kept trying Google searches to see what I could find and discovered that search phrases could bring big differences in the search results. I was also finding a lot of protected content on the MTT, Journal of Applied Physics and many other more obscure sites and other references too numerous to mention. They only showed partial content if any. One day while Web searching, I finally stumbled on the first of the Bell System Technical Journal or BSTJ notes in the references. I had been using Cavity Resonance Q and Microwave Cavity Q in my searches to no avail. I then tried a different variation on search string and used Microwave Cavity Testing and there was a paper from “BSTJ” and had volume numbers on them. The two papers had the same Applied Physics Journal table of formulas, see figure 1. I found out later that these papers were from Bell System Technical Journal and that they had the tables, formulas and charts that helped a lot. I now had at least three independent references for the full general Q methods to use for the various mode cases. Several of the links to this and other referenced papers are only available to subscribers. I happen to find a site or so that had the PDF copies available. I also found several related references from the same Bell Systems Technical Journal which I was also able to find copies of. These references had the same copy of the table of cavities and there reference formulas. Rectangular had 5 total cases, the cylindrical had three cases and the coaxial has three cases. I was seeing cross agreement with MJY for the rectangular and Collin's formulas for cylindrical. I also found a reference to the full tables in the Microwave Engineer's Handbook Volume 1. The coaxial case was where the only difference occurred. Also the BSTJ had the full formulation and in metric units, so the formulas had no constants other than expected physical constants. Figure 2 - Cavity Formulas The next step was to work up the formulas and test them. I used Mathematica for the formulation and testing. It was easy to enter the formulas and test them. I made some changes to the variables to help me cross over to several authors' formulas simultaneously. They needed to be tested over the range of typical values. I was successful at this stage and was starting to notice trends in the values calculated and whether they were consistent over TM/TE modes and modal states. All the most significant resonant cases were run for testing the Q formulas against each other, and results were gathered. I still had the problem of determining how could I better test my values to know if the ranges I was seeing were reasonable? I had just a few examples from the books and articles to go by, but wanted better data. The MJY reference gives the Q as a compound function. The charts are difficult to interpret. Re-reading thru all the references again I found some statements in Collin's book “Foundations of Microwave Engineering”. He gave the expected range for cylindrical cavity as 10000 to 40000 with wavelengths in the 3cm range as having optimal Q. He also gave a 3x3x3cm cube in copper Q as 12700. My calculations produced 12734.3 (see Figure 2). I was beginning to have some level of confidence in the calculations. Figure 3 - 3x3x3 cm Rectangular Cavity After all the formulas had been tested in Mathematica, I next performed the coding and testing in my RF Calculator program. I had to work out an interface for the mode options and present them in a easy to understand and use format. This also required looking further into the TE and TM modes and the most commonly used modal orders so I could bring some containment to the interface, yet provide a wide selection. I also had to allow the user to select between the surface material and the tangent loss and dielectric constant. Figure 4 – Rectangular Cavity screen Figure 5 – Cylindrical Cavity screen As can be seen in the screenshots answers are provided to a number of cavity values like the wavelength,
sheet resistivity, characteristic impedance and the skin depth along with the loaded and unloaded cavity
Q, resonant frequency and both the Applied Physics value for Q from BSTJ and the Pozar value for Q.
Loaded Q uses the formula
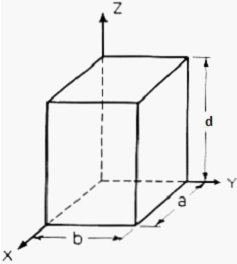
Rectangular Prism Cavity
Figure 6 - Rectangular Prism Cavity The formulas for the power are complex integrals of three dimensions. For the electric field the formula is
Or for the magnetic fields
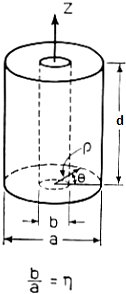
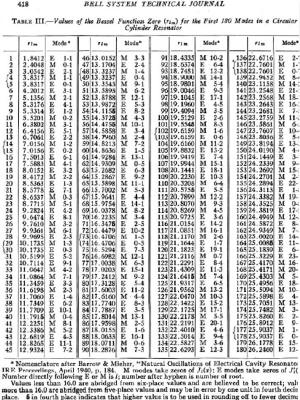
For the rate of loss or just “loss” we use the skin depth calculated below Resistivity of copper is ρ=5813000 mhos/meter or S/m. μo =4π10-7 H/meter Characteristic impedance Z or Sheet resistivity or Skin depth or We calculate by defining the coordinates, dimensions, modes and mode orders x=a; y=b and z=d. The corresponding mode orders are l, m and n for the x, y and z axis and a, b and d length. We are calculating for a half cycle or half wavelength. The definitions used for the calculation Wavelength or Resonant Frequency For TE mode order l, m > 0 For TE mode order l = 0
For TE mode order m = 0
For TM mode order n > 0
For TM mode order n = 0
Rectangular Modes Table The table shows the various rectangular cavity modes and mode orders as functions of the dimensions and frequency. Figure 7 - Rectangular Cavity Models Chart Cylindrical Cavity
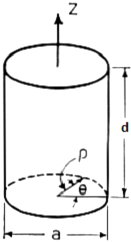
Figure 8 - Cylindrical Cavity The formula for the cylindrical cylinder power is a complex integral of 3 dimensions. For the rate of loss or “loss” we use the skin depth calculated below Resistivity of copper is ρ=5813000 mhos/meter or S/m μo =4π10-7 H/meter Characteristic impedance Z or Sheet resistivity or Skin depth or We again calculate using the coordinate, dimensional mode and mode order definitions. The diameter=a and the height or z=d. The corresponding mode orders are l, m and n for the x, y and z axis and a diameter and d length. The l and m mode orders are not addressed the same for cylindrical cavities. For these, the zero order Bessel J0 for the TM modes and first derivative (prime) Bessel Jp0 are used for the TE modes. These Bessel zero values can be looked up in mathematical tables. See table in figure 8. In this case the J0 and Jp0 values are interspersed and marked by the E or M mode and the mode order from lowest order out to 180th order. For TE mode The definitions used for the calculation Wavelength or Resonant frequency
For TM mode The definitions used for the calculation Wavelength or Resonant frequency
when mode order n>0
when mode order n=0
Cylindrical Modes Table of Bessel Functions Figure 9 - Cylindrical Modes Table of Bessel Functions Corrections for Q Q is a complex thing and is comprised not only of the power storage/loss mechanism Qe , but also
by other effects. Dielectric materials used for cavity fill can cause a power loss resulting in
Coaxial, Spherical and other Cases
Figure 10 – Coaxial Cylinder The coaxial cylinder case can be seen in the BSTJ documents and is quite lengthy. I have not yet tackled that or the spherical and elliptical cases. In the article “Redefining the Kelvin” an elliptical cavity was used to get a very accurate value for the Kelvin and Boltzmann's constant (k). For the spherical cavity case, in Lecture Notes 10.5 they discuss the Earth's spherical resonance with Lightening stimulation. The reader can pursue further studies in these areas if they desire. Maybe the next long bout of extended time off and bad weather I will tackle the coaxial and spherical Q cases. For now I am satisfied having resolved the rectangular and cylindrical cases to add to my calculator functions. I would like to thank you the reader for allowing my indulgence with “Searching for the Q”. References Links
Sunshine Design Engineering Services is located in the sunny San Vicente Valley near San Diego, CA, gateway to the mountains and skies. Are you looking for new things to design, program or create and need assistance? I offer design services with specialties in electronic hardware, CAD and software engineering, and 25 years of experience with Test Engineering services in RF/microwave, transceiver and semiconductor parametric test, test application program development, automation programs, database programming, graphics and analysis, and mathematical algorithms. See also: - Noise and Noise Measurements - Measuring Semiconductor Device Input Parameters with Vector Analysis - Computing with Scattering Parameters - Measurements with Scattering Parameters - Ponderings on Power Measurements - Scattered Thoughts on Scattering Parameters Sunshine Design Engineering Services 23517 Carmena Rd Ramona, CA 92065 760-685-1126 Featuring: Test Automation Services, RF Calculator and S-Parameter Library (DLL & LLB)
Posted March 13, 2014 |
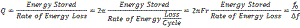
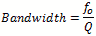
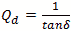 for the Q of the dielectric in the cavity.
Adding this in parallel with the cavity Q produces the total Q.
for the Q of the dielectric in the cavity.
Adding this in parallel with the cavity Q produces the total Q.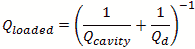
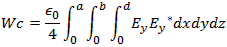
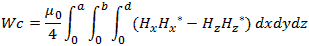
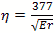 Ohms
Ohms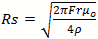 Ohms/Square
Ohms/Square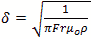 cm
cm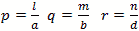
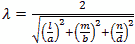 cm
cm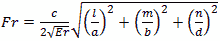 Hz
Hz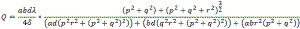
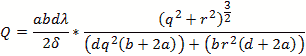
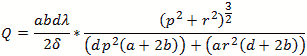
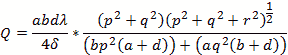
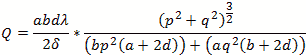
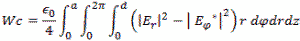
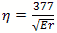 Ohms
Ohms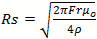 Ohms/Square
Ohms/Square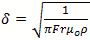 cm
cm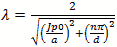 cm
cm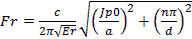 Hz
Hz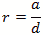
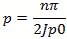
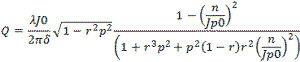
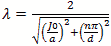
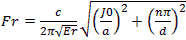
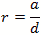
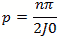
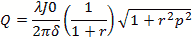
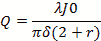
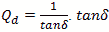 is the dielectric tangent loss. Another
Q factor is the surface roughness Qs and finally Qp is any perturbations to the geometry
such as a small aperture and electric probe wire. These addition Q factors are summed by the parallel
sum method.
is the dielectric tangent loss. Another
Q factor is the surface roughness Qs and finally Qp is any perturbations to the geometry
such as a small aperture and electric probe wire. These addition Q factors are summed by the parallel
sum method.