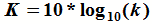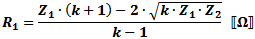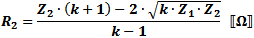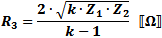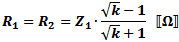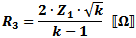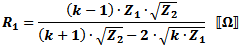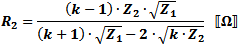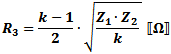|
Fixed attenuators can be designed to have either equal or unequal impedances and to
provide any amount of attenuation (theoretically) equal to or greater than the configuration's
minimum attenuation - depending on the ratio of Z1/Z2. Attenuators
with equal terminations have a minimum attenuation of 0 dB. Unequal terminations
place a lower limit on the attenuation as follows:
 , for Z1
> Z2 in circuits shown below
Express in
decibels as: 
In the attenuator formulas below:
 , which is the linear attenuation
ratio of the two powers or voltages (note that "k" has a minimum value
if Z1 and Z2.are not equal).
If, as is typical, the attenuation is given in decibels (K
dB vs. k), then convert to a ratio as follows:
 <———>
An online attenuator calculator is provided
at the bottom of the page.
|
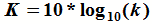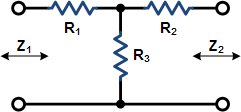
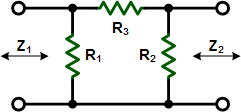
These equations apply to the two
forms of Tee attenuators at the left.
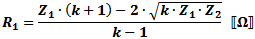
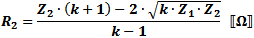
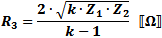
If Z1 = Z2, then:
|
 |
 |
|
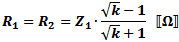
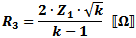
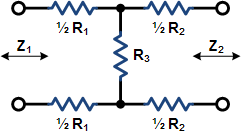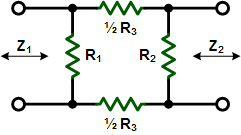
These equations apply to the two
forms of Pi attenuators at the left.
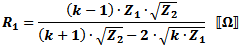
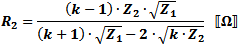
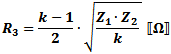
If Z1 = Z2, then:
|
 |
 |
|
Note:
Only enter values in the yellow cells or risk overwriting formulas! |
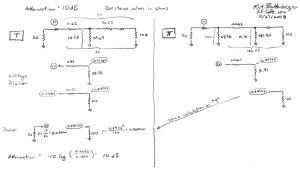
An RF Cafe visitor wrote to say that he thought the above equations might be in error
when unequal source and load termination resistances are used. The image below shows
the mathematical steps that prove the equations are correct. It uses a source resistance
of 50 ohms and a load resistance of 100 ohms, with an attenuation of 10 dB. Resistor
values for both the "T" and ""Pi" attenuators were determined using the
attenuator calculator
on RF Cafe (which uses these equations).
|
