Boolean Algebra Equations & Truth Tables

British mathematician George Boole developed a form of algebra that uses symbolic logic to define relationships in sets - unions and intersections to be precise. In electrical engineering, we do not usually bother ourselves with all the rigors and formalities of the pure mathematical application. Rather, since engineers actually build things that perform useful functions, most of us can get by with the basic operations presented below.

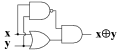
Venn Diagrams do not help much when designing a digital circuit where complex (or simple for that matter) conditional decisions must be made to determine the proper output of a multiplexer or an entire production line controller circuit. Instead, we use Truth Tables, State Machines and Karnaugh Maps.

There are three fundamental operators from which all other Boolean functions can be derived - the OR gate, the AND gate, and the NOT (negation) operator. The Exclusive OR gate is included even though it is not a fundamental function, but it is very commonly used. Venn Diagrams for each of the functions are give just for illustration. White regions are where the functions are True, and blue areas are False.

OR x y x + y 0 0 0 0 1 1 1 0 1 1 1 1 The OR Symbol •

AND x y x · y 0 0 0 0 1 0 1 0 0 1 1 1 The AND Symbols +

Exclusive OR x y x y 0 0 0 0 1 1 1 0 1 1 1 0

NOT x x 0 1 1 0 The NOT Symbol °

Identities
	x + 0 = x	x · 1 = x
	x + x = 1	x · x = 0
	x + x = x	x · x = x
	x + 1 = 1	x · 0 = 0
Theorems
Involution
Commutative	x + y = y + x	x · y = y · x
Associative	x + (y + z) = (x + y) + z
Distributive	x · (y + z) = x · y + x · z	x + y · z = (x + y) · (x + z)
DeMorgan	(x + y) = x · y	(x · y) = x + y
Absorption	x + x · y = x	x · (x + y) = x