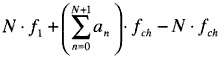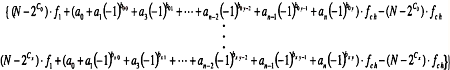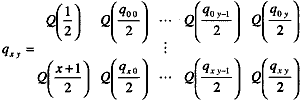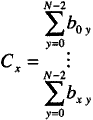|
by Chris Arnott
A web exclusive from CED Magazine
Note: This paper used to be available on the
CED (Communications Engineering &
Design) website, but has been removed. So, I scanned the copy provided to me by
the author, Chris Arnott, when we worked together at RFMD. I will remove the article
at the request of CED.
| 1 |
2 |
3 |
4 |
121.25 |
6 |
521 |
242.5 |
254.5 |
266.5 |
278.5 |
| 2 |
3 |
4 |
5 |
|
|
545 |
254.5 |
266.5 |
278.5 |
290.5 |
| 3 |
4 |
5 |
6 |
|
|
569 |
266.5 |
278.5 |
290.5 |
302.5 |
| 4 |
5 |
6 |
7 |
|
|
593 |
278.5 |
290.5 |
302.5 |
314.5 |
| 5 |
6 |
7 |
8 |
|
|
617 |
290.5 |
302.5 |
314.5 |
326.5 |
| 6 |
7 |
8 |
9 |
|
|
641 |
302.5 |
314.5 |
326.5 |
338.5 |
| 7 |
8 |
9 |
10 |
|
|
665 |
314.5 |
326.5 |
338.5 |
350.5 |
| 8 |
9 |
10 |
11 |
|
|
689 |
326.5 |
338.5 |
350.5 |
362.5 |
| 9 |
10 |
11 |
12 |
|
|
713 |
338.5 |
350.5 |
362.5 |
374.5 |
| 10 |
11 |
12 |
13 |
|
|
737 |
350.5 |
362.5 |
374.5 |
386.5 |
Chris Arnott, RF Micro Devices (formerly)
Cable operators offering digital communication services on their systems provide
customers with Internet access, digital video and business network solutions to
add flexibility and profitability to their systems. A major system consideration
for successful implementation of a modem digital cable system is system linearity.
Inadequate system linearity distorts the channel information and can lead to low
system operability or reliability.
Amplifying components placed within the system for signal amplification or frequency
conversation contribute to system distortion. All amplifiers and frequency conversion
components exhibit non-linear amplification and produce distortion, causing intermodulation
products. This distortion corrupts the channels and can lead to high bit-error rates.
The problem is more severe in these wideband cable systems because each amplifying
component input sees the entire high-power multichannel cable system spectrum.
The number of distorting intermodulation products created by these inline-amplifying
components is very large. Worse, many of these intermodulation products fall within
the same channels and the distortion power accumulates with the number of products.
This accumulated distorting power is the main reason why poor system linearity can
cause low system reliability. Therefore, care must be taken when selecting amplification
components for wideband cable systems in order to ensure adequate system linearity.
This paper shows a general algorithm to calculate the number of distortion products
created by a third-order non-linearity in a wideband multichannel system.
This article describes a general algorithm to calculate the frequency locations
of third-order intermodulation distortion products produced by a broadband amplifier
for any number of test tones. It also defines a broadband system with equally spaced
channels. The analysis includes a calculation of total primary and intermodulation
product signals produced by non-linear third-order systems and a discussion of where
the most important intermodulation distortion products lay. A practical example
of a four-tone test is then performed on a standard IRC cable TV system with third-order
non-linearity.
on-linearity of amplifiers in broadband applications greatly contributes to system
performance degradation because of interfering distortion signals. Broadband systems
containing many equal-power channels produce intermodulation distortion signals
when amplified by line amplifiers and LNAs.
Narrowband systems readily use simple two-tone tests to analyze third-order intermodulation
distortion [1]. Narrowband intermodulation analysis is simplified by ignoring distortion
products not located within close proximity of the desired channel. These simplifications
cannot be readily utilized in broadband system intermodulation distortion analysis
many intermodulation products lie within the system bandwidth. Intermodulation distortion
analysis is more difficult in broadband systems because all intermodulation products
can interfere with many channels simultaneously Therefore, broadband systems require
multi-tone tests to analyze third-order intermodulation distortion.
Third-Order Broadband System Distortion Analysis
Broadband systems are comprised of many equally spaced channels.
A broadband system with equally spaced multi-channels is described by equation
1,
fi = f1 + (i -1) · fch
for i = 1,2,3,···, N + 1 Eq. 1
where i represents the channel number, f1 represents the beginning channel frequency,
represents the number of channels, and fch represents the channel spacing. A non-linear
third-order distorting amplifier produces four types of tones: the primary; the
third harmonic; the third-order intermodulation products; and frequency sum products.
The terminology, "third-order intermodulation product" is traditionally used
to define the important intermodulation products in narrowband analysis. This terminology,
though technically incorrect, is used to define the same products in broadband intermodulation
analysis and will be clarified later. The third harmonic, third-order products,
and frequency sum products are interference signals that degrade desired channel
reception. The amplifier passes all N primary tones and generates a total of N third
harmonic distortion tones. The number of third-order intermodulation distortion
products produced by the amplifier is given by equation 2.
N3rd = 2 · N · (N -1) for N ≥ 2
Eq. 2
The number of frequency sum distortion products generated by the amplifier is
given by equation 3.
Nsum = 2N-1 for N ≥ 2
Eq.3
Combining the number of primary and third harmonic tones and equations 2 and
3, the total number of tones at the amplifier's output is given by equation 4.
NTOT = 2 · N + 2 · N ·(N-1) + 2N-1
for N ≥ 2 Eq.4
The total number of output tones increases dramatically as the number of channels
increases, which indicates the importance of good system linearity because each
distortion tone can potentially distort a channel. The frequency sum products are
the largest number and strongest interfering distortion products and contribute
more to desired signal degradation [23]. The power frequency sum distortion products
are 6 dB higher than the third-order products [3]. The higher power and greater
number is the reason the frequency sum products are considered the most important.
The frequency location of intermodulation distortion interferers in a broadband
system with third-order non-linearity is investigated by applying N arbitrary channel
frequency tones. Each tone is assumed to be of equal amplitude and have zero degree
correlated phase. The N tones in an arbitrarily spaced N-channel system are defined
using equation 1 as
fa0 = f1 + (a0 - 1) · fch
fan = f1 + (an -1) · fch
Eq.5
where an is a positive non-zero successively increasing sequence of integers
given by
Using a composite input signal formed by a summation of cosine functions with
frequencies a broadband system intermodulation analysis can be performed. The non-linear
amplifier is simulated as a third degree monomial with a coefficient of one or gain
of one. Cubing the composite function and using trigonometric identities the frequency
locations of the output tones are found as four distinct sequences as given by,
for the primary tones (see equation 7)
for the third harmonic tones (see equation 8),
and third-order intermodulation products (see equation 9),
| {2 · fan ± fam} |
N |
for m ≠ n |
Eq.9 |
| m=0 |
The definition of the third-order intermodulation given in equation 9 is the
same as for tones used to describe intermodulation distortion in narrowband analysis.
Three sequences describe the frequency sum products. The first and last sum products
are unique where the first product location is given by equation 10,
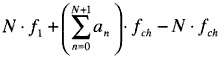 Eq.10 Eq.10
and the last term is located at (see equation 11),
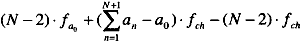 Eq. 11 Eq. 11
The sequence for the frequency locations of the remaining sum products is given
by (see equation 12),
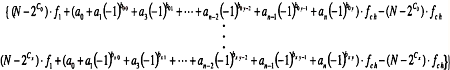 Eq.12
Eq.12
where
x = 0, 1, 2, · · ·, 2N-1 - 1, 2N-1 - 2,
2N-1 - 3, Eq. 13
and
y = 0, 1, 2, · · ·, N - 4, N - 3, N - 2
Eq.14
Exponent bxy is an element in Bxy that describes the base 2 binary digits of
x + 1 for each x state with N -1 significant bits and Cx is the sum of the binary
digits represented by row elements bxy. The sequence described in (12) locates the
sum product frequency locations by negating coefficients a1 - an for all possible
x states. Matrix Bxy ~d vector Cx are found with numerical base 2 conversion techniques.
First a calculation of an x by y matrix containing the quotients of state x divided
by 2 in column 0 is given by equation 15.
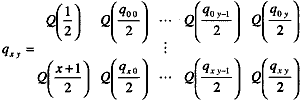 Eq.15 Eq.15
The x by y matrix Bxy contains elements with the remainders of state x+ 1 divided
by 2 in column 0 is given by equation 16,
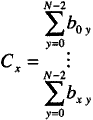 Eq.16
Eq.16
where the row elements represent base 2 binary digits of x+ 1 to N-l significant
bits. The vector Cx is the summation of the row elements of Bxy as given by equation
17
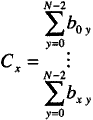 Eq.17
Eq.17
As an example, a system exhibiting third-order non-linearity is subjected to
a four-tone test using equations 5 through 17. The four equally spaced tones are
defined using equation 5 as
fa0 = f1 + (a0 - 1) · fch
Eq. 18
fa1 = f1 + (a1 - 1) · fch
Eq.19
fa2 = f1 + (a2 - 1) · fch
Eq. 20
and
fa3 = f1 + (a3 - 1) · fch
Eq.21
A total of 40 tones are generated by the non-linear system: four primary tones;
four third-harmonic tones; 24 third-order intermodulation products (from equation
2); and eight frequency sum products (from equation 3). The primary tones, third-harmonic
and third-order intermodulation tones using equations 7, 8 and 9 are given by
{fa0, fa1, fa2, fa3}
Eq.22
{3 · fa0, 3 · fa1, 3 · fa2,
3 · fa3}
Eq.23
and
{2 · fa0 ± fa1, 2 · fa0 ±
fa2, 2 · fa0
± fa3,
2 · fa1 ± fa0, 2 · fa1 ±
fa2, 2 · fa1
± fa3,
2 · fa3 ± fa0, 2 · fa3 ±
fa1, 2 · fa3
± fa2, }
Eq.24
The sum product frequency locations for the four-tone test are found using equations
10 through 17. The first and last frequency sum product using equations 10 and 11
are given by
4 · f1 + (a0 + a1 + a2
+ a3) · fch - 4 · fch
Eq.25
and
2 · f1 + (a3 + a2 + a1
- a0) · fch - 2 · fch
Eq.26
The first step in finding the remaining sum product frequency locations is calculating
matrices qxy and Bxy with x and y having six states and three significant bits.
Using equation 15, qxy and Bxy are given by
| qxy = |
0 0 0 |
| 1 0 0 |
| 1 0 0 |
| 2 1 0 |
| 2 1 0 |
| 3 1 0 |
Eq.27
and
| Bxy = |
1 0 0 |
| 0 1 0 |
| 1 1 0 |
| 0 0 1 |
| 1 0 1 |
| 0 1 1 |
Eq.28
Using equation 17, the vector Cx is given by
Cx =1 1 2 1 2 2 Eq.29
Knowing bxy and Cx the remaining sum product frequency location sequence using
equation 12 is given by
{2 · f1 + (a0 - a1 + a2
+ a3) · fch - 2 · fch
2 · f1 + (a0 + a1 -
a2 + a3) · fch - 2 · fch
(a0 - a1 - a2 + a3)
· fch
2 · f1 + (a0 + a1 +
a2 - a3) · fch - 2 · fch
(a0 - a1 + a2 - a3)
· fch
(a0 + a1 - a2 - a3) · fch
} Eq.30
An investigation of the frequency sum distortion products in a real broadband
system is investigated by applying four arbitrary, successively increasing frequency
tones to a system with third-order non-linearity. The tones are assumed to have
equal amplitude and a correlated phase of zero degrees. Phase correlation between
the test tones causes correlation between the intermodulation products. This correlation
between the intermodulation products causes products falling on the same channel
to add as voltages and is considered worst case. Each intermodulation product falls
within close proximity to a channel in systems with no correlation between tones
and appears like a noise signal. This noise like signal is the sum root mean square
power of each distortion product and causes less distortion compared to a correlated
system.
The beginning channel frequency fl is chosen as 121.25 MHz, standard IRC cable
TV video carrier frequency with 6 MHz carrier spacing. The fourth tone is 18 MHz
greater than fl. The bandwidth of the system for investigation of the distortion
products is 624 MHz. Tones a0 - a3 are chosen as four successively increasing frequencies
for cases a0 equal 1 through 10.
A result of (30) for an even number of tones is constant distortion product frequencies
for products with an equal number of positive and negative an coefficients. These
constant product frequencies can be ignored because they do not lie above the beginning
channel. The frequency locations of the non-constant frequency sum distortion products
are shown in table 1. Each distortion sum product in table 1 lies within a channel
in a typical cable TV system, and will interfere with desired channels.
Interestingly, the frequency sum products in the last four columns fall in at
the same frequency as second-order intermodulation (composite second order) products
at +1.25 MHz offset form the carrier. This indicates a system with four much higher
power carriers relative to the remaining carriers can produce third-order products
that appear as second-order products.
Conclusion
Results show that broadband intermodulation distortion analysis cannot utilize
assumptions used in narrowband system analysis. The ignored frequency sum products
in narrowband analysis can distort channels in broadband systems. Results of equation
3 show the number of interfering sum products greatly increase as the number of
channels increase in a broadband system with third-order non-linearity. The algorithm
correctly calculates the distortion product frequency locations for the general
case of any number of test tones.
Acknowledgements
The author thanks Dr. Bruce Schmukler, Greg Schramm, and Jennifer Ameling of
RF Micro Devices for many useful comments and discussions related to this article.
References
[1] T. H. Lee, The Design of CMOS Radio-Frequency Integrated Circuits.
Cambridge, U.K.: Cambridge Univ. Press 1998.
[2] Some Notes on Composite Second and Third Order Intermodulation Distortions,
Matrix Technical Notes MT -108, Matrix Test Incorporated, 12/1998
[3] The Relationship of Intercept Points and Composite Distortions,
Matrix Technical Notes MTN-109, Matrix Test Inc., 2/1998
-- Chris Arnott
Posted May 7, 2024
(updated from original post
on 8/1/2005)
|