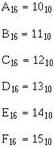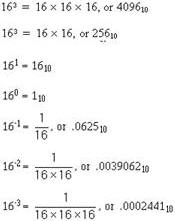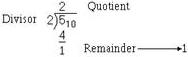Module 13 - Introduction to Number Systems and Logic |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Module 13 − Introduction to Number Systems and Logic Pages i, 1−1, 1−11, 1−21, 1−31, 1−41, 1−51, 1−61, 2−1, 2−11, 2−21, 2−31, 3−1, 3−11, 3−21, 3−31, 3−41, Index
Table 1-5. - Binary and Hexadecimal Comparison
Unit and Number
As in each of the previous number systems, a unit stands for a single object.
A number in the hex system is the symbol used to represent a unit or quantity. The Arabic numerals 0 through 9 are used along with the first six letters of the alphabet. You have probably used letters in math problems to represent unknown quantities, but in the hex system A, B, C, D, E, and F, each have a definite value as shown below:
1-31
Base (Radix)
The base, or radix, of this system is 16, which represents the number of symbols used in the system. a quantity expressed in hex will be annotated by the subscript 16, as shown below:
A3EF16
Positional Notation
Like the binary, octal, and decimal systems, the hex system is a positional notation system. Powers of 16 are used for the positional values of a number. The following bar graph shows the positions:
163 162 161 160 • -1 16-2 16-3
Multiplying the base times itself the number of times indicated by the exponent will show the equivalent decimal value:
1-32 You can see from the positional values that usually fewer symbol positions are required to express a number in hex than in decimal. The following example shows this comparison:
62516 is equal to 157310
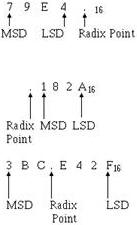
MSD and LSD
The most significant and least significant digits will be determined in the same manner as the other number systems. The following examples show the MSD and LSD of whole, fractional, and mixed hex numbers:
Addition of Hex Numbers
The addition of hex numbers may seem intimidating at first glance, but it is no different than addition in any other number system. The same rules apply. Certain combinations of symbols produce a carry while others do not. Some numerals combine to produce a sum represented by a letter. After a little practice you will be as confident adding hex numbers as you are adding decimal numbers.
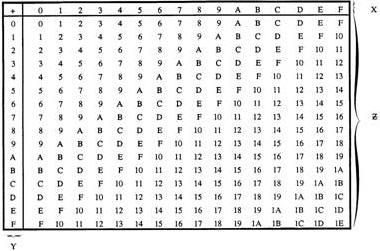
Study the hex addition table in table 1-6. Using the table, add 7 and 7. Locate the number 7 in both columns X and Y. The point in area Z where these two columns intersect is the sum; in this case 7 + 7 = E. As long as the sum of two numbers is 1510 or less, only one symbol is used for the sum. a carry will be produced when the sum of two numbers is 1610 or greater, as in the following examples:
1-33
Table 1-6. - Hexadecimal Addition Table
Use the addition table and follow the solution of the following problems:
In this example each column is straight addition with no carry.
Now add the addend (78416) and the sum (BDA16) of the previous problem:
Here the sum of 4 and a is E. Adding 8 and D is 1516; write down 5 and carry a 1. Add the first carry to the 7 in the next column and add the sum, 8, to B. The result is 1316; write down 3 and carry a 1. Since only the last carry is left to add, bring it down to complete the problem.
Now observe the procedures for a more complex addition problem. You may find it easier to add the Arabic numerals in each column first:
1-34
The sum of 4, E, 1, and 3 in the first column is 1616. Write down the 6 and the carry. In the second column, 1, 1, 9, and 7 equals 1216. Write the carry over the next column. Add B and 2 - the sum is D. Write this in the sum line. Now add the final column, 1, 1, 5, and C. The sum is 1316. Write down the carry; then add 3 and B - the sum is E. Write down the E and bring down the final carry to complete the problem.
Now solve the following addition problems:
Q36. Add:
Q37. Add:
Q38. Add:
Q39. Add:
Q40. Add:
1-35 Q41. Add:
Subtraction of Hex Numbers
The subtraction of hex numbers looks more difficult than it really is. In the preceding sections you learned all the rules for subtraction. Now you need only to apply those rules to a new number system. The symbols may be different and the amount of the borrow is different, but the rules remain the same.
Use the hex addition table (table 1-6) to follow the solution of the following problems:
Working from left to right, first locate the subtrahend (2) in column Y. Follow this line across area Z until you reach C. The difference is located in column X directly above the C - in this case A. use this same procedure to reach the solution:
Now examine the following solutions:
In the previous example, when F was subtracted from 1E, a borrow was used. Since you cannot subtract F from E and have a positive difference, a borrow of 1016 was taken from the next higher value column. The borrow was added to E, and the higher value column was reduced by 1.
The following example shows the use of the borrow in a more difficult problem:
1-36
In this first step, B cannot be subtracted from 7, so you take a borrow of 1016 from the next higher value column. Add the borrow to the 7 in the minuend; then subtract (1716 minus B16 equals C16). Reduce the number from which the borrow was taken (3) by 1.
To subtract 416 from 216 also requires a borrow, as shown below:
Borrow 1016 from the a and reduce the minuend by 1. Add the borrow to the 2 and subtract 416 from 1216. The difference is E.
When solved the problem looks like this:
Remember that the borrow is 1016 not 1010.
There may be times when you need to borrow from a column that has a 0 in the minuend. In that case, you borrow from the next highest value column, which will provide you with a value in the 0 column that you can borrow from.
To subtract a from 7, you must borrow. To borrow you must first borrow from the 2. The 0 becomes 1016, which can give up a borrow. Reduce the 1016 by 1 to provide a borrow for the 7. Reducing 1016 by 1 equals F. Subtracting A16 from 1716 gives you D16. Bring down the 1 and F for a difference of 1FD16.
Now let's practice what we've learned by solving the following hex subtraction problems:
1-37
Q42. Subtract:
Q43. Subtract:
Q44. Subtract:
Q45. Subtract:
Q46. Subtract:
Q47. Subtract:
CONVERSION of BaseS
We mentioned in the introduction to this chapter that digital computers operate on electrical pulses. These pulses or the absence of, are easily represented by binary numbers. a pulse can represent a binary 1, and the lack of a pulse can represent a binary 0 or vice versa.
1-38 The sections of this chapter that discussed octal and hex numbers both mentioned that their number systems were beneficial to programmers. You will see later in this section that octal and hex numbers are easily converted to binary numbers and vice versa..
If you are going to work with computers, there will be many times when it will be necessary to convert decimal numbers to binary, octal, and hex numbers. You will also have to be able to convert binary, octal, and hex numbers to decimal numbers. Converting each number system to each of the others will be explained. This will prepare you for converting from any base to any other base when needed.
DECIMAL CONVERSION
Some computer systems have the capability to convert decimal numbers to binary numbers. They do this by using additional circuitry. Many of these systems require that the decimal numbers be converted to another form before entry.
Decimal to Binary
Conversion of a decimal number to any other base is accomplished by dividing the decimal number by the radix of the system you are converting to. The following definitions identify the basic terms used in division:
· QUOTIENT - The number resulting from the division of one number by another
To convert a base 10 whole number to its binary equivalent, first set up the problem for division:
Step 1 - Divide the base 10 number by the radix (2) of the binary system and extract the remainder (this becomes the binary number's LSD).
Step 2 - Continue the division by dividing the quotient of step 1 by the radix (2
1-39 Step 3 - Continue dividing quotients by the radix until the quotient becomes smaller that the divisor; then do one more division. The remainder is our MSD.
The remainder in step 1 is our LSD. Now rewrite the solution, and you will see that 510 equals 1012. Now follow the conversion of 2310 to binary:
Step 1 - Set up the problem for division:
Step 2 - Divide the number and extract the remainder:
1-40
|
||||||||||||||||||||||||||||||||||||||||||||||||||