Resistive Attenuators and Pads
May 1966 Electronics World

May 1966 Electronics World Table of Contents Wax nostalgic about and learn from the history of early electronics. See articles from Electronics World, published May 1959 - December 1971. All copyrights hereby acknowledged.

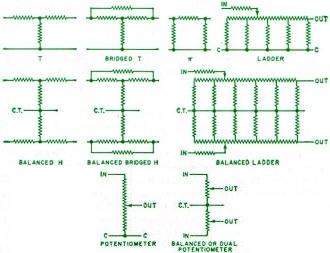
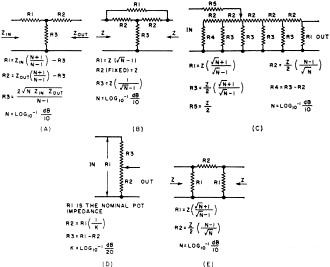
Here is a real cornucopia of attenuator information from the May 1966 issue of Electronics World magazine. If you need circuits diagram and equations for "T," Bridged-T, Ladder, Pi, Balanced-H, Balanced Ladder, Potentiometer, and Balanced (Dual) Potentiometer type attenuators, then you've come to the right place. A discussion is included on attenuator selection and specification for ordering rather than designing and building your own. The distinction between a "pad" and an "attenuator" has always been vague to me and I, like most people, use the terms interchangeably. Author Chester Scott seems to believe a "pad" always has a fixed value whereas an attenuator can be either fixed or variable.

Here is an article on resistive pads from a 1959 issue of Electronics World.

Resistive Attenuators and Pads

Circuitry, design, and selection of these devices which vary signal levels without disturbing the impedance, frequency response, or other system characteristics.

By Chester F. Scott

Chief Engineer

Daven Division, McGraw-Edison Co.

This article covers the circuitry and design of resistive attenuator networks. These are used to vary signal levels without disturbing the impedance, frequency response, or other characteristics of the system. They are referred to by many names such as faders, pads, mixers, masters, pots, etc., but the basic function remains the same.

Attenuator Classifications

Attenuators are divided into two main classifications: fixed and variable. Fixed attenuators are used where the level of a signal must be reduced by a known number of decibels which will not have to be changed. Variable attenuators are used where rapid or frequent changes in signal level are required. They are also used when the required amount of signal reduction must be determined at the time of system installation. Where frequent variations in level are necessary, an attenuator which is variable by a rotary or a straight-line switch is used. When the level can be adjusted and set with a minimum of future changes, a type that is variable by means of soldered interconnections is normally used.

The basic circuits for both the variable and fixed types are the same and the formulas for resistor values are equally applicable to both. In variable attenuators which are controlled by a switch, the variation is generally accomplished by adding or subtracting resistors in the series and shunt circuits. The exceptions are the ladder and π types. In the ladder type, all resistors are fixed and the series resistor tapped at correct intervals. The π operation is covered later. (Inexpensive variable attenuators are also available in which the various series and shunt elements consist of volume-control-type potentiometers that are ganged together to produce the proper resistance changes as the control is operated - Ed.) Attenuators that are variable by means of changing soldered interconnections consist of a group of fixed pads with different attenuations. The attenuation variation is accomplished by connecting attenuators with the correct losses in series to provide the required total attenuation.

Electrically, attenuators are divided into two main classifications: balanced and unbalanced. A balanced attenuator control is one where equal resistance is inserted in each side of the circuit and where the center point of any shunt resistance can be grounded or left floating depending upon the other circuit characteristics. An unbalanced control is one where the resistance is added in only one side of the line and where the other side of the line is "common" or grounded.  

In designing the equipment where attenuators are to be used, there are two schools of thought as to whether balanced or unbalanced controls are more satisfactory. One group claims that balanced circuitry is better because hum and noise due to ground loops and improper grounding is done away with. The other group contends that unbalanced circuitry is better because, with proper grounding, stray capacities are overcome and better control is obtained. This article will not attempt to deal with the merits of over-all system design. There are instances where economics will be a determining factor in system design, and we will only indicate that balanced controls are usually approximately twice as expensive as their unbalanced counterpart since twice the number of resistors and twice the switch facility are required.

An unbalanced control cannot be used where other circuitry is balanced because, to operate correctly throughout the required frequency range, an unbalanced control must have one side of the line grounded. A balanced control cannot be used in an unbalanced circuit since ground on one side of the unbalanced circuit would affect the control operation. One-half of a balanced control, i.e., one input terminal, one output terminal, and the center-tap terminal, can be employed in an unbalanced circuit but only if the particular circuit impedance is one-half that of the balanced control.

The most frequently used attenuator circuits are the T, bridged-T, ladder, and potentiometer types or their balanced counterparts, the balanced-H, balanced bridged-H, balanced ladder, and dual or balanced potentiometers. In high-frequency applications, the unbalanced π type is most generally used. The schematic diagrams for these types are shown in Fig. 1.

The following information covering the design and use of the various styles is given for the unbalanced types only. The formulas for determining the resistance values in a balanced control are the same as those indicated for the unbalanced control except that, in inserting the value for Z in the formula, the full value is used for an unbalanced control but only one-half the value is used for the balanced control. Thus, in determining the values for a 600-ohm attenuator, the value for Z in the formulas for an unbalanced control is 600 ohms, but that for a balanced control is 300 ohms.

The T attenuator is generally the most stable and, within reasonable limits of terminal impedance and range of attenuation, can be made the most accurate through fairly wide frequency ranges. Since it requires three variable resistors and their associated switching, it is generally the most expensive of the unbalanced types used at frequencies up to 1 MHz. Both the input and output impedances remain constant, within the specified resistor accuracy, throughout the attenuation range. The insertion loss of this type control is zero dB when the input and output impedances are equal.

These characteristics make the T attenuator especially useful as controls in instruments and other applications where accuracy and constant impedance are required. The formulas for determining the resistance values required are shown in Fig. 2A.

Where equal input and output impedances are involved, Z_in and Z_out are equal and the resulting values for R1 and R2 are also equal. For a fixed-loss attenuator with either equal or unequal input and output impedance, and for a variable loss attenuator with equal input and output impedance, the formulas are used without further consideration. For a variable loss attenuator with unequal input and output impedance, the resistor values are normally determined for one impedance, and an impedance-matching network is used to match the impedance at the other end. The resistance values for this impedance-matching network are determined as indicated later in this article.

The bridged-T network is a variation of the T network which requires the use of only two variable resistors. It is thus somewhat less expensive than the T but has practically equal characteristics up to somewhat lower attenuation values. The bridged-T has a constant input and output impedance throughout the attenuation range and has a zero dB insertion loss when the input and output impedances are equal. In the higher losses above 30 to 40 dB, the value for R1 (see Fig. 2B) becomes so high that it is more susceptible to the effect of any stray capacitance across it.

The bridged-T attenuator is normally used only for attenuators which are variable by means of rotary or linear switching. They are normally used between equal input and output impedances but, with the use of an impedance-matching network at one end, they can be used between unequal impedances with the necessary insertion loss due to the impedance match. They are used mainly in instruments or in communications equipment where constant impedance and zero insertion loss is important and where the attenuation range is not too great. The formulas for determining resistance values are shown in Fig. 2B.

Ladder Attenuators

The ladder type attenuator is actually a variation of the π type and is used only in the variable loss styles. It requires the use of only one variable resistor and is the least expensive of all the types except the potentiometer. Ladder attenuators are most generally used as mixer controls in public address systems and broadcast consoles, and also as controls in audiometers.

The circuitry is such that the output impedance falls to about two-thirds of the nominal value at the low loss end and the input impedance falls to approximately the same amount at the high attenuation end. The curves for a 30-step, 1 1/2 dB/step ladder with a 600-ohm input and output impedance are shown in Fig. 3. Throughout the mid-attenuation range, where the control is normally operated in mixing applications, both the input and output impedance are fairly constant and practically nominal.

The resistor values in a ladder attenuator are such that they remain within practical limits throughout the attenuation range. Thus, the high attenuation values required for audiometer applications are obtainable in a single control. With an equal input and output impedance, the ladder attenuator has an insertion loss of 6 dB. This is partially due to the fact that, unlike a T or bridged-T attenuator, all the resistors of the ladder attenuator are in the circuit at all times and control is obtained by connecting to various taps on the series resistor by means of the switch. The remainder of the insertion loss is due to the fact that a resistor, equal in value to one-half of the input impedance, is connected in series with the input to provide a more constant impedance. When the input impedance of a ladder attenuator is one-half of the output impedance, the resistor in series with the input is omitted and the insertion loss is approximately 2dB.

The ladder attenuator is unique because its circuit is such that any possible switching noise is attenuated along with the signal. This feature is helpful in mixer applications where the signal-to-noise ratio is especially important. The formulas for the resistor values in the ladder attenuator are shown in Fig. 2C.

For optimum decibel and impedance accuracy, dB in the formula is normally selected as 6 dB. For a 2 dB per step control, R2 is tapped for three equal sections and for 1 1/2 dB per step it is tapped for four equal sections.

Potentiometers and π Networks

The potentiometer is a simple potential divider and is designed to operate into a very high impedance such as the grid circuit of a vacuum-tube amplifier. It is used to control voltage in specific decibel steps or in special voltage ratio steps. It has the simplest construction and is therefore the least expensive of any of the attenuators. The formulas for determining the resistor values for this attenuator are shown in Fig. 2D.

The formulas are for potentiometers calibrated in decibel steps. When voltage ratios are required, the ratio of R2 to R1 is the same as the ratio of the required output voltage to the input voltage. Again, R3 = R1 - R2.

The π network is comparable to the T network in stability and accuracy. It is also a network which requires three variable resistors. It is not generally used in low- and medium-frequency variable attenuator applications because the switching is somewhat more complicated than that for the T network. It is more generally used in high-frequency attenuators because it is easier to shield and the resistor values are in a range more readily adaptable for the lower impedances used.

In the high-frequency variable attenuators, the variation in attenuation is accomplished by switching π attenuators of the correct loss in and out of the circuit. For this type of switching, the resistors values in a π network remain within a range which is not overly affected by stray capacitance. The formulas for the π network are shown in Fig. 2E.

Attenuation Per Step & Matching

The selection of the dB per step of any attenuator depends upon the usage. For controls used in instruments, the dB per step can be any value up to 10 dB, and sometimes more, depending upon the instrument requirements. In broadcast and recording operations, the normal maximum dB per step is 2.

In the higher quality recordings, no switching noise can be tolerated. If the dB per step is too high, there will be a noticeable "pop" if the control is switched between steps during a sustained note. The lower the dB per step, the more steps are required to obtain a comparable total attenuation and more steps means higher cost. Thus, economics enters into the choice, but in recording applications, steps of 1.5 dB or less, if practical, are commonly used.

For optimum over-all operation, the impedance of all portions of a system should match. Thus, with the exception of the potentiometer, the input impedance of the attenuator should equal the impedance of the source and the output impedance of the attenuator should be equal to that of the load.

When the source and load impedances are unequal, a resistive network can be utilized to match them. This impedance-matching network is generally a T network or its counterpart, the balanced-H. Where a resistive network is used to match unequal impedances, some loss is necessary. The amount of this loss is dependent upon the ratio of the higher impedance to the lower impedance being matched.

Power & Impedance Available

The normal power dissipation of most attenuators is 0.5 or 0.6 watt continuous. Such attenuators will handle up to approximately 2.5 watts peak in audio circuits where the level fluctuates considerably. Attenuators with continuous power rating up to 20 watts and, in special cases, higher are available. Attenuators which have a low dB loss, such as decade T types with 10 steps of 0.1 dB per step, can be used in circuits where the wattage is considerably above the normal rating of the control. This is due to the fact that only a relatively small portion of the power is dissipated in the attenuator whereas most of the power is dissipated in the load.

In general, balanced-H, T, and ladder attenuators are available with impedances up to about 1000 or 2000 ohms. For special applications, controls with higher impedances are obtainable but attenuation and frequency ranges must be considered since internal capacitance and capacitance in the external wiring will have greater effect on the attenuator accuracy. The attenuators used in high-frequency applications generally have an impedance of 50, 52, 73, or 75 ohms. Attenuators with 93- and 125-ohm impedances can be made but, for a specified accuracy, the frequency range is limited by capacitance effects. Potentiometers normally are made with impedances in the range from 1000 ohms to 1 megohm. Lower impedances are available with a somewhat reduced attenuation range due to resistance values becoming too low for practical manufacture. Capacitance effect becomes a limiting factor for impedances over 1 megohm.

Attenuation & Frequency Range

The attenuation range available in an attenuator depends upon impedance, circuit type, and frequency range. In bridged-T and bridged balanced-H attenuators the variable series resistor becomes exceedingly high at the higher losses and the variable shunt resistor becomes too low for practical manufacture. Thus the highest loss normally supplied in the bridged-T and bridged balanced-H types is approximately 40 dB. This is not a firm figure because impedance and dB per step must be taken into consideration.

In T and balanced-H attenuators the limiting factor on the dB range is the resistor value between steps in both the series and the shunt arms.

At the higher losses these become too low for practical manufacture. The approximate maximum loss normally supplied in the T and balanced-H attenuators is 60 dB but here again the actual maximum depends upon impedance and dB per step.

In the above types the total attenuation range of a variable attenuator may be increased by combining two or more attenuators on the same shaft and connecting them in series. For example, a 100-dB attenuator can be made by connecting two 50-dB attenuators in series. In operation, the first group of steps varies the first 50 dB and the second group of steps varies the second 50 dB. Up to 50 dB, the attenuation is varied in one section while the second section remains at zero dB. Above 50 dB the first section remains at 50 dB while the second section inserts the remainder of the attenuation.

In ladder and balanced ladder attenuators the circuitry is such that the resistor values do not get too high or too low as loss is increased and therefore they are not a limiting factor in the dB range. Thus, in these types, attenuation ranges of somewhat over 100 dB are obtainable.

Attenuators are available covering the frequency range from d.c. to 10 GHz. So-called audio-frequency attenuators will operate satisfactorily up to at least 100 kHz and in some instances, depending upon the decibel range and impedance, much higher. Video-frequency attenuators generally operate at frequencies up to 10 MHz and radio-frequency attenuators cover the remainder of the range to 10 GHz.

Attenuator accuracy is dependent upon the accuracy of the resistors used in their construction. At audio frequencies, the attenuation accuracy is the same as the resistor accuracy. Thus, if resistors with a 5% accuracy are used, the attenuation will be within 5% of nominal. Actually the attenuation accuracy will probably be much closer than 5%.

Attenuators used in broadcasting and recording operations normally have a 5% accuracy while those used in instruments and in measuring applications generally have a 1% accuracy and frequently have tolerances as close as 0.1%. The higher frequency attenuators normally have the accuracy specified in dB through a range of operating frequencies. Since this accuracy depends upon the amount of loss, impedance, and frequency range, a general statement of available accuracies is not feasible. For these applications the manufacturer should be consulted before completing an equipment design.

With the exception of a few covering fixed high-frequency types and two or three covering attenuation networks (two or more attenuators connected in series and mounted in a portable case or on a relay rack panel), there are no MIL-Specs on attenuators. However, attenuators are available which will meet most of the military environmental requirements such as: temperature extremes, humidity, shock, vibration, and salt spray. For detailed information, the manufacturer should be consulted.

Attenuator Ordering Information

Most attenuator manufacturers have catalogues which show the electrical and mechanical specifications of their "standard" attenuators. When items are required which are not included in the catalogue, the information supplied to the manufacturer should be as complete as possible to avoid delay or misunderstanding. As much as possible of the following information should be included.

1. Complete electrical specifications including whether the attenuator is to be fixed or variable. If fixed, include type of circuit, decibel loss, impedance (both input and output), required accuracy, frequency range, and operating level (power).

If variable, include type of circuit, impedance (both input and output), required accuracy, frequency range, operating level (power), number of steps and dB per step, linear or tapered, are "off" or "cue" positions required? (both input and output terminated but no signal goes through).

2. Mechanical specifications. If fixed, include maximum physical size (if space is important), and type of terminals and connectors.

If variable, include physical size or manufacturer's basic type, with or without detents (indexing device), any required shaft deviations from manufacturer's standard, and type of terminals or connectors.

Finally, specify any military requirements which must be met.

Posted December 5, 2022
(updated from original post on 11/20/2014)