|
As shown in the equations
below, there are many different types of averages used in science and mathematics. The one that is probably the
most familiar is the Arithmetic Mean. Arithmetic Mean To calculate the arithmetic
mean with discrete random variables, add up all the terms, and then divide by the number of terms in the
distribution. This type of average is commonly called the "average". The mean of a statistical distribution with a
continuous random variable is the value of that random variable, formally denoted by the lowercase Greek letter mu
(µ). The area under the probability density function curve to the left of µ is the same as the area under the
curve to the right of µ (i.e., symmetry).
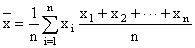 , n is an integer
Arithmetic Mean Formula
Median The median of a distribution with discrete random variables where the number of
terms is odd then uses the value of the term in the middle. This is the value such that the number of terms having
values greater than or equal to it is the same as the number of terms having values less than or equal to it. If
the number of terms is even, then the median is the average of the two terms in the middle, such that the number
of terms having values greater than or equal to it is the same as the number of terms having values less than or
equal to it. The median of a distribution with a continuous random variable is the value m such that the
probability is at least 0.5 (50%) that a randomly chosen point on the function will be less than or equal to m,
and the probability is at least 0.5 that a randomly chosen point on the function will be greater than or equal to
m. Discrete Random Variable vs. Continuous Random Variable
Since the definitions of Median, Mode, and Range all depend on whether the variables are discrete or continuous,
the difference is explained here for clarity. Discrete variables are a countable collection of values, e.g., the
numbers 2.2, 5.9, 2.0, 3.4, 6.2, 4.5. There are exactly six values. The mean for them is, per the above formula,
24.2/6 = 4.0(3). The actual result on a calculator is
4.0333333...., but since the precision of all the numbers in the set is two significant figures, the result has to
be the same. It has therefore been rounded down to 4.0. A continuous variable refers to a mathematical
function that takes on an infinite number of values between some lower and upper value. For instance, y = x2
[x=1→4] is the shape of a parabola and is defined for all
values of x between 1 and 4. Therefore, y take on an infinite number of values between 1 and 16. Arriving at the
answer requires using calculus to divide the integral of the range (x=1→4,
which results in the value of 63) by the range of x (which is 4-1 = 3), to get 63/9 = 7. The precision of the
range of x definition is one significant digit, so the answer is the same precision. In this case, even if the
range of x was defined as x=1.00000 to x = 4.00000, the answer would still be exactly 7 (7.00000) because the
ration 63/9 is exact.
Mode The mode of a distribution is the value of the term that occurs the most often. Often a
distribution will have more than one mode, especially if there are not many terms. This happens when two or more
terms occur with equal frequency, and more often than any of the others. A distribution with two modes is called
bimodal. A distribution with three modes is called trimodal. The mode of a distribution with a continuous random
variable is the maximum value of the function. As with discrete distributions, there may be more than one mode.
Range The range of a distribution with discrete random variables is the difference between
the maximum value and the minimum value. For a distribution with a continuous random variable, the range is the
difference between the two extreme points on the distribution curve, where the value of the function falls to
zero. For any value outside the range of a distribution, the value of the function is equal to 0.
Weighted Arithmetic Mean
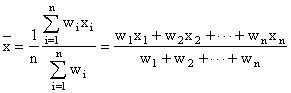
, n is an integer Weighted Arithmetic Mean
Geometric Mean
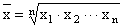
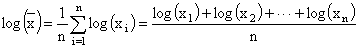 , n is an integer , n is an integer
Geometric Mean
Harmonic Mean
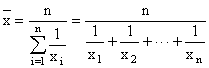 , n is an integer
Harmonic Mean
Root Mean Square (rms)
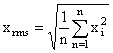
n is an integer Root Mean Square (rms)
|







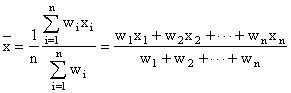
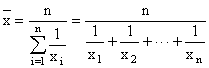 , n is an integer
, n is an integer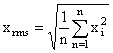 n is an integer
n is an integer