3-Dimensional Coordinate System Conversions

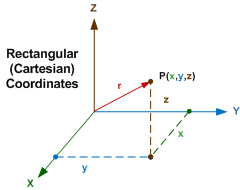
There are three fundamental three dimensional (3-D) coordinate systems (rectangular, cylindrical, and spherical), each of which is a more convenient means for calculations depending on the configuration of your model. For example, mapping points on the surface of a sphere using the Cartesian coordinate system requires describing all three coordinates (x, y, and z) in terms distance from each of the threes axis references. Doing the same in the spherical coordinate system requires simply a radius and two angles. When you start doing very complex calculations like those requiring calculus applications, choosing the best coordinate system can make the difference between nightmarish equations and relatively simple ones. Conversion formulas between the three fundamental coordinate systems are as follows. Note that N^½ = square root of N.

Rectangular to Cylindrical:

Given rectangular coordinates (x, y, z), convert to cylindrical coordinates (r, θ, z):

r = (x² + y²)^½

θ = tan^-1(y/x)

z = z

Rectangular to Spherical:

Given rectangular coordinates (x, y, z), convert to spherical coordinates (ρ, θ, Φ):

ρ = (x² + y² + z²)^½

θ = tan^-1(y/x)

Φ = cos^-1[z/(x² + y² + z²)]

Cylindrical to Rectangular:

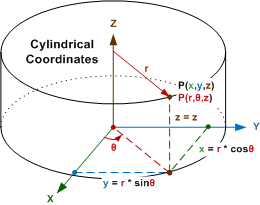
Given cylindrical coordinates (r, θ, z), convert to rectangular coordinates (x, y, z):

x = r * cos(θ)

y = r * sin(θ)

z = z

Spherical to Rectangular:

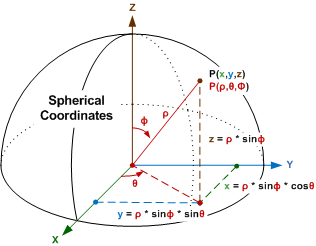
Given spherical coordinates (ρ, Φ, θ), convert to rectangular coordinates (x, y, z):

x = ρ * sin(Φ) * cos(θ)

y = ρ * sin(Φ) * sin(θ)

z = ρ * sin(Φ)

Spherical to Cylindrical:

Given spherical coordinates (ρ, θ, Φ), convert to cylindrical coordinates (r, θ, z):

r = ρ * sin(Φ)

θ = θ

z = ρ * cos(Φ)

Cylindrical to Spherical:

Given cylindrical coordinates (r, θ, z), convert to spherical coordinates (ρ, θ, Φ):

ρ = (r² + z²)^½

θ = θ

Φ = tan^-1(r/z)

Here is a convenient online coordinate system converter on the Random Science Tools and Calculators website.

Posted September 15, 2023
(updated from original post on 2/4/2009)