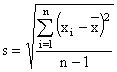|
In probability theory and
statistics, the variance of a random variable, probability distribution, or sample is a measure of statistical
dispersion, averaging the squared distance of its possible values from the expected value (mean). Whereas the mean
is a way to describe the location of a distribution, the variance is a way to capture its scale or degree of being
spread out. The unit of variance is the square of the unit of the original variable. The positive square root of
the variance, called the standard deviation, has the same units as the original variable and can be easier to
interpret for this reason. The variance of a real-valued random variable is its second central moment, and
it also happens to be its second cumulant. In statistics, standard deviation is a simple measure of the
variability or dispersion of a population, a data set, or a probability distribution. A low standard deviation
indicates that the data points tend to be very close to the same value (the mean), while high standard deviation
indicates that the data are “spread out” over a large range of values. -
Wikipedia
| Mean Deviation |
|
Standard Deviation |
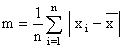 |
|
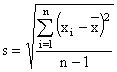 |
| where x is the mean of the sample, n is an
integer Variance is the square of the Standard Deviation = s2 |
|