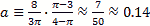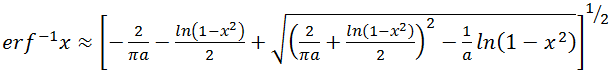|
Note: The error function and complementary function used in
communications are not exactly the same as the ones typically used in statistics.
The relationship between the two is given at the bottom of the page.
"In mathematics, the error function (also called the Gauss error function)
is a special function (non-elementary) of sigmoid shape which occurs in probability,
statistics, materials science, and partial differential equations."
- Wikipedia
The Gaussian probability density function with mean = 0 and variance =1 is
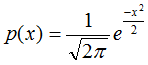
The error function erf(x) is defined as:
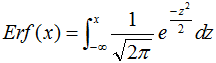
Note that erf(0) = 0.5, and that erf(∞)=1.
The complementary error function erfc(x) is defined as:
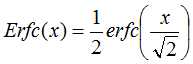
The following graph illustrates the region of the normal curve that is being
integrated. 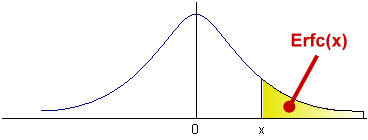
For large values of x (>3), the complementary error function can be approximated
by:
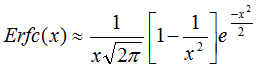
The error in the approximation is about -2% for x=3, and -1% for x=4, and gets
progressively better with larger values of x.
Approximations
RF Cafe visitor Ilya L. provided an approximation for the error function and
complementary error function that was published by
Sergei Winitzki titled, "A handy approximation for the error function and
its inverse," February 6, 2008 (Google Drive file - slow to load).
Here are the main results:
Error function approximation:
,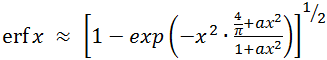 where where
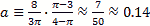
Complementary error function:
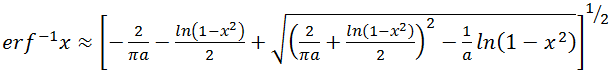
NOTE: I used to have an alternative approximation formula
for the complementary error function for large values of x, but decided to remove
it since the source for it is not generally available to the public. It can be found
as equation #13, on page 641, of
IEEE Transactions on Communications volume COM-27,
No. 3, dated March 1979. A subscription to the IEEE service is required to access
the article.
|








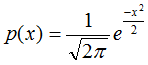
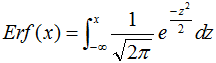
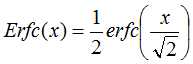

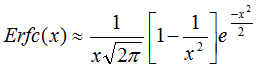
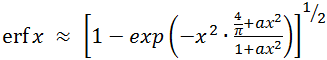 where
where