|
|
|||||||||
| Software: RF Cascade Workbook | RF Symbols for Office | RF Symbols & Stencils for Visio | Espresso Workbook | ||||||||||
|
|||||||||||||||||||||||||||||||
   |
  |
||||||||||||||||||||||||||||||
|
Please Support RF Cafe by purchasing my ridiculously low-priced products, all of which I created. RF & Electronics Symbols for Visio RF & Electronics Symbols for Office RF & Electronics Stencils for Visio T-Shirts, Mugs, Cups, Ball Caps, Mouse Pads These Are Available for Free |
|||||||||||||||||||||||||||||||
Rules of Exponents
The exponent is usually shown as a superscript to the right of the base. The exponentiation an can be read as: a raised to the n-th power, a raised to the power [of] n or possibly a raised to the exponent [of] n, or more briefly: a to the n-th power or a to the power [of] n, or even more briefly: a to the n. Some exponents have their own pronunciation: for example, a2 is usually read as a squared and a3 as a cubed.
The power an can be defined also when n is a negative integer, at least for nonzero a. No natural extension to all real a and n exists, but when the base a is a positive real number, an can be defined for all real and even complex exponents n via the exponential function ez. Trigonometric functions can be expressed in terms of complex exponentiation. - Wikipedia
| ax · ay = a (x+y) |  |
 |
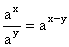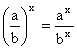| ( a · b )x = ax · bx | ||
| ( ax )y = a x·y | ||
 |
 |
 |
 |
 |
 |
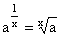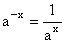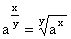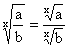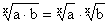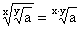Copyright: 1996 - 2026 |
About RF Cafe RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The World Wide Web (Internet) was largely an unknown entity at the time and bandwidth was a scarce commodity. Dial-up modems blazed along at 14.4 kbps while tying up your telephone line, and a lady's voice announced "You've Got Mail" when a new message arrived... |
Copyright 1996 - 2026 All trademarks, copyrights, patents, and other rights of ownership to images
and text used on the RF Cafe website are hereby acknowledge My Hobby Website: My Daughter's Website: |
