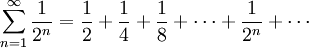everythingRF RF & Microwave Parts Database (h2) - RF Cafe

Series Expansions

In mathematics, given an infinite sequence of numbers {a_n}, a series is informally the result of adding all those terms together. These can be written more compactly using the summation symbol ∑. An example is the famous series from Zeno's Dichotomy:

$\sum_{n=1}^\infty \frac{1}{2^n} = \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+\cdots+ \frac{1}{2^n}+\cdots from Wikipedia - RF Cafe$

The terms of the series are often produced according to a certain rule, such as by a formula, by an algorithm, by a sequence of measurements, or even by a random number generator. As there are an infinite number of terms, this notion is often called an infinite series. Unlike finite summations, series need tools from mathematical analysis to be fully understood and manipulated. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics and computer science. - Wikipedia

Taylor's Series

Binomial Expansion

Exponential Expansion	Logarithmic Expansion

Sine Expansion	Cosine Expansion

θ expressed in radians




About RF Cafe
Copyright: 1996 - 2024 Webmaster: Kirt Blattenberger, BSEE - KB3UON
RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The Internet was still largely an unknown entity at the time and not much was available in the form of WYSIWYG ... All trademarks, copyrights, patents, and other rights of ownership to images and text used on the RF Cafe website are hereby acknowledged. My Hobby Website: AirplanesAndRockets.com