|
April 1972 Popular Electronics
 Table of Contents Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
Popular Electronics,
published October 1954 - April 1985. All copyrights are hereby acknowledged.
|
Whenever I read the April
issue of any magazine, vintage or contemporary, lurking in my mind is whether it
is an attempt at an April Fools "gotcha." The article title is usually the first
clue that the author is trying to punk me at least provides a sporting chance. Take
for instance this "Analog Logic" piece in the April 1972 edition of Popular
Electronics. It could easily be a hoax, so I proceeded cautiously. It turns
out to be completely legitimate. James Hannas provides a few examples of how analog
circuits can be used to perform mathematical functions that are easily handled by
logic circuits. Of course prior to the introduction of readily available, inexpensive
digital integrated circuits only a few years earlier, all those mathematical functions
were performed by analog circuits, so this was nothing new to most readers. If you
have never researched the capabilities of both analog and mechanical computers,
it would be worth your time; you will be amazed. One example that always impresses
me is the electromechanical systems that pointed and stabilized the massive
gun turrets on battleships during World War II.
Analog Logic: It Takes More Than Flip-Flops to Make a Calculator
By James Hannas
Have you ever wondered how some complex calculators can do so many operations
at such high speed and accuracy? The answer is in the use of linear and non-linear
integrated circuits that are basically quite simple in theory. Most of the circuits
involve an operational amplifier - a very high-gain linear amplifier that inverts
the input signal.
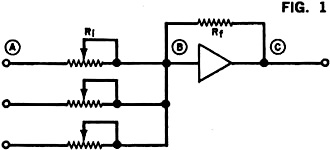
When input and feedback resistors are connected to the op amp as shown in Fig. 1,
the amplifier tries to maintain its input as close to zero as possible. The higher
the gain, the lower the offset or error voltage. To do this, the amplifier must
cause a current through the feedback and input so that the voltage drop across the
input resistor is equal to the input voltage. The input swing is equal to the input
voltage times Rf/Ri. A graphical analogy of the amplifier is shown
in Fig. 2.
Using the same circuit, but with additional input resistors, the amplifier can
be made into an adder. The sum of the voltages can also be multiplied by a constant
by adjusting the input resistors.
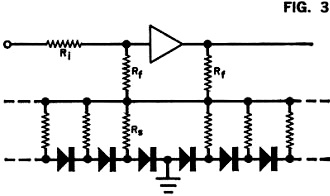
Nonlinear functions, such as squaring, can be performed by the diode shunt matrix
shown in Fig. 3. By adjusting the feedback resistors, any type of curve with
increasing magnitude can be formed. A logarithmic, or decreasing, curve will result
when the diode matrix is used as a feedback instead of a shunt matrix.
The most common squaring circuit is shown in Fig. 4. The numbers on the
op amps indicate the multiplier constants. By adding one quarter of the sums of
A-B and A+B, the result is the product of A and B.
Division is shown in Fig. 5. Here an op amp is supplied feedback by a multiplier
circuit which is controlled by B. As B increases, the output decreases.
There are also operational amplifiers and multipliers which are binary-to-analog
and analog-to-binary converters. These are basically resistor networks and amplifiers.
By combining analog circuits with binary bit storage, switching and readouts, a
compact calculator can be designed.
Posted March 2, 2023
(updated from original post on 12/19/2017)
|