Ohm's Law Quiz - How's Your E=IR?
March 1969 Popular Electronics

March 1969 Popular Electronics

March 1969 Popular Electronics Cover - RF CafeTable of Contents

Wax nostalgic about and learn from the history of early electronics. See articles from Popular Electronics, published October 1954 - April 1985. All copyrights are hereby acknowledged.

All but two of these circuits in this "How's Your E=IR? Quiz" can be analyzed by inspection, without even needing a calculator or writing down equations, because the component, voltage, and current values given are integer ratios that make the math easy. It appeared in a 1969 issue of Popular Electronics magazine. You might end up with an order-of-magnitude error when mentally calculating milli, kilo, etc., but your base number will be correct. Numbers 8 and 10 are a bit trickier. Your approach might be to rearrange the schematic to create more recognizable series and/or parallel component configurations. For number 8, I ended up writing equations for the three circuit loops and solving the simultaneous equations because I did not see the balanced bridge configuration at first (see at bottom of page). However, my mesh equations yielded I25Ω = 0 mA. Be careful with number 10 to not assume there is 10 volts across the unknown resistor.

How's Your E=IR ?

By Robert P. Balin

Ohm's Law Quiz - How's Your E=IR?, March 1969 Popular Electronics - RF CafeOhm's Law is the most valuable tool in electronics. It tells how voltage, current, and resistance are related to each other in a closed electrical loop. Test your knowledge of Ohm's Law in d.c. circuits by solving for the unknown voltage, current, or resistance in each of the ten circuits shown here. Assume that the meters have no effect on the circuits. Answers to quiz can be found on page 112 (see below).

 

 

Posted February 7, 2023

Quizzes from vintage electronics magazines such as Popular Electronics, Electronics-World, QST, and Radio News were published over the years - some really simple and others not so simple. Robert P. Balin created most of the quizzes for Popular Electronics. This is a listing of all I have posted thus far.

RF Cafe Quizzes

Vintage Electronics Magazine Quizzes

Vintage Electronics Magazine Quizzes

 

 

 

 

How's Your E=IR? Quiz Answers

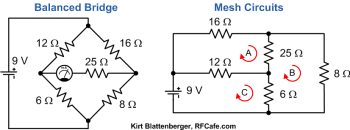
Circuit #8 re-drawn in familiar balanced bridge configuration (by Kirt Blattenberger, RFCafe.com) - RF Cafe

Circuit #8 re-drawn in familiar balanced bridge and in mesh equation configurations (by Kirt Blattenberger, RFCafe.com)

Mesh equations:  -53A+25B+12C=0
                               25A-39B+6C=0
                               12A+6B-18C=-9

A = 3/8 amp, B = 3/8 amp, C = 7/8 amp

Current through R25Ω = IA - IB = (3/8 - 3/8) amp = 0 amp

1. In a series circuit, voltage drops are directly proportional to the resistances across which they are measured: E1R1 = E2R2; E/5k = 8V/20k; E = 2V.

2. Current through a resistance is equal to the voltage drop across the resistance divided by the resistance value: I = E/R = 8V/2k = 4mA.

3. Total current flows through all components in a series circuit: I = E/R =- 20V/32k = 6.25mA; R = E/I = 5V/6.25mA = 8000 ohms.

4. Components that do not form a complete electrical loop have no voltage drop across them: E = IR = 2 mA*8k = 16V.

5. The currents in parallel branches are inversely proportional to the resistance in each branch: E1R1 = E2R2 = I(40 k) = (15 - I)160 k; I = 12 mA.

6. An unknown resistance is found by dividing the voltage drop across it by the current through it: R = E/I = 10V/2mA = 5000 ohms.

7. The voltage drop across a resistance is the product obtained by multiplying the total current through it by the resistance value: E = IR = 8 mA*(5k) = 40 V.

8. The voltage drop between the midpoints of a balanced bridge is zero; hence the current is also zero.

9. Voltage drops across parallel branches are all equal: E = IR = 10mA(100k) = 1000V; R = E/I =1000V/(50mA - 10mA) = 1000V/40mA = 25,000 ohms.

10. The sum of the voltage drops in a closed loop exactly equals the applied voltage: 50V + E5k, = 40V + E10k = Eapplied. Hence, E10k = 2(E5k); 50V + E5k = 40V + 2E5k; E5k = 10V; E = 40V - 10V = 30V.