After Class: Special Information on Radio, TV, Radar and Nucleonics
November 1958 Popular Electronics

November 1958 Popular Electronics Table of Contents Wax nostalgic about and learn from the history of early electronics. See articles from Popular Electronics, published October 1954 - April 1985. All copyrights are hereby acknowledged.

Decibels always have been and always will be a daunting subject to a lot of people. For electronics types, the issue of when to multiply the logarithm of the ratio by 10 or by 20 seems to be the biggest stumbling block. After many years of working with decibels, it becomes second nature. There are still instances, though, where I see seasoned engineers and technicians routinely confuse unreferenced decibel units (dB, the logarithm of a ratio) with logs of ratios referred to some base value (dBm, dBV, etc.). The bel unit was originally created to quantitatively assign changes in perceived levels of sound loudness to the human ear. This article touches briefly on the history and application of the bel.

After Class: Special Information on Radio, TV, Radar and Nucleonics

Understanding Decibels

The decibel is probably least understood unit in electronics. Ask what an ampere is and you'll get the answer, "It's a unit of current measurement." Ask for the definition of an ohm and, "It's the unit of electrical resistance," is your answer. Now try and get the straight information on what a decibel is. You'll go all around the circuit and back again, and still not have an understandable explanation.

Here's the big secret - a decibel is nothing more than a unit of comparison between two sound intensities or loudnesses.

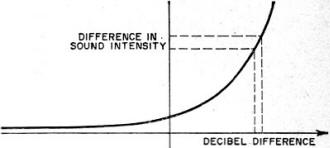
Sound Intensities. Back in the early 1920's, the telephone engineers were trying to measure the ability of the human ear to detect differences in sound intensity. It was a simple matter to measure a change in light intensity. The light became brighter and this change in brightness could be read off in foot-candles on a photocell.

Similarly, a change in temperature could be recorded on a thermometer in degrees. However, when a sound became louder, how would you measure that, and in what units? There was no unit available, so one was devised.

The unit for measuring sound levels was called the "bel" and was named in honor of the inventor of the telephone, Alexander Graham Bell. A decibel (db) is one tenth of a bel, this being a more practical unit with which to work.

Once again, the decibel is a unit of comparison of sound intensities. Comparison is the important word here. A decibel is not an absolute unit as is the volt, or ohm, or ampere.

The basis for this comparison of sounds is the ability of the human ear to detect a difference in loudness between two sounds. To put it another way, when your ear can just distinguish that one sound is louder than another, there is a difference of 1 db between the two sounds.

Human Reactance. Let's examine the way in which the human ear reacts to sound. Imagine you are visiting a dog show and fifty dogs are all barking at once. Loud, isn't it? Now imagine that fifty more dog fanciers arrive with their pets and that these fifty dogs all add to the din. Louder? Yes, but how much louder?

The sound intensity has doubled, but loud as it is, it doesn't sound twice as loud to your ear as the barking of the original fifty dogs. Not until five hundred dogs were all barking at once could your ear detect a sound twice as loud as the initial sound, that is, if you could stick it out that long.

Your ear responds to sound on what is known as a "logarithmic curve." Because of this, when the engineers were devising the equation for the comparison of two sound intensities they had to make it obey the same mathematical curve as did the logarithm. This curve is shown in Fig. 1. The decibel measurement, being a logarithmic function, gives a true picture of sounds as they affect the ear.

We will now relate what we have learned to decibel measurement in electronics.

Decibel Measurement. If we call the input power to an amplifier P_i and the output power from the amplifier P_o, and then express both quantities in watts, the formula for obtaining the number of decibels, N_db, gained through use of the amplifier is: N_db = 10 log P_o/P_i. Note that the logarithms used are to the base 10.

The steps in using this formula are:

1. Compute the ratio of Po/Pi expressed in watts.

2. Look up the value of the logarithm of this ratio in the log tables.

3. Multiply this logarithm by ten to get your answer in decibels.

Here is a practical example to illustrate the workings of this very important formula: If the input power to an amplifier is 0.2 watt and the output power of the amplifier is 10 watts, then:

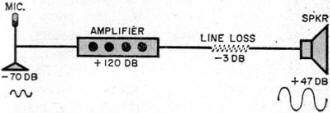
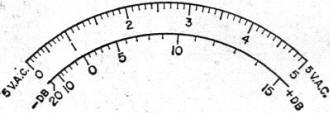
N_db = 10 log 10/0.2

N_db = 10 log 50

N_db = 10 x 1.70

N_db = 17 db

This shows that an increase of 50 times in the input power due to the amplifier action increases the power level of the output by 17 decibels. You can readily see that the decibel relationship compares the two powers, input and output, in the manner of their effect on the human ear when they are converted into sound.

Figure 2 shows, in block diagram form, one means of actually measuring decibels.

The amplification of any amplifier will vary according to the frequency being amplified. For that reason, amplifier ratings will show a figure such as, "Frequency response; ± 2 db, 20 to 20,000 cps." This indicates that the frequency of the input to the amplifier, when. varied over a range from 20 to 20,000 cps, will cause a variation in the output power of ± 2 db. The smaller this variation of output with change of frequency, the better the frequency response of the amplifier and the less distortion of the output.

If you are using two or more amplifiers in a circuit and want to know the overall rating of the system, you add the decibel rating of each one, assuming that the two units are perfectly matched. Decibels can be given as a minus (-db) figure indicating a loss as well as a plus (+db) figure indicating a gain. See Fig. 3.

Since the manufacturer of an amplifier does not know how it will be used in your system, he must establish some sort of zero reference point in order to figure a decibel rating for the particular unit under consideration. The zero levels generally used are 0.006 watt or 0.012 watt. These would represent the power input, or Pi in the formula we have discussed. There is also a standard impedance termination, or load, across which the output meter is connected in the measuring circuit. This value of load resistance must be the same for any comparative measurements.

Using a Meter. If you have occasion to use a direct-reading decibel meter, you will note that the scale spacing is uneven. This is due to the fact that the scale is laid out in logarithmic spacing rather than linear spacing which in turn is due to the logarithm in the decibel formula. A good example of the difference between a logarithmic scale and a linear scale can be seen by comparing the scales on a slide rule and on a ruler. The slide rule is logarithmic and he ruler is linear.

Actually, the output decibel meter is a d.c. voltmeter and rectifier combination. The meter measures output volts, but the scale reads in decibels. The zero point on the meter is that point on the scale where the zero reference level wattage is measured. Any reading over this zero point is read plus db, any reading below it, minus db.

It is important that you understand what decibels mean and what they tell you about the equipment you use. You will meet them often in your electronics work.