Standing Wave Ratio, December 1974 Popular Electronics

There is no such thing as too many articles on the subject of standing wave ratio. Standing waves were known and studied long before their behavior in transmission lines was of concern. Although the Wikipedia entry for standing waves credits Michael Faraday for first noticing them, undoubtedly centuries prior to that scientists like Archimedes, Isaac Newton, and Descartes observed and studied standing waves in ropes, vines, water, and other media. Author Carl Drumeller went into a fair amount of detail with his description of the phenomenon and the mathematical treatment of it, although he avoided the application of complex numbers lest he scare away those unfamiliar with them (a wise decision). This is one of the rare articles where voltage, current, and power standing wave descriptions are provided.

VSWR: What it is. How it affects communications. How and when to take corrective steps.

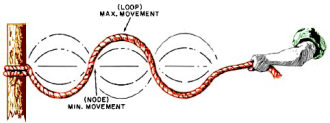
Fig. 1 - Standing waves on a rope. Such waves are generated by the combination of travelling waves headed in opposite directions.

SWR is a term used often in amateur and CB communications. Usually, it sounds as if the conversants were referring to an electromagnetic "bogeyman" which wreaks all manner of havoc in communications systems. Many strange powers are attributed to SWR, including the ability to destroy output tubes or transistors, make proper loading of transmitters difficult or impossible, neutralize a large portion of the output power, cause distortion, and even cause coaxial cable to heat up and melt its insulation.

Here's what SWR really is, how it affects communication systems and what can be done about it.

SWR is an abbreviation for Standing Wave Ratio, and comes in three varieties: Voltage Standing Wave Ratio (VSWR), Current Standing Wave Ratio (CSWR), and Power Standing Wave Ratio (PSWR). It is defined as the ratio of the maximum parameter (voltage, current, or power) to the minimum, when sampled along a length of transmission line. Why do waves "stand" on a line? Let us consider a typical transmitter installation.

The transmitter sends a train of sine waves down the transmission line (the radio "hose" which carries power toward the load). If the impedance of the antenna is the same as the output impedance of the transmitter and that of the line, then the impedance of the entire system is constant, and since V = I x Z (voltage equals current times impedance), the effective voltage and current are constant along the line, the maxima equal the minima, and the SWR is one, or as commonly said "one to one."

However, if the impedance of the antenna is different from the transmitter output impedance and that of the line, the wave train, which was "used" to the V = I x Z relationship of the line, experiences a new relationship at the abrupt change of impedance. In order to fit within the constraints of the laws electromagnetic waves obey, some of the power is sent back into the line, and a new wave train appears heading down the line toward the transmitter. When two waves headed in opposite directions meet, the result is a wave which stands still on the line. You can verify this with a simple experiment (see Fig. 1).

Tie a rope or string to some solid, stationary object (a tree or post will do). Grasp the free end and start waving the rope up and down. You are now generating a train of waves down the rope, much in the way that a transmitter sends waves down a transmission line. When the waves reach the point where the rope is anchored, they experience a new condition - the post can't allow them to propagate, since it is a stationary, inflexible object, so the waves are reflected and propagate back down the length of the rope. This situation is analogous to the termination of a transmission line with an impedance different from that of the line. You will see a wave appear on the rope that does not move. It is generated by the combination of the forward and reflected eaves, and is called a standing wave. The points on the rope that appear to be free of vibration are called nodes, and the points of maximum vibration are called loops or antinodes.

Fig. 2 - Voltage measured along a 50-ohm transmission line fed with 450 watts of 20-MHz r-f when connected to various loads. Voltage Standing Waves are generated when the line impednce is mismatched.

Fig. 3 - Typical SWR bridge installation. Bridge is placed in series with coaxial line along the way to the antenna at a convenient spot.

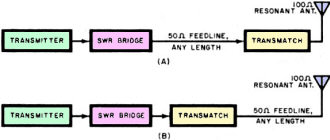
Fig. 4 - Transmatch configurations. Matching networks are adjusted to present a 50-ohm impedance to the transmitter. A mismatch can still appear at the antenna depending on where the transmatch is inserted.

When an impedance mismatch generates a standing wave on a line, the voltage and current distribution along the line is upset. In Fig. 2, we have plotted the voltage between the conductors of a transmission line as a function of the length of the line. A family of curves appears when various impedances are used to terminate the line. When Z_L (load impedance) is 50 ohms, we see that the effective value of the voltage along the line remains a constant 150 volts. This figure is determined by the equation P = V²/Z, where P is 450 watts and Z is 50 ohms. The maximum and minimum voltage (V_max and V_min) are both 150 volts, and the SWR, defined as V_max/V_min is 150V/150V, or 1:1 (Spoken as "one to one").

When a 25-ohm load terminates the line, a standing voltage wave appears on the line. V. equals 100 volts, and appears at the transmitter end of the line, and at integral multiples of one-half of a wavelength. V_max is 200 volts, and appears at odd multiples of one-quarter wavelength. The SWR is 200V/100V, or 2:1. When a 100-ohm load is connected to the line, the values of V_max and V_min are the same as the case above, except that the 200-volt V_max appears at the transmitter end of the line, and at whole multiples of a half-wavelength. V_max (100V) appears at odd multiples of a quarter-wavelength.

A more extreme case is shown when a 500-ohm load terminates the 50-ohm line. In this case, V_max equals 272 volts, and it appears at the transmitter end of the line. V_min, 27.2 volts, appears at odd multiples of a quarter-wavelength. The SWR is 272V/27.2V, or 10:1. We see that a large voltage is found at the transmitter-transmission line connection. This voltage may exceed the voltage rating of the active device(s) in direct-coupled final amplifier and destroy it. Transistors are much more intolerant of voltage overloads than tubes, and most will be destroyed instantly under such conditions. Even hardy vacuum tubes will blow when subjected to prolonged operation under these conditions.

If we terminate the line with a 5-ohm impedance, we note a V_min of 27.2 volts, at the transmitter feed point, and at integral multiples of a half - wavelength, and a V_max of 272 volts located at odd multiples of a quarter wavelength. As above, the SWR is 10:1.

High SWR will cause certain points along the transmission line to have a high r-f potential difference between conductors. In VHF or UHF systems, depending on the power rating of the cable, transmitter output power, and the SWR, this potential difference will be great enough to cause hot spots due to dielectric losses, or even arcing between conductors. Hot spots appear at current maxima in HF systems due to I²R effects. High SWR can make transmitter tuning very critical, necessitating large changes in control setting for a slight change in frequency. This occurs because the reactive effects of a mismatched line change with frequency, as does SWR.

Reactance, for the sake of review, is the opposition to ac offered by an inductance or capacitance. It is expressed in ohms, but is not a resistance - pure reactance does not dissipate any power, but returns a portion of the power to the generator during each cycle. A line not terminated in its characteristic impedance behaves in this manner by setting up a backward-travelling wave train. Equal amounts of capacitive and inductive reactance cancel each other out. For example, 25 ohms of inductive reactance combined with 25 ohms of capacitive reactance produce a net reactance of zero ohms.

The tuning and loading controls of a transmitter introduce amounts of inductive or capacitive reactance to cancel out the reactive properties of the line. If these adjustments are made correctly, the transmitter sees a purely resistive load. Impedance, the term we have used to describe the relationship between voltage and current in transmission lines and loads, is the phasor or vector sum of the resistance and reactance in a circuit.

If the characteristic impedance of the line (Z) and the impedance of the load (Z_L) are purely resistive, then the SWR may be obtained from: SWR = R_L/R_O for R_L>R_O and SWR = R_O/R_L for R_O> R_L. For example, if R_O is 50 ohms, and R_L is 25 ohms, the SWR is 50 ohms/25 ohms, or 2:1.

So far, we have not mentioned power loss as one of the seriously harmful effects of SWR on a communications system. Many operators look upon output power as a commodity more precious than gold, and develop ulcers at the thought of losing any of it to resistive or reactive elements in the system. While it is true that SWR indicates that a part of the transmitter output is not reaching the antenna, the amount of power lost in most situations does not justify the degree of concern it generates.

How can we determine what fraction of the power is being returned to the transmitter? A quantity called the reflection coefficient, ρ_r, gives this information. The reflection coefficient is defined as:

If a line has an SWR of 2:1, then the reflection coefficient is (2 - 1)/(2 +1), or 1/3. This means that 1/3 of the voltage wave sent down the line by the transmitter is returned. Since the power P equals V²/Z, the fraction of the power returned is equal to ρ_r², or 1/9. The portion of the power which is delivered to the antenna (neglecting line losses) may be expressed as the ratio of P, the power which reaches the load, to P_m the power which would reach the load if the system were matched, by the formula:

The power loss with a 2:1 SWR is not great (11% or ½ db). The human ear, or most S meters for that matter, could not tell the difference. Only when the SWR reaches 5:1 do we note a reflection of one half of the transmitter output power. This may sound like a large power loss, but it will only register as a 3-dB decrease in signal strength on an S meter. When such a meter is properly calibrated, one S unit equals 6 dB, so the decrease in signal strength caused by a 5:1 SWR will amount to only one half of an S unit. Many operators would be hard pressed to detect the differences using just their ears. However, as we have noted, this does not mean you should allow such a state of affairs to exist.

If, at a certain point along the transmission line, we sample the magnitude of the forward-going voltage wave, and then the reflected voltage wave, we can take the ratio of these magnitudes (forward to reflected) and obtain the VSWR. We could also sample power and obtain the PSWR. Devices which pass energy in only one direction are called directional couplers. An SWR monitor can be made by inserting two directional couplers into the line, and connecting them to meters which will monitor the magnitudes of the parameter we choose to measure.

There are many units available which will monitor SWR. The most common type is called a reflectometer or SWR bridge. Atypical reflectometer includes two jacks, to which cables from the transmitter output and the antenna are connected, a sensitive meter with a direct SWR scale calibration, a sensitivity control which is used to calibrate the unit, and a selector switch which connects the meter to one of two directional couplers. Prices of these reflectometers are usually $15 to $20, and the following comments pertain only to these types of reflectometers, not the more expensive, well engineered units.

Reflectometers of this type are adequate for most amateur and CB purposes, but there are a few realities that must be recognized before attempting to use one and obtain meaningful results. Reflectometers are designed to give a relative indication of SWR, but accuracy varies from unit to unit, and they are easily "fooled" into giving readings which do not truly reflect the conditions on the line.

If it were possible to connect the reflectometer to the line at any point (which is not convenient, since the line has to be interrupted to insert the reflectometer), we might get. a wide range of values of SWR from the meter. Does this mean that the SWR varies from point to point? No, it merely means that the line at certain points "hides" the true value of SWR from the reflectometer. If you already have an SWR Bridge, and have done some antenna experimentation, you might have encountered the following situation.

After installing a new antenna, a feedline is connected and run down to the transmitter. At the transmitter input, you connect the bridge and tune up the transmitter. After adjusting the bridge, you read an SWR of 1.5:1. Then, for one reason or another, you permanently move the transmitter and have to add on a piece of transmission line, or trim the line to fit the new operating location. The next time you tune up, you find you have an SWR of 3:1. "What's going on here?" you might wonder, since frequencies haven't changed or the antenna altered.

The answer to the higher SWR reading lies in the properties of a mismatched transmission line. Not only does a mismatch set up voltage, current and power standing waves, but an impedance one as well. If the mismatch is severe, but the transmission line is an odd multiple of a quarter-wavelength, the reactive effects of the line are hidden from the reflectometer and the transmitter (if the meter is inserted into the line close to the transmitter). In the first case, the line was close to this special length. But when the length was changed the true situation on the line was no longer hidden.

You may have noticed that some mobile antennas come with a length of transmission line attached, and the manufacturer's instructions clearly advise that the line not be cut, but that the excess be rolled up and stowed somewhere along the path the line will follow. This length is a quarter-wavelength or an odd multiple. Such antennas normally operate with a high SWR, but the length of the line is chosen to hide this from the transmitter. As you can see, you can't put absolute faith in a reflectometer reading.

There is an easy way to make sure that the SWR reading that the reflectometer is showing you is a close approximation of the actual SWR. Fig. 3 shows a typical installation configuration for a reflectometer.

The reflectometer may be inserted at any point along the transmission line, but as noted it may give different readings at various points. Which one is the true SWR? If the bridge is located at the antenna feed point, with the antenna connected directly to the output jack of the SWR bridge, then the reflectometer will indicate the true SWR on the line. This is an inconvenient place to connect the bridge, however, since most antennas are mounted a considerable distance away from the transmitting equipment, out of the operator's view.

Because of this difficulty, almost all SWR meters are inserted into the line near the transmitter or the operating position. If this is the case at your installation, you should connect a piece of transmission line, using a dual - female adapter and properly installed coaxial plugs between the line and the bridge. The extension should be less than Ye wavelength long. After installing the extension, tune up the transmitter (legally!) and note the SWR. If it has changed radically from the previous reading, you can be certain that a high SWR exists on the line and that any low readings are false. The test may also be run by trimming the feed-line, but usually this is inconvenient, since any cuts in the cable are permanent.

Now that you've made sure your SWR bridge is telling the truth and you find that you have an SWR of 3:1, what should be done? Should you fool around with the feedline or antenna or just leave things as they are? The answer depends on the type of feed line you have and the limitations of your transmitter.

If your transmitter is built to withstand "infinite SWR," then you can tolerate such a mismatch, and the power lost will not seriously degrade the strength of your signal. However, if you are using a transmitter which can take a maximum SWR of 2:1 (consult the spec sheet for this), and/or you are running an output close to the maximum power rating of the coaxial feedline, then you should take steps to make the mismatch less severe or make things appear that way.

Perhaps the easiest way to do this, if the load is highly reactive (a mini-whip or other loaded antenna), is to trim the length of coaxial feed line for a tolerable sending-end impedance. This does not really solve the mismatch problem, however.

The best way to correct a mismatch is to adjust the antenna or the feed line impedance for a good SWR. Most commonly available transceivers and transmitters are designed to work into 50- to 75 -ohm loads, and are tolerant of a maximum mismatch of 2:1. The range of impedances that the transceiver can work into is therefore from 25 to 150 ohms. If you are operating on one band only, 11 meters or one of the amateur bands between 7 and 30 MHz, you can use a simple dipole for edge-to-edge coverage. The maximum SWR should be 2:1, although it varies with the height above ground.

Most verticals can also cover an entire band with the same range of SWR. There is one trick to the successful operation of all vertical antennas. To obtain a decent SWR and efficient radiation, a good ground system must be used. If the vertical is roof-mounted, a radial system using at least five quarter-wave wires must be installed. The radials should droop slightly toward the roof.

A good radial system will include as many as 200 or more radial wires. Since copper wire is expensive these days, it is economically wise to use aluminum radials in your ground system.

By adjusting the radial system of a vertical, a dipole's height above ground, or a "gamma match" on a beam, you are changing the antenna feed-point impedance to a value which is closer to the characteristic impedance of the feed line, thus reducing the mismatch. This is the most effective way to reduce SWR.

There is another approach, however - matching networks or "transmatches." These devices act as variable impedance transformers, converting a wide range of loads to the ideal 52 ohms. Transmatches also tune out any reactance that the feedline may present to the transmitter, making it easier to load up the output stage. If a transmitter has a pi-network output, or a transmatch is used, SWR does not contribute to a power loss in the system. The network is adjusted to present the right amount of reactance necessary to cancel that at the load. Any power that is reflected down the line from the load will simply be rerouted back to the load. A forward-power measurement would show a greater amount than the transmitter output due to this compensation.

Figure 4 shows two configurations for transmatches. At "A" we see that a transmatch has been installed at the antenna end of a stretch of 50-ohm transmission line. A 100-ohm resonant antenna has been connected directly to the output of the transmatch: If we adjust the matching network to step down the 100-ohm impedance to a 50-ohm one, the SWR bridge will read 1:1. This is a true reading, since the transmitter output impedance, the line characteristic impedance, and the transformed antenna impedance are all 50 ohms. There are no standing waves on the line.

At "B" we have a second case. The transmatch is located at the transmitter end, right after the SWR bridge. Between the transmatch and the antenna, whose impedance is 100 ohms, a 50-ohm transmission line is connected. If we adjust the transmatch to give a 1:1 SWR reading on the reflectometer, do we have the perfectly matched condition at "A"? No, we don't! Although the transmatch fools the transmitter into thinking so, by presenting a 50-ohm impedance for the transmitter output, we still have an SWR on the transmission line due to the feeder/antenna mismatch.

When can SWR be ignored? If you are running output power well below the maximum rating of the feedline, and do not exceed the mismatch toleration of the transmitter, then you can safely ignore the SWR. If transmitter tuning becomes balky, feedlines heat up, or output amplifiers pop, then you should put into action one of the above -mentioned plans.

Try adjusting the antenna first. If you still have problems, make sure your transmission line and its connectors are in good shape. An antenna matcher should be used as a last resort (for coaxial lines). Above all, don't listen to the old wives' tales about SWR!

Standing Wave Ratio December 1974 Popular Electronics

Standing Wave Ratio
December 1974 Popular Electronics