|
July 1947 QST
 Table
of Contents Table
of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
Narrow-band frequency modulation (NFM) was
a relatively new technology in 1947, having been advanced significantly during World
War II. Amateur radio operators were just getting their gear back on the air
after having been prohibited from transmitting for the duration of the war
(see "War Comes," January
1942 QST). Few were probably thinking about adopting and exploiting
new modulation techniques, but for those who were and recognized FM as the path
to the future of radio, QST published this fairly comprehensive treatment
of both frequency modulation (FM) and phase modulation (PM). Mathematically, FM
is the time derivative of PM. Both modulation schemes vary the carrier frequency
in some proportion to the baseband signal. Author Byron Goodman provides some insight
into the techniques.
Low-Frequency N.F.M. and the Differences Between Frequency and
Phase Modulation
By Byron Goodman,* W1DX
F.m. and p.m. seem to be surrounded by more mystery than a.m. ever was. With
experimental bands soon to be available at 3.9 and 14.2 Mc., interest in the subject
should be increased considerably, so the following article is intended to clear
up some of the hazy points. A simple p.m. modulator is described for those who want
to get in on the ground floor.

Fig. 1 - Spectrum analysis of an a.m. signal. The unmodulated
carrier is shown at A, modulation by a single audio frequency is shown at B, and
modulation by two frequencies is represented in C. There is a single pair of sidebands
for each modulating frequency, and the sidebands are removed from the carrier by
that frequency.
Now that narrow-band frequency (and phase) modulation may soon be permitted in
portions of the 3.9- and 14-Mc. bands, this seems like a good time to look at some
of the points that have not been covered in recent issues of QST. There seem to
exist several popular misconceptions of just what the modulated carrier of an f.m.
or p.m. signal looks like and acts like, and it is the purpose of this article to
attempt to dispel these ideas and replace them with clearer pictures.
Everyone is familiar with pure amplitude modulation - a simple picture of the
distribution of energy in the spectrum of an a.m. signal is shown in Fig. 1.
The carrier frequency is represented by a single vertical line, as in 1-A. If the
carrier is modulated by a single frequency, F, of sufficient amplitude to produce
100% modulation, frequencies called "sidebands" are developed on either side of
the carrier, with an amplitude equal to one-half the carrier amplitude as in Fig. 1-B.
They are spaced in frequency from the carrier by the amount in cycles equal to the
modulating frequency, as indicated by + F and - F, relating to the carrier frequency.
If the modulating power is made up of a complex wave that can be resolved into two
frequencies, as in Fig. 1-C, sidebands occur for each of the two components
of the modulating frequency. Speech is a complex form that is practically always
made up of two or more frequencies. However, the important thing to remember about
a.m. is that for each modulation frequency, there exists a single pair of corresponding
sidebands, and no more. The simple representation in Fig. 1-C does not necessarily
take into account the relative phase of the modulating-frequency components, but
it is adequate to consider that the sideband amplitudes never exceed half the carrier
amplitude for 100% modulation. Further, when a sideband on one side of the carrier
is at a maximum, the corresponding sideband on 'the other side is also at maximum.
A simple phase-modulator unit that can be used to drive the average crystal-oscillator
stage. Receiving tubes are used throughout, and the output is about one watt. The
black shield houses one of the coils. Power plug and gain control are at the rear.
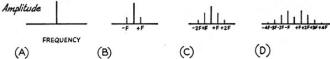
Fig. 2 - Spectrum analysis of an f.m. or p.m. signal. The
unmodulated carrier is shown at A, and modulation by a single frequency is shown
in B, C, and D. B corresponds ,to a low degree of modulation, C and D show what
takes place as the modulation is increased. All sidebands are spaced an amount equal
to the modulating frequency. Note that the amplitude of the carrier decreases as
the modulation is increased.
Frequency and phase modulation do not lend themselves to such simple pictures.
It is generally understood that frequency modulation is obtained by changing the
carrier frequency at the frequency of the modulation, and the greater the amplitude
of the modulation the greater the frequency change, or deviation, from the mean
carrier-frequency. Phase modulation, on the other hand, is obtained by shifting
the phase of the carrier frequency at the modulation frequency, and the greater
the amplitude of the modulation the greater the phase change. With a little thought
it can be seen that as the phase of the carrier is changed, by speeding up or slowing
down the r.f. alternations during the audio modulation cycle, the frequency of the
carrier must change at the same time, since more or fewer alternations than normal
must occur during the speeding-up or slowing-down process. Hence f.m. and p.m. are
similar in that the carrier frequency is changed during the modulation cycle.
Then it starts to get complicated! When a single tone is used to modulate a carrier
in either phase or frequency, not a single pair of sidebands results, as with a.m.,
but theoretically an infinite number of sidebands develops. The magnitude of the
sidebands depends upon the amplitude of modulation, with the sidebands close to
the carrier being the larger and the remote sidebands existing only theoretically
for all practical
purposes. To examine the procedure in an orderly fashion, assume a carrier modulated
by a single 1000-cycle tone. With very little modulation, only the first pair of
sidebands have any significant amplitude, and the picture looks similar to the one
for low-percentage amplitude modulation. As the degree of modulation is increased,
the second and third and higher-order sidebands begin to be significant, as shown
in Figs. 2-B, 2-C and 2-D. Notice that the sidebands occur at regular 1000-cycle
intervals. This is a significant point, since many seem to believe that f.m. (or
p.m.), can be made to occupy less spectrum space than a.m. by keeping the frequency
swing low. Such is not the case - the instant any modulation is applied to the carrier,
sidebands exist removed from the carrier by the modulation frequency. Fig. 3.
shows how the amplitude of the sidebands varies with the index of modulation - for
some degrees of modulation, some sidebands disappear and so does the carrier. Also,
some pairs of sidebands will be out of phase with each other for high degrees of
modulation.
Modulation Index

Fig. 3 - Showing how the amplitude of the sidebands of an
f.m. or p.m. signal varies as the modulation is increased. If the curves were extended
for greater values of "degree of modulation," it would be seen that the carrier
value goes through zero at several points, as do the various sidebands. Amateur
n.f.m. and n.p.m. should be confined to a degree of modulation equal to 0.5 or 0.6,
so the additional sidebands are not significant.
What we have elected to call "degree of modulation" in the above discussion is
more correctly known as the" modulation index." The modulation index is defined,
for f.m., as the ratio Δƒ/ƒ where Δƒ is the frequency deviation and F
the highest modulation frequency. For p.m., it is defined simply as the phase change,
in radians (one radian = 57.3 degrees). The curves in Fig. 3 apply to either
f.m. or p.m., if the modulation index as described above is substituted for "degree
of modulation."
The definition of modulation index helps to clarify the distinction between f.m.
and p.m. and how their audio characteristics differ when rectified by the same detector
system. In an f.m. system, for example, a modulation index of 2.0 means that the
maximum deviation divided by the highest modulation frequency is equal to 2.0. If
the top audio frequency is, for example, 5000 cycles, then the maximum deviation
will be ± 10 kc. The f.m. transmitter with an index of 2.0 and a top audio
frequency of 5000 cycles will deviate ± 10 kc. for full modulation at any
audio frequency below 5000 cycles. Any greater deviation doesn't mean "overmodulation"
as we know it for a.m., but simply that the signal can no longer be described as
having an index of 2.0. If the detection system is designed to give maximum output
for a deviation of ± 10 kc., then a greater deviation will result in distortion
in this detector, and it might be described as "overmodulation," but only for that
particular detector. Whether the modulating signal is 100 or 5000 cycles, maximum
undistorted output from the detector will be obtained when the deviation is ±
10 kc. in either case. Note that this represents a modulation index at 100 cycles
of 50. If Fig. 3 were extended to values of index ("degree of modulation"
in sketch) of 50, it would be found that the total number of significant sidebands
would be multiplied enormously. But with the modulation frequency of 100 cycles,
these sidebands are now only 100 cycles apart, and actually the significant sidebands
(less than 30 db. down) do not extend out as far as the fewer but more widely separated
sidebands of the 5000-cycle modulation frequency. It is therefore readily apparent
from the examples in this discussion that, with f.m., the modulation index gives
rather incomplete information on the bandwidth unless the highest audio frequency
is also specified.
In p.m. and any given modulation index, the number and amplitude of the sidebands
are exactly the same for any single modulation frequency, since the index in this
case is only the number of radians of phase swing either side of zero required to
give the phase modulation. However, the sidebands are separated by the modulation
frequency, so a low frequency of modulation will result in a narrow bandwidth and
a higher modulating frequency will cause the signal to occupy more spectrum space.
If the index is low (0.5 or less), so that only the first sidebands can be considered
as significant, this gives a spectrum picture quite similar to that for a.m. Fig. 4
illustrates the comparative spectrum space occupied by f.m. and p.m. signals for
different modulation indices and modulation frequencies. The p.m. pictures show
immediately why pure p.m. received on an f.m. detector will be lacking in "lows,"
since the f.m. detector requires that modulations of equal intensities but different
frequencies have roughly the same deviations. The condition can be corrected, of
course, by attenuation of the "highs" at the transmitter or receiver. The latter
is generally more convenient, since most receivers have a "tone" control that can
be cranked over to give the necessary attenuation of the higher frequencies.
One point worth noting about p.m. is the fact that it does not necessarily require
a long string of frequency multipliers following it in order to obtain a usable
index. Readers familiar with the Armstrong system of f.m. know that p.m. is used
at a low level and converted to f.m. Such a system does require considerable multiplication,
for reasons that will be described, but this is only because f.m. is the desired
end product. It is not impossible to obtain an index of 0.5 in p.m. without any
multiplication, and, indeed, this seems to hold the most promise for simple work
on the 75-meter band.
Reference to Fig. 5 will show why f.m. obtained by phase modulation requires
so much multiplication. For a p.m. signal, plotting deviation vs. modulating frequency
gives the solid line sloping up from the origin. Since f.m. requires nearly the
same deviation for all modulating frequencies, it is necessary to modify the audio
characteristic, as shown by the dotted line. This results in the f.m. characteristic
indicated by the dashed line, but note that it reduces the deviation to that obtainable
through p.m. at the lowest usable audio frequency. To minimize distortion, the phase
modulation is held down to a low level anyway, and the total result is a very low
modulation index at the control frequency. Such technique is not necessary in amateur
work, and hence p.m. looks good for our low-frequency bands. Phase modulation suffers
in its ability to reject noise, but this is not under discussion, although it is
of course a big point in the Armstrong system, and accounts for the use of f.m.
and a high index.
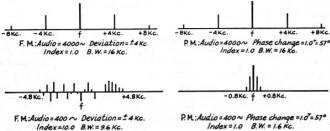
Fig. 4 - A comparison of the bandwidths of f.m. and p.m.
signals for different modulation frequencies. A modulation index of 1.0 and an upper
frequency limit of 4000 cycles are assumed. Note that the sketch for f.m. with an
index of 10 (lower left) shows the relative phase of the sidebands. Bandwidths are
based on neglecting sidebands down more than 30 db.

Fig. 5 - The necessary audio correction (dotted line) to
correct a p.m. characteristic (solid line) to f.m. (dash line). Note that this limits
the resultant f.m. deviation to the highest uncorrected p.m, deviation. This is
the principle used in wide-band f.m. transmitters, but it is not necessary for amateur
work.
It is important that one more point be clarified in this discussion. The pictures
given for single-tone f.m. or p.m. show a rather discouraging bandwidth for any
narrow-band application, if exactly the same condition were to hold for complex
modulation by two or more frequencies. However, when a complex wave is used to frequency
- or phase-modulate a carrier, the resulting sidebands are not the same as would
be obtained by superimposing the pictures of modulation by the component tones.
The existence of the side-bands in f.m. or p.m. always results in the reduction
of the carrier-frequency amplitude (see Figs. 2 and 3), and the total energy always
remains the same. If two sets of sidebands exist, corresponding to two modulation
frequencies, both of these sets of sidebands draw from the carrier, and the resultant
effect is to reduce the amplitude of the sidebands, since the carrier sets the limit
on total available energy. For this reason, a single audio frequency will yield
higher-order sidebands than will a complex wave of the same amplitude. This means
that a single tone applied to an f.m. or p.m. signal may show several sets of sidebands,
while voice modulation of the same amplitude will not show as many. As a result,
speech occupies less channel space than a single tone of the top frequency existing
in the speech for a given modulation index.2
Index Multiplication
Another point that is often confusing is what happens to f.m. and p.m. signals
at the harmonic frequencies of the carrier. At first glance, one might think that,
if a carrier is frequency-modulated at its fundamental by a 1000-cycle tone, to
give a pair of sidebands removed from the carrier by 1000 cycles, then the carrier
and the sidebands would have harmonics, and so the sidebands would move out from
the carrier at the harmonic frequencies. However, this is not the case, any more
than it is with a.m. Unfortunately, there is no simple physical picture that can
be given of the process of modulation of any type. We all know that sidebands are
generated under modulation, and it can be shown readily by mathematics that the
sidebands will appear. We can show the existence of the sidebands with a "spectrum
analyzer," but they just seem to be something we have to accept on the basis of
mathematical and practical proof. It isn't too many years since the "great sideband
controversy" raged between the English and American engineers, the English holding
that sidebands existed only in the mathematics.
The harmonics of the carrier result from distortion of the carrier in some nonlinear
element, such as a vacuum tube. But the sidebands are a result of the operation
performed on the carrier (a change in amplitude, frequency or phase). The change
of frequency or phase is multiplied in direct proportion to the frequency multiplication
generating the carrier harmonic frequency, but the sidebands set up are the same
as those produced by direct modulation of a carrier fundamental but with the greater
index of modulation. Hence in most f.m. and p.m. work it is customary to do the
modulation at a low frequency and frequency-multiply until the necessary index is
obtained.
Measuring Bandwidth
It will be necessary for any operator using narrow-band f.m. or p.m. to check
his transmissions and to be sure that his signal is occupying no more spectrum space
than an a.m. signal, in keeping with the definition of n.f.m. The future of f.m.
and p.m. in the amateur bands depends on those who use it during the trial period
and, since it is proving to be such a boon to those heckled by BCI, it would be
unwise and unfair to jeopardize its future by giving it a bad name on the air -
and with the FCC monitoring stations. For this reason, it is the duty of every user
of f.m. and p.m. to do his best to insure that his equipment is properly checked
and monitored. Unfortunately, this is not a simple problem, and no such clean-cut
solutions as exist for a.m. are known at the present time.
In the case of wide-band f.m., it is possible to apply single-tone modulation
and increase the modulation until the carrier disappears.3 This corresponds
to an index of 2.4 for the first disappearance of the carrier, and 5.5 for the second.
This is not a convenient method, however, for a station operating on 14 or 28 Mc.,
unless the operator has access to stable receiving equipment at 56 Mc. or some such
high harmonic frequency. One would then establish the audio level required to give
the necessary deviation, knowing that the index would be divided by the order of
multiplication, and then keep his modulation below this level, by means of a 'scope
or some other audio-level indicator. Figuring on an operating index of 0.6 at the
operating frequency, this method would require a 56-Mc. receiver to check a 14-Mc.
signal and a 112-Mc. receiver to check a 28-Mc. n.f.m. transmission, either one
with excellent frequency stability and good selectivity. A 3.9-Mc. signal can be
checked, of course, by a receiver capable of tuning to 15.6 Mc.
Another method, which is unfortunately beyond the reach of most amateurs, is
to use a special "spectrum analyzer" designed for n.f.m.
This is an instrument similar in principle to a panoramic receiver, but in this
case it requires a few refinements such as a crystal-filter i.f., a slow sweep rate,
and a long-persistence screen (to handle the slow sweep rate). Such a device would
make an excellent club project, but it is hardly likely to become standard ham-shack
gear. However, it is quite possible that it will be the sort of thing the FCC monitoring
stations will use for checking amateur n.f.m. transmissions, since it offers an
instantaneous picture of the bandwidth. This is no hardship on the n.f.m. gang,
however, because the same instrument turned on maladjusted a.m, signals would also
tell the sad story about them.
Since the precise methods are involved and expensive, we must fall back on something
a little more simple and less complicated. One redeeming feature of n.f.m. is that
one can listen to it as it will sound on the air without turning on the whole transmitter,
and this provides an excellent opportunity to do all the testing without putting
the signal into an antenna. By tuning in the harmonic of the n.f.m. unit on the
band where operation is to take place, one can get a rough check on the bandwidth
by noting how much room the signal takes in comparison with a.m. signals on the
same band. The most precise method available to the average amateur to measure the
bandwidth is to use his communications receiver and its crystal filter as a sort
of "poor man's spectrum analyzer." If the receiver is accurately calibrated in kilocycle
steps - which means that the absolute calibration can be off but the kilocycle divisions
accurate - or if a suitable calibration chart can be made to find out how many dial
divisions per kilocycle exist at the operating frequency, the problem is fairly
simple. The receiver must be stable, of course, and any measurements should only
be made after a suitable warm-up period. Suppose, for example, that one is setting
up his f.m. or p.m. signal in the 14-Mc. band. The oscillator and possibly one or
two following stages are turned on, to give a reasonable signal in the receiver
tuned to 20 meters. The signal level should be equivalent to an average signal in
the band, as judged by the S-meter, and it may be necessary to short the input of
the receiver to get it, unless the oscillator and other stages are operating at
a low power level. The receiver crystal filter is set to its sharpest position,
the b.f.o. is turned on and the a.v.c. turned off. It may be necessary to reduce
the r.f. gain slightly, to avoid overload of the receiver. Tune the carrier on the
peak of the crystal and set the b.f.o. for the usual beat note, around 500 or 600
cycles. If the receiver is accurately calibrated, either by the manufacturer or
by the operator making a calibration curve, detune it exactly 3 kc. If the calibration
isn't available, it will be necessary to modulate the f.m. or p.m. unit with a 3000-cycle
tone, which can be obtained from an audio oscillator built or borrowed for the occasion.
The 3000-cycle modulation will cause sidebands to appear on either side of the carrier,
spaced by 3000 cycles, and one of these will serve as a reference point. The amplitude
should be kept low, so as not to introduce more than one pair of detectable sidebands.
After the receiver setting is established 3 kc. off the carrier frequency, talking
into the microphone and experimenting with various voice levels will give some level
at which the voice is heard to splash over occasionally. This represents the upper
limit of modulation level that should be used. Once the proper level has been established,
it can be monitored by a 'scope or other voice-level indicator connected in the
audio amplifier ahead of the frequency or phase modulator, unless one is willing
to run the risk of depending upon the setting of the gain control and one's memory
of his voice level, bearing in mind his responsibility not to give n.f.m. a bad
name, or the FCC a chance to tag him. There is nothing simple that can indicate
directly from the carrier, as in a.m. work, since a properly-adjusted f.m. or p.m.
transmitter will be accompanied by no amplitude changes under modulation.
If the operator's voice is naturally high-pitched, the 3-kc. figure may be slightly
unfair, and perhaps 3.5 or even 4 kc. is a more reasonable limit. However, there
aren't very many necessary components existing in normal speech that run this high,
if there are any, and they are just as likely to be introduced by distortion in
the audio amplifier or modulator. The best practice, as in a.m., is probably to
limit the upper response of the audio amplifier to the useful frequencies below
3 or 3.5 kc., by means of suitable filters.
A Simple Phase Modulator
During the past few years, a number of different types of phase modulators have
been described in the literature. The new Raytheon cascade-modulation system is
interesting, but it requires a number of stages and the tuning procedure does not
lend itself too well to rapid frequency change, as is often required in amateur
work. Other systems using balanced modulators in one form or another are at a disadvantage
mainly because their apparent complexity will frighten a few potential customers
for p.m., although they are actually quite satisfactory in every respect.
One of the attractive things about p.m. is that it can be applied to the transmitter
at some point other than the oscillator, without any alterations that might impair
the frequency stability. Until we have quite accurate methods for measuring and
insuring bandwidth of f.m. transmissions, it seems highly desirable to avoid the
use of direct reactance modulation on the oscillator to obtain an f.m. signal. This
fact alone makes p.m. a natural for amateur use. Also, it is more difficult to obtain
a high index of modulation with p.m. than with f.m., so the bandwidth is inherently
more limited.
The simplest phase modulator we have been able to find is one suggested in Mr.
Hund's book.5 The author suggests using a reactance modulator across
the tuned plate circuit of a driven r.f. pentode amplifier. When the reactance modulator
changes the tuning of the circuit in accordance with the modulation, the phase angle
of the effective tuned circuit is changed and hence the phase of the voltage developed
across it. Since the phase change across a tuned circuit of Q = 10 or higher is
fairly linear for a range of ±25°, all that is required is a reactance modulator
capable of detuning the tuned circuit the necessary amount. Assuming a Q of 20 for
the circuit, an angle of 26.5° is obtained when the detuning is an amount equal
to 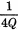 . This works out to be . This works out to be
 = 0.04875 Mc. = 50 kc.
approx. A Q of 20 will be obtained at 3.9 Mc. with a total tank capacity of 50 μμfd.
and an effective parallel resistance of 16,300 ohms (from Q = 2πƒRC). A
change of ± 1.2 μμfd. will swing the 50-μμfd. tank ± 50
kc., and this is easy to obtain with a reactance modulator. From the design equations,6
this can be obtained with a reactance modulator using an inductive element of 2.5
mh., a resistive element of 0.5 megohm and a mutual conductance change of ±
240 μmhos. This is a reasonable range for almost any of the better receiving-type
pentodes. = 0.04875 Mc. = 50 kc.
approx. A Q of 20 will be obtained at 3.9 Mc. with a total tank capacity of 50 μμfd.
and an effective parallel resistance of 16,300 ohms (from Q = 2πƒRC). A
change of ± 1.2 μμfd. will swing the 50-μμfd. tank ± 50
kc., and this is easy to obtain with a reactance modulator. From the design equations,6
this can be obtained with a reactance modulator using an inductive element of 2.5
mh., a resistive element of 0.5 megohm and a mutual conductance change of ±
240 μmhos. This is a reasonable range for almost any of the better receiving-type
pentodes.

Fig. 6 - A simple phase-modulator unit.

A view under the chassis of the phase modulator. The Tri-tet
cathode circuit is mounted on the side of the chassis near the microphone connector.
An experimental model was built and is shown in the photographs. The wiring diagram,
shown in Fig. 6, shows how simple the unit can be. A 6SJ7 speech amplifier
builds up the signal from a crystal microphone sufficiently to give enough swing
for the reactance modulator. A gain control, R5, allows the gain to be
reduced when the transmitter output is on 14 or 28 Mc., since the multiplied modulation
index at these frequencies might be too high. The reactance modulator is slightly
different than those previously described in that it uses an inductance-resistance
divider, RFC1R6, to obtain the quadrature current rather than
the more usual condenser-resistor combination. The principle, however, is practically
the same, and it requires no elaboration here.
A Tri-tet oscillator is used, with straight-through operation; i.e., the plate
circuit is tuned to the crystal frequency. Since this type of operation requires
a well-screened tube, the 6SK7 was selected. The effect is the same as if a separate
crystal-oscillator tube were used to drive an amplifier, since the plate-circuit
tuning or loading has no effect on the crystal oscillation. This is important if
one is to obtain pure phase modulation. If VFO were to be used, the VFO would feed
into a tuned circuit between grid and ground of the 6SK7, and the tuned cathode
circuit would be replaced by a bias resistor and by-pass condenser. In the unit
shown, the tuned cathode circuit is resonant around 4.5 Mc. Its tuning will affect
the amount of oscillator output slightly, but the major control of output is the
value of oscillator screen voltage. This was made convenient to adjust in the model
by bringing out the lead separately (marked "screen") and running it to the regulated
150 volts through an adjustable resistor. The value isn't critical, and several
fixed resistors are all that is necessary to make the adjustment. The oscillator
output must be adjusted to avoid overdriving the amplifier. The inductance L2
is shielded to avoid self-oscillation in the amplifier, and the plate by-pass condenser,
C16, is mounted across the tube socket to shield the grid and plate pins
from each other.
Since this particular unit is only a model and will probably not fit too well
into anyone's ideas about how such units should be constructed, only the tuning
details will be included. The operator with VFO can use the circuit by making the
oscillator changes mentioned earlier, and the station requiring more power output
from the unit will require additional power stages following the 6SG7 amplifier.
The output of this little unit is enough to light a small pilot lamp, representing
about one watt of power, enough to drive the usual crystal-oscillator stage. The
direct substitution of larger tubes throughout the unit is not recommended, unless
a well-shielded tube like the 802 is used, since one is likely to encounter the
usual difficulties with feed-back if beam tetrodes are used.
The first step in putting the unit in operation is to adjust the crystal oscillator.
With the screen of the oscillator connected directly to the 150-volt source, and
with normal voltages on the rest of the unit, adjust the cathode-circuit condenser,
C9, until the crystal oscillates. A 0-1 milliammeter between the bottom
of R11 and ground will serve as an output indicator, and a receiver should
be used as an additional check on the signal. When oscillation of the crystal has
been checked, add resistance in the oscillator screen lead until the grid-current
reading reaches a low value, of around 0.1 ma. or less. It should still be possible
to swing the tuning of C11 without throwing the crystal out of oscillation
or even affecting the frequency. If it can be thrown out of oscillation, readjust
C9 or reduce the value of the screen-dropping resistor. In the unit shown,
0.2 megohm could be connected in the screen lead without stopping crystal oscillation.
If a VFO is being fed into the unit, the screen voltage of the 6SK7 should be
reduced until the drive on the 6SG7 amplifier is as specified for crystal operation.
Using a small lamp load or the grid current of the stage the 6SG7 is driving,
resonate the output circuit L3C17. If it tunes broadly, it
probably indicates that the stage is being overdriven, or that the 6SG7 is oscillating,
although no trouble with oscillation was encountered in this unit. The modulated
circuit, L2C11, will tune broadly because it is loaded by
R11, but it should be centered on the broad resonance peak or otherwise
the modulation will fall off.
Talking into the microphone and monitoring the signal on 14 Mc. will give you
a check on the modulation, in the manner described earlier in this article. It will
be found that more than enough modulation can be obtained for 14 Mc. when using
an 80-meter crystal, but on 3.9 Mc. the best reception is obtained when using crystal-filter
reception methods, as outlined previously.7 For 3.9-Mc. work, it would
probably be better to do the modulating at 1.95 Mc.
No great claims are made for the unit, except that it is a simple thing to get
going and it will enable all of us that are interested to take advantage of the
opening of the lower-frequency bands to p.m. Somewhat greater swing can be obtained
by increasing the value of R11, and this might be necessary if a low-output
microphone is used. If listeners report "no lows," explain that you're using p.m.
and suggest that they crank up the tone control on their receivers. However, a cheap
crystal microphone may have poor low-frequency response, so the fault may be in
your own equipment if you are using a bargain microphone. Good practice would indicate
a low-pass filter ahead of the reactance modulator, to limit the high-frequency
response and consequently, the bandwidth, and such a filter could be put in the
circuit ahead of the gain control.
*Assistant Technical Editor, QST.
1 The information for these sketches and for Fig. 2 was obtained from Hund's
Frequency Modulation, McGraw-Hill Book Company, an excellent text for further study
of the subject.
2 Crosby, "Carrier and Side-Frequency Relations with Multi-Tone Frequency or
Phase Modulation," RCA Review, July, 1938.
3 Crosby. "A Method of Measuring Frequency Deviation." RCA Review, April, 1940;
also: Grammer, "Getting on 56-Mc. F.M.," QST, June, 1940.
4 Marks, "Cascade Phase-Shift Modulator," Electronibs, December, 1946.
5 See Footnote 1.
6 Hund, Frequency Modulation, p. 166.
7 Grammer, "N.F.M. Reception," QST March 1947
Posted September 15, 2021
(updated from original post on 6/11/2015)
|










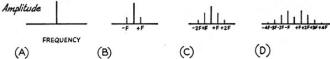



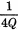 . This works out to be
. This works out to be
 = 0.04875 Mc. = 50 kc.
approx. A Q of 20 will be obtained at 3.9 Mc. with a total tank capacity of 50 μμfd.
and an effective parallel resistance of 16,300 ohms (from Q = 2
= 0.04875 Mc. = 50 kc.
approx. A Q of 20 will be obtained at 3.9 Mc. with a total tank capacity of 50 μμfd.
and an effective parallel resistance of 16,300 ohms (from Q = 2

