|
October 1953 Radio-Electronics
 [Table of Contents] [Table of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Electronics,
published 1930-1988. All copyrights hereby acknowledged.
|
An ability to interpret
the display on an oscilloscope is absolutely essential to efficiently diagnose a
circuit when troubleshooting. In the days of an electronics repair shop in every
town when televisions, radios, phonographs, tape recorders, and other consumer
gizmos were actually meant to be repaired rather than thrown away and replaced,
technicians needed to be able to compare a measured signal to the one
represented in the factory service manual, or what was known from experience to
be the expected signal. Especially with TV where complex analog broadcast
signals were decoded and routed to circuits for stereo audio, red, green and
blue color channels, scan synchronizations, and other functions, phase shifts
and signal distortion caused by any number of component failures or parameter
changes could be very difficult to troubleshoot. If you have read some of the "Mac's
Radio Service Shop" episodes, you have some idea of how valuable it was (is)
to be able to make an educated guess as to the cause of a signal anomaly as it
is traced through a circuit. This article provides a little insight into the
kind of knowledge required, and also is a good lesson for anyone working on
modern circuits - be they new designs or existing equipment being troubleshot or
modified.
Oscilloscope patterns enable complete amplifier analysis
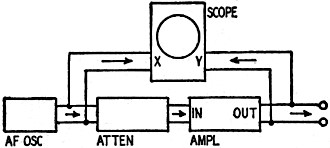
Fig. 1 - Simple hookup for diagnosing amplifier with oscilloscope
patterns.
By Norman H. Crowhurst
Magazine articles and textbooks often describe the use of oscilloscope patterns
to detect or assess amplifier distortion. The method, theoretically, is simple.
One merely connects the input of the amplifier to the X plates and the output to
the Y plates.
As generally presented in the literature, patterns show the effect of either
distortion or phase shift. In practice, distortion and phase shift frequently come
together, so a different pattern is produced.
Fig. 1 shows the general arrangement used for obtaining these patterns. Without
doubt, the method itself has advantages over either examining an oscilloscope trace
of input and output with an ordinary time-base (with or without electronic switching),
or analyzing input and output with a wave analyzer. For both methods, the input
should be almost a perfect sine wave.
For this method perfection of waveform is not so important - although the source
should be at least ostensibly a sine wave. Compared with the viewing of waveform
with an ordinary time-base, small degrees of distortion, particularly lower-order
harmonics, are easier to detect and identify.
The use of a wave analyzer identifies precisely the component frequencies produced
by distortion, but does not indicate how these component frequencies add up to modify
the waveform. To diagnose the cause of the distortion, the actual departure of the
waveform from its true shape is more helpful than a detailed analysis of the harmonics
introduced.
Phase Shift
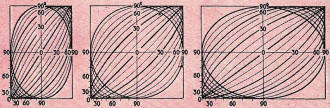
Fig. 2 - How phase shift shows up on scope, and how it may be
measured.
To make the whole matter quite clear, we will start by discussing phase shift
patterns when no distortion is present. Fig. 2 shows three families of phase-shift
ellipses. In each case zero phase shift is indicated by sloping line which means
that the spot traverses to and fro along the same trace. Introduction of phase shift
opens the line out into an ellipse, and when 90° is reached, the major and minor
axes of the ellipse are horizontal and vertical. Beyond 90° the ellipse would
tilt the opposite way, finishing up with a straight line sloping the opposite way
for 180° phase shift.
The three groups of Fig. 2 help clarify the significance of the mathematical
properties of various ellipses: In the center group the deflection due to the X
and Y plates is equal, so the zero phase shift line is at an angle of 45°, and
the 90° phase shift trace is a circle. The left and right groups of patterns
show the resulting pictures when the X deflection is less and greater than the Y
deflection respectively. It is most convenient for diagnosis to use the equal-deflection
pattern shown in the center of Fig. 2 if at all possible. In some instances this
may not be easy with the equipment available, so it is necessary to make out a pattern
on unequal X and Y deflections.
Ellipses are shown for 10° intervals of phase shift from zero to 90°,
and the 30° and 60° phase-shift ellipses are identified and distinguished
from the others by being drawn blacker.
Points by which to deduce the phase shift of any given ellipse are marked on
the figure. The best way to measure such an ellipse is to place a transparent cursor
with graph ruling in front of the oscilloscope and adjust both deflections so as
to fill an even number of squares. This provides a handy reference. Consider half
of one side of the square containing the pattern as equal to the unit "one." Using
this graphical unit of distance, the location of the points indicated (along the
left and bottom edges) is measured from the center or center line of the pattern.
Finding the Phase Angle
The point where the ellipse crosses the vertical or horizontal center line, measured
from the center of the pattern, is the sine of the phase-shift angle. (For example,
the 30° ellipse crosses the lines at 0.5 the length of the line.) The point on the
boundary square of the pattern where the ellipse touches it, measured along that
side from the center line, is the cosine of the phase shift angle. The cosine is
measured as a decimal fraction of the line, and the angle can then easily be found
by reference to a simple table of sines and cosines.
It is naturally easier to use the sine reference for angles between zero and
45° and the cosine reference for angles between 45° and 90°, but it
is a good idea to measure off both points as a check, particularly where the angle
lies between 30° and 60°. It is also a good plan to take an average of all
four possible reading points for each value, to eliminate any error due to the ellipse
not being quite correctly centered in its boundary square.
Distortion
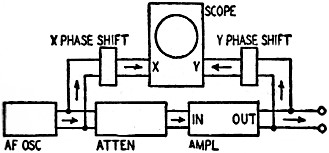
Fig. 3 - Setup for injecting phase shift into either X or Y plate
feed circuits.
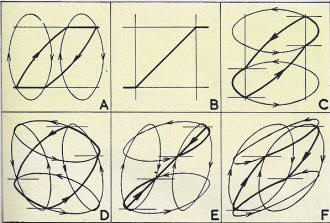
Fig. 4 - How a distorted trace's shape varies with phase shifts.
See text.
If the reader has tried to calibrate an oscillator with Lissajous patterns, as
described in the author's article in the November, 1952, issue of Radio-Electronics,
he will have noticed that when the patterns are not quite locked they appear to
be moving around. The direction of movement is somewhat subjective; that is, it
depends upon the imagination of the viewer at the moment. The movement could be
imagined as being due to a pattern traced on a transparent cylinder, which is rotated
on its axis so the pattern on the far side is viewed as if it were superimposed
on the pattern in front. The cylinder could equally well lie on a horizontal or
vertical axis, whereupon the movement due to its apparent rotation. It will appear
at right angles. If either of the patterns has a slight distortion, particularly
noticeable at one point in the waveform, the direction of the axis of rotation seems
to be identified by the movement of this distortion point. For example, if there
is a little kink in the 60-cycle waveform due to rectifier pulse current in a power-supply
unit connected to the same power line, this kink will maintain a regular position
horizontally, moving up and down along a vertical line in the trace, and the kink
will appear at all points in the pattern where it crosses this vertical line. This
will give the impression that the pattern is moving up and down vertically, or rotating
on a cylinder with a horizontal axis. On the other hand, if the output from the
oscillator has a similar definite distortion mark, the apparent movement will be
the opposite way, the distortion mark traveling along a definite horizontal line
in the pattern, as if the rotation were due to the pattern being traced on a cylinder
with a vertical axis.
All this is perhaps a little easier to visualize with Lissajous patterns where
the frequency applied to the two sets of plates differs. For our purpose the frequency
applied to both sets of plates is the same and the pattern does not move because
the phase difference remains constant. However, there are ways of making the pattern
move by introducing phase shift deliberately, and this can be an aid in recognizing
the particular form of distortion.
Fig. 3 shows that deliberate phase shift can be introduced into the signal fed
to the X plates or that to the Y plates. For practical purposes it is best to introduce
phase shift only into the undistorted signal fed to the X plates, because a phase-shift
network will alter the shape of waveform distortion, making it harder to recognize.
Fig. 4 shows the effect of phase shift applied in this way, together with construction
lines (representing our imaginary cylinder) to help visualize the movement of the
trace as phase shift takes place. The pattern at B shows the trace due to simple
distortion with no phase shift. This distortion could be due to grid current or
similar action producing clipping. The bent thick line can be regarded as an ellipse
viewed edge-on, with the ends bent over, rather like what might happen to the rim
of a bicycle wheel if it fell into a slot in the paving and the rider fell off the
bike sideways. The thin lines are construction lines to identify the position of
the sudden bends, and can be regarded as intersecting circles viewed edge-on.
The pattern shown at A is due to phase shift in the deflection of the X plates,
and C shows the effect of phase shift in the deflection of the Y plates only.
The remaining patterns, D, E, and F, show the effect of combined phase shift
on both sets of plates, maintaining the same phase shift in the Y-plate deflection
as that shown at C, which means that the points on the actual trace will move along
horizontal lines as the X shift is varied. To aid in visualizing this, horizontal
lines are drawn for the points where the curve suddenly changes, at C, D, E, and
F. To allow these points to move on a path similar to a point on the surface of
our imaginary vertical cylinder, the original construction lines, becoming ellipses,
move in the peculiar manner indicated at D, E, and F. The arrows on the ellipses
indicate an imaginary direction of rotation consistent with the arrows on the thick
line showing direction of spot movement. This direction is arbitrary and might easily
be in the opposite sense to the one shown.
At D the phase shift in both deflections is in opposite ways, so the resulting
pattern is more opened out. At E the two phase shifts are the same way and the same
amount, so, if no distortion were present, the straight line, due to the equivalent
ellipse being viewed edge-on, would be restored; but the bent-over portions are
now moved round so they appear as loops moving away from this straight line. F shows
the way the pattern distorts when the X phase shift is in the same direction as
the Y shift, but bigger, so as to turn the pattern inside out.
Some of these variations may occur in practical amplifiers. Phase shift may occur
before the distortion sets in and further phase shift may be introduced after the
paint of distortion. If the phase shift is due to the fact that the frequency of
the signal is either at the high or low end of the spectrum, it will be progressive,
all in the same direction, as the signal goes through the amplifier, before and
after the point where distortion occurs, but if viewed from the point of distention,
the earlier phase shift will be in the opposite direction from the shift after that
point (the signal on the X plates will be in advance of the point of distortion
and that on the Y plates behind it in phase.
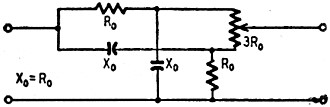
Fig. 5 - A simple phase-shift network.
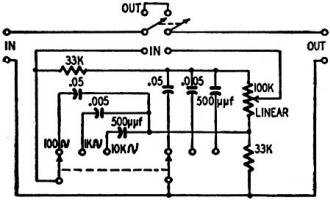
Fig. 6 - Three-frequency shift network.
So this combination would produce a pattern somewhat like that shown at D in
Fig. 4. Phase shift only before or after the distortion point would give an effect
similar to the trace shown at A or C respectively of Fig. 4.
To aid in recognizing patterns due to practical amplifier distortion, it may
therefore be helpful to inject deliberate phase shift into the signal fed to the
X plates. Fig. 5 shows a simple circuit that will give continuous phase shift variation
up to about 30° either way from the zero position. The capacitors are marked
in terms of their reactance at the frequency for which the network is used. Of course,
it can be used only at one frequency, or over a very limited range of frequencies,
with any particular set of values, but the arrangement could be modified by switching
in different capacitors to provide phase-shift facilities at different pre-set frequencies.
This type of network is used for phase shifting in many test instruments.
Fig. 6 shows the arrangement applied with switching for frequencies of 100, 1,000,
and 10,000 cycles. An extra switch is provided so the phase shift network can be
inserted or removed at will. This enables the frequency applied to the amplifier
to be swept through the frequency spectrum without deliberate phase shift, switching
over to the phase-shift arrangement at the preset frequencies of 100, 1,000, and
10,000 cycles for more detailed investigation of the pattern at these points.
Fig. 7 gives a complete set of prepared patterns for a variety of typical defects
in amplifier performance. The pattern for no phase shift is arranged in the second
column from the left-hand side for convenience - that for X phase shift only being
to the left, and that for Y phase shift only to the right of it. The remaining columns
give the effect of equal X and Y phase shift of 30°, the opposite way and the
same way. The kind of defect giving rise to the distortion is noted down the left
edge of the diagram.
The first four groups of patterns relate to clipping due to grid current or similar
action and curvature due to tube characteristics. The former may be due to inadequate
grid bias and the latter to too much grid bias. Wrong plate loading can also cause
these troubles. Some of the patterns show little difference between the two kinds
of distortion. Notice where the X and Y phase shift are the opposite way. Here the
difference between the two kinds of pattern is very small, and would be difficult
to identify on an actual trace; this means that if some phase shift occurred before
distortion, with some more phase shift after it, it would be difficult to determine
which of these two kinds of distortion were taking place. Introduction of phase
shift in the X plates to neutralize that in the amplifier before distortion occurs
would produce a pattern similar to that shown in Fig. 7, in the column "Y phase
shift 30°," where the difference between the two forms of distortion is quite
clearly identified.
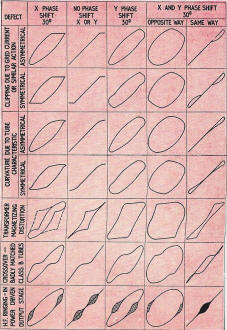
Fig. 7 - Common forms of distortion with different phase shift
combinations.
If sufficient phase shift were introduced in the feed to the X plates to offset
all the phase shift in the amplifier, the trace would be similar to that in the
last column of Fig. 7. Here again the patterns are distinctly different. Probably
the easiest point to detect the difference is that where the trace divides: In the
pattern due to clipping, the curve splits abruptly, but in the pattern due to curvature
it forks apart smoothly.
The next line of patterns illustrates the kind of distortion due to magnetizing
current in a transformer core. For the previous patterns it would be immaterial
which kind of X phase shift were introduced (by itself), because the pattern with
no phase shift has a kind of symmetry demonstrated by the fact that the spot retraces
its path to produce a single line trace. With this kind of distortion, such symmetry
cannot exist, so 30° phase shift produces a different pattern, according to
which way the phase is shifted. One direction is indicated in the figure by the
solid line, and the opposite kind of phase shift, where it follows a different course,
by the dotted line .
Where the phase shift through an amplifier is progressive, as at low frequency,
the dotted line pattern would be the one seen, but where a similar phase shift is
inserted in the deflection to the X plates, the solid line pattern would be produced.
The effect of phase shift after the point of distortion is shown in the "Y shift
30°" column, and combinations of phase shifts in the remaining two columns.
Another kind of distortion that produces patterns somewhat similar to transformer
core distortion in some phases occurs when tubes in class-B operation are badly
matched so that one tube cuts off before the other starts to conduct. A variety
of patterns for this case is shown in the next line of the figure.
The last line illustrates the kind of pattern produced when high-frequency ringing
occurs in the drive transformer of an output stage where positive excursions of
the output tube grids are encountered. The ringing is due to shock excitation of
an ultrasonic resonant frequency in the drive transformer circuit each time grid
current ceases.
A further article will show how the oscilloscope can be used for localizing unexpected
factors in the performance of an amplifier.
Posted October 23
|
















