|
Dec '40/Jan '41 National Radio News
 [Table
of Contents] These articles are scanned and OCRed from old editions of the
National Radio News magazine. Here is a list of the
National Radio News articles I have already posted. All copyrights are hereby acknowledged. |
As mentioned in an earlier
article, National Radio Institute (NRI) was one of the first companies to exploit
the burgeoning field of electronics in the early part of the last century. They
invested heavily in facilities and resources for producing educational material
for both classroom and correspondence courses. Up until sometime in the early 1990s
when throw-away electronics and almost total offshore manufacturing became the rule
rather than the exception, there were always large advertisements in magazines offering
to rescue floundering career seekers with promises of untold opportunities and riches
from servicing radios, televisions, home appliances, and more. That is not
to say the courses were not valuable - they were. Regular newsletters and other
publications were mailed to participants, usually containing good advice on troubleshooting,
circuit theory, component selection, how to handle customers who try to skip out
on paying you, etc. This particular edition of National Radio New discuses current
carrying capabilities of various size wires - a topic that never goes out of style.
The Laboratory Page: Current-Carrying Capacity of Wires
By George J. Rohrich
George J. Rohrich, Engineer in Charge N. R. I. Laboratory
The purpose of this department is to furnish supplemental experiments to students
who have completed their Home Laboratory course, but who wish additional laboratory
experience. You are not required to perform these experiments, but you will gain
increased knowledge by doing so.
Most of the material required will be that received as part of the Laboratory
Course. Any other material necessary can be purchased very reasonably and will constitute
an investment rather than an expense, as it will serve as replacements in service
work or be useful in your shop later.
The Current-Carrying Ability of Resistors
A resistor can be constructed to have a given value of resistance by employing
different sizes of wire. For instance, we can construct a 500 ohm resistance of
very fine wire and it will be necessary to use only a few feet of such wire in order
to obtain 500 ohms.
This particular wire can carry only a given amount of current without becoming
excessively heated.
If we find that the 500 ohm resistor becomes excessively hot, then it will be
necessary to obtain another resistor which is constructed of larger wire. In order
to maintain the same value of resistance, it will be necessary to use a greater
length of the larger sized wire. The same amount of heat will be produced in the
larger wire but its larger surface will radiate heat quickly, keeping it cool.
If we find that the resistor has to carry considerable current, then it may be
necessary to use very large wire.
From the above explanation, we see a resistor has to be constructed so as to
carry a given ·amount of current. Of course. a resistor which is capable of carrying
a large current can also safely carry a smaller current.. The usual practice is
to construct a resistor which can safely handle the maximum current which will be
flowing through it at any time. There is no economy in constructing a larger resistance
when a smaller one will do, unless the smallest allowable size is mechanically fragile
and difficult to handle.
Instead of rating a resistor in its current carrying capacity, it is customary
to rate the resistor as "capable of dissipating a given amount of heat." This rating
is given in watts. This rating in watts is obtained by multiplying the value of
current itself, and finally multiplying this result by the value of resistance.
This is expressed in a formula; Watt = I2R.
For example, let us say that we find a 500 ohm resistance carries 2 amperes.
Multiplying 2 amperes by itself, we obtain 4. Multiplying 4 by 500 ohms we obtain
2000 watts. This is the rating of the resistor and we say that it is capable of
carrying 2 amperes.
The rating in watts can be obtained by a second method. This requires you to
multiply the voltage across the resistor by the current. This is expressed by the
formula: Watts = E x I.
A 500 ohm resistance which has a lower rating in watts is intended to carry a
smaller current. This current carrying capacity can be obtained by dividing the
value in watts by the value of resistance, and then taking the square root of the
result. Thus, a 1/2-watt, 500-ohm resistor is intended to carry currents which are
not greater than 0.031 ampere or only 31 milliamperes.
 You will notice that the relation between
watts, voltage and current is expressed by an equation which is similar to the equation
of Ohm's Law which shows the relation between voltage, current and resistance. Remember
these two equations:
Voltage = current x resistance.
Power = voltage x current.
In order to help you remember them keep in mind these four numbers: 2, 3, 6 and
12 and associate the 2 with current, the 3 with resistance, the 6 with voltage and
the 12 with power.
We know that 6 = 2 x 3.
Therefore voltage = current x resistance.
We also know that 2= 6 ÷ 3.
Therefore current = voltage ÷ resistance.
We know that 3 = 6 ÷ 2.
Therefore, resistance = voltage ÷ current.
We know that 12 = 6 x 2.
Therefore, power = voltage x current.
We know that 12 = 2 x 2 x 3.
Therefore, power = current x current x resistance. This represents the equation
W = I2R.
We know that 12 = (6 x 6) ÷ 3. Thus, power = voltage x voltage, divided
by the resistance. This represents the equation W = E2+R.
We know that 3 = (6 x 6) ÷ 12. Thus, resistance = voltage x voltage divided
by the power. This represents the equation R = E2 ÷ W.
We know that 2 = √ (12 ÷ 3). Thus, current =the square root of the
result which is obtained when the power is divided by the resistance. This is represented
by the equation: I = √ (W ÷ R).
We know that 6 = √ (12 x 3). Therefore, voltage equals the square root
of the result which is obtained when the power is multiplied by the resistance.
This represents the equation E = √ (W x R).
We know that 3 = 12 ÷ (2 x 2). Therefore, resistance equals power divided
by the square of the current. This is represented by the equation: W ÷ I2.
We know that 6 = 12 ÷ 2. Therefore voltage = power ÷ current. The
symbol equation is represented by E=W ÷ I.
We know that 2 = 12 ÷ 6. Therefore, current = power ÷ voltage.
The symbol equation is I = W ÷ E.
With these twelve equations you can find the value of anyone of the four quantities,
provided you know the value of two other quantities. You can see how easy it will
be for you to work out anyone of the twelve if you will only remember the two equations
to which I called your attention above.
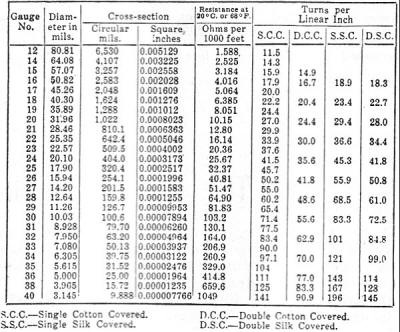
The current carrying-capacity of a wire used in a circuit or electrical instrument
is dependent on the size of the wire. It is customary to allow 1000 circular mills
of cross-sectional area for each ampere where copper wire is exposed to good ventilation.
Where the wire is used so that air cannot reach it freely for carrying off the generated
heat, it is customary to allow 1500 circular mills for each ampere.
The cross-section area of various wires is shown in the accompanying table.
For instance a No. 30 wire has a cross section area of approximately 100 circular
mills. This wire is used for carrying 0.1 ampere where the wire is exposed and it
is used to carry a maximum of 0.066 ampere where the wire is confined to close places.
A No. 30 wire will burn out when a current of 10 amperes flows through the wire.
A No. 38 wire has a cross sectional area of 15.72 circular mills and it is rated
to carry 16 milliamperes and 10 ma. under the two conditions. This wire will burn
out with 2.5 amperes.
The milliammeter furnished with the experimental parts uses No. 38 wire.
For ordinary purposes it may be remembered that a wire will not burn out until
a current of 50 times to 150 times the allowable current-carrying capacity of the
wire flows through the wire.
Posted December 27, 2021
(updated from original post on 5/28/2014)
|
