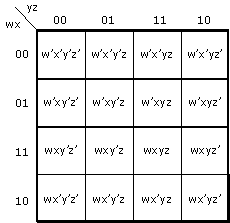•−•  ••−•    −•−•  •−  ••−•  • RF Cafe Morse Code >Hear It<
Job Board
About RF Cafe©
RF Cafe E-Mail

Karnaugh Maps / Tables

The Karnaugh map, also known as a Veitch diagram (KV-map or K-map for short), is a tool to facilitate the simplification of Boolean algebra integrated circuit expressions. The Karnaugh map reduces the need for extensive calculations by taking advantage of human pattern-recognition and permitting the rapid identification and elimination of potential race hazards.

The Karnaugh map was invented in 1952 by Edward W. Veitch. It was further developed in 1953 by Maurice Karnaugh, a physicist at Bell Labs, to help simplify digital electronic circuits.

In a Karnaugh map the boolean variables are transferred (generally from a truth table) and ordered according to the principles of Gray code in which only one variable changes in between squares. Once the table is generated and the output possibilities are transcribed, the data is arranged into the largest even group possible and the minterm is generated through the axiom laws of boolean algebra. - Wikipedia

Karnaugh Map (also known as the Veitch Diagram) reduction was developed as a graphic method of minimizing Boolean function. The 4-variable Karnaugh Map reduction shown here applies to any size map.

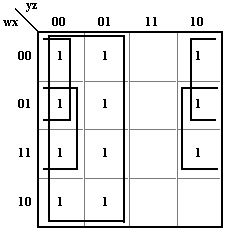
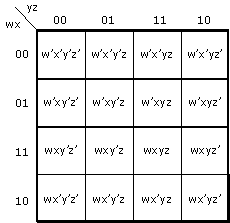
Example 4-Variable Map Problem      F(w,x,y,z) = ∑(0,1,2,4,5,6,8,9,12,13,14)                = y+w·z+x·z Minterms must be boxed in the smallest number of groups which results in all minterms being enclosed.	Generic 4-Variable Map     Note that w,x,y,z terms (and their compliments) are arranged in positions corresponding to the axis labels. One unique minterm exists in each square.
Generic 2-Variable Map	Generic 3-Variable Map

A Disruptive Web Presence™ Custom Search Over 10,000 pages indexed! (none duped or pirated)	Read About RF Cafe Webmaster: Kirt Blattenberger     KB3UON	RF Cafe Software RF Cascade Workbook RF system analysis including frequency conversion & filters RF & EE Symbols Word RF Stencils for Visio
	Product & Service Directory Personally Selected Manufacturers
	RF Cafe T-Shirts & Mugs
	RF Cafe Software Calculator Workbook RF Workbench Smith Chart™ for Visio Smith Chart™ for Excel