Electronics World articles Popular Electronics articles QST articles Radio & TV News articles Radio-Craft articles Radio-Electronics articles Short Wave Craft articles Wireless World articles Google Search of RF Cafe website Sitemap Electronics Equations Mathematics Equations Equations physics Manufacturers & distributors Engineer Jobs LinkedIn Crosswords Engineering Humor Kirt's Cogitations Engineering Event Calendar RF Engineering Quizzes USAF radar shop Notable Quotes App Notes Calculators Education Engineering Magazines Engineering magazine articles Engineering software Engineering smorgasbord RF Cafe Archives RF Cascade Workbook 2018 RF Stencils for Visio RF & EE Shapes for Word Advertising RF Cafe Homepage Sudoku puzzles Thank you for visiting RF Cafe!
Exodus Advanced Communications

Transmission Line Equations

Transmission lines take on many forms in order to accommodate particular applications. All rely on the same basic components - two or more conductors separated by a dielectric (insulator). The physical configuration and properties of all the components determines the characteristic impedance, distortion, transmission speed, and loss.

See a discussion on transmission lines and coaxial connectors.

The following formulas are presented in a compact text format that can be copied and pasted into a spreadsheet or other application.

For the following equations, ε is the dielectric constant (ε = 1 for air)

Two Conductors in Parallel (Unbalanced)
Above Ground Plane

For D << d, h

Z0= (69/ε½) log10{(4h/d)[1+(2h/D)2]-½}

Parallel conductors above a ground plane - RF Cafe
 Single Conductor Above Ground Plane
 
For d << h

Z0= (138/ε½) log10(4h/d)

Single conductor above a ground plane - RF Cafe
Two Conductors in Parallel (Balanced)
Above Ground Plane

For D << d, h1, h2

Z0= (276/ε½) log10{(2D/d)[1+(D/2h)2]-½}

Parallel conductors above a ground plane - RF Cafe
 Two Conductors in Parallel (Balanced)
Different Heights Above Ground Plane

For D << d, h1, h2

Z0= (276/ε½)log10{(2D/d)[1+(D2/4h1h2)]-½}

Parallel conductors different heights above a ground plane - RF Cafe
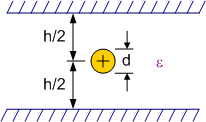
Single Conductor Between
Parallel Ground Planes

For d/h << 0.75

Z0= (138/ε½) log10(4h/πd)

Single conductor between parallel ground planes - RF Cafe

 Two Conductors in Parallel (Balanced)
Between Parallel Ground Planes

For d << D, h

Z0= (276/ε½) log10{[4h tanh(πD/2h)]/πd}

Two conductors between parallel ground planes - RF Cafe
Balanced Conductors Between
Parallel Ground Planes

For d << h

Z0= (276/ε½) log10(2h/πd)

Balanced conductors between parallel ground planes - RF Cafe

 Two Conductors in Parallel (Balanced)
of Unequal Diameters




Z0= (60/ε½) cosh-1 (N)

N = ½[(4D2/d1d2) - (d1/d2) - (d2/d1)]

Parallel conductors - unequal diameters - RF Cafe
Balanced 4-Wire Array

For d << D1, D2

Z0= (138/ε½) log10{(2D2/d)[1+(D2/D1)2]-½}

Balanced 4-wire array - RF Cafe
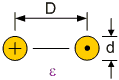
 Two Conductors
in Open Air


Z0= 276 log10(2D/d)

Two conductors in open air - RF Cafe
5-Wire Array

For d << D

Z0= (173/ε½) log10(D/0.933d)

5-wire array - RF Cafe
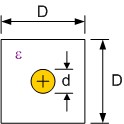
 Single Conductor in
Square Conductive Enclosure

For d << D

Z0≈ [138 log10(ρ) +6.48-2.34A-0.48B-0.12C]/ε½

A = (1+0.405ρ-4)/(1-0.405ρ-4)

B = (1+0.163ρ-8)/(1-0.163ρ-8)

C = (1+0.067ρ-12)/(1-0.067ρ-12)

ρ= D/d

Single conductor in square conducting enclosure - RF Cafe
Air Coaxial Cable with
Dielectric Supporting Wedge

For d << D

Z0≈ [138 log10(D/d)]/[1+(ε-1)(θ/360)]½)

ε = wedge dielectric constant

θ= wedge angle in degrees

Air coaxial cable with dielectric supporting wedge - RF Cafe
 Two Conductors Inside Shield
(sheath return)

For d << D, h

Z0= (69/ε½) log10[(ν/2σ2)(1-σ4)]

ν = h/d       σ = h/D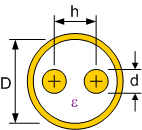

Twin conductors inside shield - RF Cafe
Balanced Shielded Line

For D>>d, h>>d

Z0= (276/ε½) log10{2ν[(1-σ2)/(1+σ2)]}

ν = h/d       σ = h/D

Balanced shielded line equation - RF Cafe
  
Two Conductors in Parallel (Unbalanced)
Inside Rectangular Enclosure

For d << D, h, w

                          ∞
Z0= (276/ε½) {log10[(4h tanh(πD/2h)/πd)- ∑ log10[(1+μm2)/(1-νm2)]}
                            m=1

μm=sinh(πD/2h)/cosh(mπw/2h)

νm=sinh(πD/2h)/sinh(mπw/2h)

Balanced 2-conductor line inside rectangular enclosure - RF Cafe

 

 

Equations appear in "Reference Data for Engineers," Sams Publishing 1993
Windfreak Technologies withwave microwave devices - RF Cafe
Res-Net Microwave - RF Cafe LadyBug Technologies LB479A RF Power Sensor - RF Cafe
About RF Cafe
Kirt Blattenberger - RF Cafe Webmaster
Copyright: 1996 - 2024
Webmaster:
    Kirt Blattenberger,
    BSEE - KB3UON

RF Cafe began life in 1996 as "RF Tools" in an AOL screen name web space totaling 2 MB. Its primary purpose was to provide me with ready access to commonly needed formulas and reference material while performing my work as an RF system and circuit design engineer. The World Wide Web (Internet) was largely an unknown entity at the time and bandwidth was a scarce commodity. Dial-up modems blazed along at 14.4 kbps while typing up your telephone line, and a nice lady's voice announced "You've Got Mail" when a new message arrived...

All trademarks, copyrights, patents, and other rights of ownership to images and text used on the RF Cafe website are hereby acknowledged.

My Hobby Website:  AirplanesAndRockets.com

spacer

Please Support RF Cafe by purchasing my  ridiculously low−priced products, all of which I created.

These Are Available for Free