|
November 1969 Electronics World
 Table of Contents
Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
Electronics World, published May 1959
- December 1971. All copyrights hereby acknowledged.
|
I have always found it
annoying when an author uses a symbol or subscript in an article without explaining
or somehow making obvious what it is. In this "Resistivity: Some Definitions" piece
from a 1969 issue of Electronics World magazine, the author's stated purpose
is to define terms related to resistivity, which he does well, but there are a couple
instances where subscripts for resistivity, rho (ρ),
are left for the reader to figure out. ρsp,
ρs, and ρv
have been replaced with ρspecific,
ρsheet, and ρvolume
, respectively, where needed. Sure, a careful reading of the surrounding content
clarified the intent, but you are not supposed to work that hard. Otherwise, this
is a great primer on the meaning of resistivity, how it is measured, and how it
is used to calculate the resistance of a device. Caution is advised in noting
and staying consistent with stated resistivity units when performing calculations.
Resistivity: Some Definitions
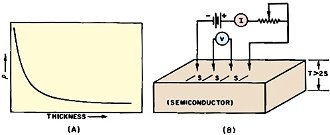
Fig. 1 - (A) In thin films, resistivity varies logarithmically.
Four-point probe (B) is used to measure crystal resistivity.
By Joseph Tusinski
Chief Technical Instructor, Old Dominion College
Often when defining technical terms or using them in an equation, many technical
men confuse them and unknowingly employ wrong expression.
Engineers as well as technicians some time have difficulty defining resistivity.
Resistivity and resistance are both related to the ability of a substance to impede
the drift of electronic charges. However, in specifically defining one or the other,
dimensions used in formulating each term are either disregarded or not even considered.
Resistance has dimensions of mass, length, time, and charge. Hence it is defined
in terms of volts per ampere. The unit of resistance is the ohm and its symbol is
capital omega (Ω). For example, when 100 Ω is expressed, what is implied
is 100 volts per ampere. Resistivity, on the other hand, is given in terms of resistance
per volume and its symbol is rho (ρ). Thus a problem
normally involves resistivity when it appears in a formula and the wrong dimensions
are used, or it would be more appropriate to say not used. Care should be exercised
in using tables of resistivities because, in many cases, identical substances may
have different numerical values of resistivity.
Resistivity appears subscripted in a number of ways. Some are:
ρspecific,
ρvolume,
ρrelative,
ρsurface,
ρsquare,
ρbulk,
ρsheet,
ρlattice,
and ρimperfection
Lattice and imperfection resistivity deal with lattice vibrations and imperfections
of a crystallographic structure. Hence technicians familiar with how semiconductors
and thin-films are made will encounter these terms as well as sheet resistivity.
Sheet resistivity may be encountered in a number of fields such as thin-film technology
or microwaves.
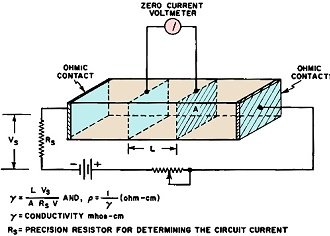
Fig. 2 - To measure bulk resistivity, current must be forced
through the material and the resulting voltage drop measured.
It should be mentioned here that all discussion about resistivity in this article
refers to a homogeneous material. A heterogeneous material may be physically attainable
or it may be obtained by virtue of frequency effects, such as skin-effect (see the
author's article "What is Skin Effect?," June 1963 issue of this magazine).
Fig. 1A shows that for very thin films, resistivity varies logarithmically and
that for thicker materials, the resistivity curve flattens out. A four-point probe
method (Fig. 1B) is used to measure sheet resistivity of semiconductor crystals.
If the thickness of the crystal is more than twice the probe spacing, the resistivity
of the material can be expressed by the equation:
ρsheet
= (2π Vs)/l
where s = probe spacing, V = voltage measured with a zero-current voltmeter, l =
constant current source, and 2π = 6.2832.
Bulk resistivity,
ρ∞,
is another term used to describe the resistivity or the impurity concentration of
a semiconductor. Ordinarily, when the resistivity of a material is measured, a known
current is forced through the material and the resulting voltage drop is measured.
Thus by Ohm's Law (R = E/I) the resistance is determined and related to resistivity
in ohms/cm3. Very often the term is shortened to ohm-cm, the cube being
implied. However, in bulk resistivity measurements, the resistance of the ohmic
contacts must not be included in calculations. Thus a method somewhat similar to
the four-point probe method is used (Fig. 2).
Square resistivity is perhaps the most misunderstood of all. Technicians usually
ask, "Square what?" or they assume that a square centimeter is implied. The implication
of square resistivity is that the length of the sample is equal to the width, i.e.,
is square. Resistivities are given in ohms/square. For example, assume a sample
of material having a resistivity of R ohms/square. Thus if four of the basic units
are combined, the length doubles, hence the resistance doubles (2R); however, the
width also doubles, which is the same as paralleling two resistors having values
of 2R each. The total resistance of the combination is: 2R x 2R / (2R + 2R) = R.
A simile can be derived by increasing the length three times and the width three
times, i.e., square. The total resistance is: 1/(1/3R + 1/3R + 1/3R) = R.
For example, suppose it is desired to achieve a resistance of 15 kΩ
with a material having a resistivity of 300Ω/square. Let us assume that the resistor
must have a minimum width of 20 mils: determine the length of the resistor. From
R = ρsquare
(L/W), L = WR/ρsquare
then L = (0.02 x 15,000)/300, or 1 inch. This equation states that to determine
the resistance of a specimen, the square resistivity is multiplied by the ratio
of the length to the width.
The use of specific, volume, and relative resistivities is normally relegated
to metals. These are perhaps the most popular tables of resistivity available, and
yet erroneous conclusions arise from their use.
In electronics, copper wire has been the most popular material used to interconnect
components. For this reason, many tables list the various characteristics of copper.
However, the characteristics of copper may be altered by various means (alloying
or annealing). Therefore a certain type of copper is used as a standard in evaluating
the conductivities of materials (γ = 1/ρ).
The standard, which represents 100 percent conductance, is annealed copper at
a temperature of 20° C. The resistance of a one-meter-long section having a uniform
cross-section of 1 mm is equal to 0.01724 ohm. Other methods were tried dealing
with the weight of copper; however these were not too fruitful, and the measurement
of length and area became the popular way to standardize.
The conductivity of aluminum may vary by as much as 35 percent depending upon
its composition. Pure aluminum (99.97 percent) has a conductivity of 64.6 percent
of standard copper. Thus if standard copper is considered to be unity, aluminum
has a relative resistivity of 1/0.646 = 1.54 or a specific resistance 1.54 times
that of standard copper. Thus values derived from a table consisting of relative
resistivities must be multiplied by the resistivity of copper to determine their
actual or specific resistance.
Tables relating the resistivity of a round copper wire were quickly formulated
so that most of the arithmetic could be simplified. From these, a table of specific
resistivities evolved. The popular dimensions chosen were the one -nail diameter
and one-foot length (the mil-inch was adopted in England). Thus they yield the specific
resistance of a material one-mil by one-foot, normally classified as Ω/mil-foot.
For example, annealed copper would have a specific resistivity of 10.36Ω/mil-foot.
Volume resistivities relate the resistance of a cubic structure. They are specified
as follows: 1. Ω/cm-cube (preferred), 2. Ω-cm, and 3. microhm-centimeters.
All three designations refer to a cubic specimen having square faces of one centimeter.
The resistance is to be measured between flat plates making contact with opposing
faces. Standard copper has a volume resistivity of 1.7241 X 10-6Ω/cm-cube
or 1.7241 microhm-cm. When
ρspecific,
and ρvolume
of copper are compared (1.7241 microhm-cm compared to 10.36Ω/mil-foot) and dimensions
disregarded, serious mathematical errors result. A simple example will help to illustrate
this point. The resistance of any uniform homogeneous material is given as R =
ρL/A (ohms).
It is obvious that if
ρ = 1.64,
or ρ =2.83
x 10-6, or
ρ = 16.9
is used in the equation, different results would be obtained. However, all of these
resistivities (relative, volume, and specific) are given for the same material.
Thus in order for the calculated resistance to be meaningful, the units of L and
A must be converted to correspond to the method used in determining the resistivity
of the material.
Another factor should be mentioned about determining resistivities of insulators.
For example, the surface resistivity of an insulator is measured from the opposite
edges of a square specimen. The bulk resistance of the body, which is parallel to
the surface, must be many times greater than the surface resistance. The volume
resistivity of an insulator must be determined using sophisticated guarding procedures,
so that surface charges will not mask uniform conduction through the sample. All
of the resistivities discussed are by no means all of the various forms of resistivity
that the technician or engineer will encounter. The intent is to bring about a respect
for a numerical value of resistivity and to be concise in specifying the dimensions,
method used, or theory involved in determining a value of rho.
|









