|
October 1960 Electronics World
 Table of Contents Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
Electronics World, published May 1959
- December 1971. All copyrights hereby acknowledged.
|
Capacitors come in a huge variety
of package configurations, chemical makeups, physical constructions and sizes, capacitance
values, and voltage and power handling abilities. Each has its own strengths and
weaknesses for a particular application. When capacitors are functioning properly,
life is great, but when one decides to fail either completely or partially, troubleshooting
the cause can be a real challenge. The best kind of electrical component failure
from a troubleshooting perspective is one where the component releases its life-giving
internal smoke and in the process leaving a clearly visible clue like a cracked
case or a nice black mark when none should be. Otherwise, the job can get interesting.
Being proficient at schematic reading and tracing waveforms through circuits is
a real benefit, but that option is not always available, as in the case of undocumented
equipment. In that situation, experience and intuition might be your only hope.
This article gives some pointers that can put another method or two in your collective
bag of tricks.
Wayward Capacitor Woes
By Allan F. Kinckiner

Fig. 1 - Sensitive capacitor leakage measurement.
Look out for "perfectly good" capacitors that pass all tests but produce strange
and confusing faults.
Every technician is confronted at one time or another by tubes that pass every
test on the very best tube checkers but simply will not work properly in certain
circuits, although a substituted tube will. After a number of such experiences,
the technician adopts the following credo: If a tube is suspected, don't rely on
a check-substitute.
Another electronic component that often presents the same baffling condition
of causing circuit malfunction while passing every test is our friend the capacitor.
A look at what tests these components are subjected to in the better capacitor analyzers
reveals the following: capacitance measurement (generally quite accurate) and leakage
(the amount of direct current the component will pass). In the latter check, a substantial
d.c. voltage is fed into one terminal of the component, which is in series with
a voltage-reading meter. Some analyzers use eye tubes or neon bulbs in place of
the meter.
A more efficient leakage test is to use a source of several hundred volts (depending
on the component's rating) applied to one terminal of the capacitor, which is series-connected
to a v.t.v.m., as in Fig. 1. Leakage resistance may then be determined from the
following relationship: Rc/Rm = Ec/Em;
where Rc is the leakage resistance of the capacitor, Rm the
input d.c. resistance of the v.t.v.m. (usually 11 megohms), Ec is the
voltage across the capacitor, and Em is the voltage read on the meter.
In the example shown, the meter reading (Em.) is .1 volt, which leaves
299.9 volts as Ec. Solving for Rc, we we have a leakage resistance
of almost 33,000 megohms. The leakage current, determined by Ohm's Law, would come
to less than a hundredth of a microampere. Insignificant as these leakage figures
seem, there are circuits in which capacitor replacement would be warranted.
The advantages of checking leakage in this way are twofold. First, the sensitivity
is greater than in the test provided by most analyzers. In the second place, leakage
is more easily read. A man could get eyestrain trying to judge the opening or closing
of an eye tube or the lighting of a neon lamp. However, just as the tube checker
should be neither condemned nor scrapped because it doesn't bat one thousand, the
capacitor analyzer should not be demoted for its less-than-perfect score on the
leakage test.

Fig. 2. - Preamp in which noise was generated by a "good" ceramic
capacitor.
It is true that the substitution of a suspected capacitor is not so easily accomplished
as that of a tube. Yet this will often be the quickest path to a repair. However,
the substitution should only be considered after thorough circuit testing has left
the capacitor as the prime suspect, although on circumstantial evidence. The capacitor
fault may be so elusive that it will not always be possible to, determine exactly
what defect has occurred, although malfunction disappears when a substitution is
made. Following are several accounts of skirmishes with capacitors, to prove the
points made.
Before going into the case histories, we should like to point out another parallel
between tubes and capacitors. The baffling defects are most likely to occur in more
critical electronic circuits, such as low-level amplifiers, discriminating or limiting
networks (such as the sync stages), sine and other waveform generators (such as
TV deflection generators), and in other pulse-handling or pulse-forming circuits.
The Sizzling Ceramic
A V-M model 711 tape recorder came in for service with the complaint of being
noisy. Inspection revealed that, with no tape threaded on and with the "play" button
depressed, a constant sizzling noise could be heard. The latter could be attenuated
by adjusting the volume control, indicating that the trouble was in a preceding
stage (or perhaps in a later stage, but was being detected by the sensitive preamplifier).
A scope check quickly eliminated the alternate possibility in this instance.
The preamplifier consisted of a 12A-X7 with the triodes in cascade (see Fig.
2.) Further troubleshooting revealed that grounding the second grid killed the noise,
but grounding the first grid had no effect. The sizzling noise sounded precisely
like a noisy resistor, so the resistors were substituted after resistance and voltage
checks in the order numbered, but without any result.
Capacitor Cx was disconnected at the second grid and checked with
an analyzer, which passed it as being faultless. Cx was also checked
as per the technique discussed in connection with Fig, 1; not the slightest leakage
was indicated. Since every other component in the circuit had been substituted,
Cx was now temporarily replaced with a tacked-in unit, and dawg-gone
if that didn't cure the trouble.
This capacitor, a black .01-μf. disc ceramic, subjected to all types of further
testing on our brand X capacitor analyzer, was also checked on a fellow service
technician's brand Y analyzer. It passed without even the slightest indication of
fault.
Shifting Height


Fig. 3. - Low (A, top) and proper (B, bottom) sinewave height
in Synchroguide waveform.
A TV set came in with the complaint that raster height was insufficient, with
the compression occurring on the bottom. The condition occurred only after the receiver
had been operating an hour or more, and would get progressively worse. After the
saw-tooth forming capacitor in the vertical circuit had been replaced, the bottom
of the raster was easily stretched out to fill the bottom of the CRT screen with
normal linearity. Furthermore, the raster remained constant in vertical size, without
needing later readjustment.
The capacitors that produce the not uncommon defect noted here are generally
of the waxed paper type. Their capacitance may tend to increase as their temperature
goes up. While a capacitor analyzer is quite capable of indicating an increase in
capacitance, it can do so only if the suspected component is heated to the temperature
at which it works in the receiver. Thus, tacking in a replacement is the quickest
way to make a satisfactory check.
Sneaky Plastics
The horizontal Synchroguide circuit is one of those where capacitors can really
raise havoc. For example:
The fellow service technician previously referred to as the owner of the brand
Y analyzer sought help on a tough dog. It was an RCA KCS34B that would not hold
horizontal sync for more than twenty minutes. In answer to questioning, he insisted
that he had disconnected and tested all the capacitors in the circuit and that all
read up to par on his analyzer. Knowing him to be a thorough technician who normally
makes the necessary resistance, voltage, and scope checks when he has trouble, we
advised him to tack-solder capacitor substitutions.
About one hour later he phoned with the information that, "after replacing the
.002 μf. that feeds the sync and sampling pulses to the grid of the a.f.c. triode
(C1 in Fig. 5), the trouble was corrected." While he was happy that he
had repaired the set, he was also extremely unhappy because his expensive analyzer
would not indicate anything wrong with the replaced unit. The .002-μf. unit was
one of those black, plastic-encased capacitors.
In line with this experience involving Synchroguides, one set, an RCA KCS84F,
operated relatively normally except that the horizontal sync was critical. It was
noticed during troubleshooting that the frequency slug of the oscillator transformer
adjusted at an extremely withdrawn position. Component and voltage-checking tests
revealed nothing, so the various frequency-determining capacitors were temporarily
replaced. When C2 in Fig. 5 was replaced, not only did the frequency
slug adjust to a more orthodox position, but the horizontal saw-tooth waveform increased
from 130 to over 160 volts, peak-to-peak, as a scope check showed. As a result other
improvements occurred; the width increased, as did the high voltage, with improved
focusing.
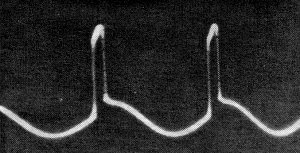

Fig. 4. - Low (A. top) and proper (B, bottom) sine-wave height
in multivibrator waveform.
C2 was also a black, plastic-encased tubular; it too passed all tests,
including leakage, and its measured capacitance was within ten percent of nominal
value although it was only rated at twenty percent. We are not exactly sure what
the elusive fault is that occurs in units of this type, but suspect that the pulsed
nature of the voltage to which they are subjected causes them to react erratically
in a way that does not show up on static tests.
Watch That "Q"
On to case 4: The stabilizing network in the Synchroguide circuit is a tank that
generates a sine wave at approximately the horizontal sync frequency. This plays
an important role in maintaining synchronization in the presence of random pulses
that might otherwise trigger the oscillator falsely. The network consists of an
adjustable coil shunted by a capacitor.
In Fig. 5, this network consists of C3 shunted by Lp, with
the latter being known as the phasing coil. Stabilizing efficiency is affected by
the over-all "Q" of the tank, which is affected by the "Q" of C3 specifically.
This factor may decrease over a period of time, reducing sine-wave amplitude.
Analyzers will not indicate this lowered "Q" factor, but it can be determined
with the scope. The waveform of Fig. 3A was noted at point C of a Synchroguide used
in a '53 Philco. Note that, while the phasing coil is adjusted properly, the sine-wave
amplitude is about 15 percent of the composite waveform's total amplitude. The waveform
of Fig. 3B was noted at the same point after C3 was changed. Note now
that the sine-wave amplitude is nearly 25 percent of the composite amplitude. This
change improved horizontal synchronization in this particular receiver considerably.
In multivibrator-type horizontal oscillators, the stabilizing tank again consists
of an adjustable coil (usually called the ringing coil) shunted by a capacitor.
The coil's action parallels that of the phasing coil in that it generates a sine
wave each time the oscillator plate switches on to draw current. The tank is invariably
in series with a resistor in the plate lead of the multi vibrator's controlling
(first) triode. The stabilizing efficiency of this network is similar to that of
the one in Fig. 5, and similar problems may occur.

Fig. 5. - Synchroguide oscillator with sinewave generating tank
(Lp and C3).
The relative "Q" factor of the tank in these circuits can also be determined
with the scope. Fig. 4A was taken at the plate of the first triode of a horizontal
multivibrator in a Motorola. Note that the amplitude of the sine wave is about 30
percent of the composite waveform's amplitude. Fig. 4B was taken at the same point
after the tank's capacitor was changed. Now the sine wave scopes better than 50
percent of the total waveform height. The replacement cleared up a complaint that
setting of the horizontal hold control was too critical.
The ratios given here for sine-wave amplitude to overall waveform height are
those most often used in original design for Synchroguide and multivibrator circuits,
although they are not universal. In general, where marginal horizontal-hold is the
problem and no other defects exist, approximating these ratios will produce enough
improvement to satisfy an unhappy customer.
The change in the capacitor, over a period of time, that produces this reduction
in sine-wave amplitude sheds light on the tendency of older sets to develop more
critical-sync.
Capacitor Or Rectifier?
A Philco TV about nine years old was benched for drifting vertical lock. The
hold control had to be readjusted every ten minutes until it reached the end of
its rotation, after which rolling could not be stopped. Trouble of this nature is
due to gradual changes in such frequency-determining oscillator components as resistors
(including the control), the blocking oscillator transformer, and, of course, the
coupling and timing capacitors. In this case, replacing a capacitor corrected the
trouble.
Suspected of leakage, the capacitor had been checked on an analyzer but no leakage
had been found. When it was checked again after the replacement had worked, there
was considerable leakage. Further checking showed that, when the capacitor was connected
to the tester in one way, there was still no leakage. However, when the capacitor
leads were reversed, leakage was clearly indicated! Evidently the component had
begun to act like a semiconductor, passing current in one direction only. It was
weird but it happened. The unit was a .01-μf. capacitor encased in plastic.
An Eccentric Electrolytic

Fig. 6. - The pointer indicates stain on capacitor case from
electrolyte leakage.
The villain in case 6, unlike the smaller units involved with the other histories
noted so far, was the big brother of the capacitor family, an electrolytic. A Sylvania
TV (Model 540) came in with the complaint that it was erratically blowing a 2.5-ampere
fuse. One fuse might last several days; but the next might only survive for one
hour.
In a bench check, line current was metered at about 1.5 amperes. Receiver operation
was entirely normal, with good picture and sound. Instrument checks revealed no
unusual conditions. However a visual check showed a suspicious chemical staining
at the metal band used to mount a 150-μf., 200-volt electrolytic filter to the
chassis. Unfastening the metal band by removing the self-tapping screw that held
it to the chassis caused the line current to fall to about 1 ampere.
Fig. 6 shows the staining on the cardboard case of this unit, with the metal
band removed to render the symptom more visible. This type of electrolyte leak-through
on cardboard-cased units was more common in prewar radios, where it often led to
puzzling hum problems. Service technicians can be grateful that the difficulty doesn't
arise so often these days, but they should keep in mind the fact that it can occur.
One end of this capacitor was connected directly to one side of the a.c. line in
a voltage doubler using two selenium rectifiers, which is why the leakage blew fuses.
However, an analyzer would not have indicated abnormal leakage.
Thus we close the file on wayward capacitors. In each of the cases described
here, the defects were of the kind that would escape detection with capacitor analyzers
or other direct instrument checks. In each, secondary evidence was the only indication
that the capacitor might be at fault. In closing, a few words of commendation might
be said for that old standby, the oscilloscope. As in several instances recounted
here, its role in revealing the secondary conditions that lead to apprehension of
guilty capacitors with off-beat defects is important.
Posted August 26, 2019
(updated from original post on 3/25/2014)
|



































