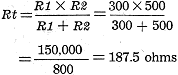How to Use Ohm's Law, February 1956 Popular Electronics

Fortunately, there is a constant flow of people newly interested in electronics who are seeking information on basic principles. Some will find an article like this one on Ohm's law fundamentals and decide maybe being just a user of electronics is good enough. Others will, as did you and I, read this kind of material and be amazed at how ultimately predictable electrical circuit parameters are. If he or she continues and launches into a career in electronics or electrical engineering, it won't be long before he or she will, as do you and I now, look back at how simple things were at the beginning of the journey ;-) This 1956 Popular Electronics magazine article was written half a century ago, but to a word everything contained herein is as valid today as it was then.

Familiarity with this valuable tool will improve your ability to understand electronic circuits

Most electronic experimenters steer clear of anything that smacks of theory. And with good reason, for if one gets a kick out of working with his hands and building gadgets that do things, pushing a pencil can be mighty boring. But there's one bit of theory that's both easy to learn and easy to use. Best of ail, once learned, it will provide the experimenter with a powerful mental tool that will help him to undertake more difficult and more interesting projects, and may even help him to save money when buying electronic parts ... Ohm's law.

With a knowledge of Ohm's law, the experimenter can do such things as determine what size cathode resistor to employ in an audio amplifier, how large a dropping resistor to install in series vacuum-tube heater strings, and what size multiplier resistor to use when converting a milliammeter to a voltmeter. In many cases, he may be able to combine two resistors that he has in his junk box to use in place of one resistor that he would have to buy, thus saving money on parts purchases.

Ohm's law is not a man-made law like the laws against speeding and robbery but, rather, a statement of natural or scientific law. It is a statement of the relationship between electrical pressure (voltage), resistance to current flow (ohms), and actual current flow (amperes) in a closed electrical circuit. It is named after George Simon Ohm who, in the 1820's, formulated this relationship. The familiar unit of electrical resistance, the ohm, is named after the same scientist.

Ohm's law itself may be expressed in many forms, both as fact statements, and as mathematical formulas. One fact statement is as follows: the current flow (amperage) in an electrical circuit is directly proportional to the total electromotive force (electrical pressure, or voltage) in the circuit and inversely proportional to the total resistance of the circuit.

In actual practice, this fact statement of Ohm's law, as interesting as it may be, is not used nearly as much as the mathematical relationships, or formulas, which are derived from the law. These formulas are given in Fig. 1 (A) in their three basic forms. The small design at the top provides a convenient way for the beginner to remember the relationships. In using these formulas, the numerical values in the basic units of resistance (ohms), voltage (volts), and current (amperes) in every case are substituted for the symbols R, E, and I.

Equipment for testing the circuit of Fig. 3(B). The same equipment may be used for checking all the circuits which are discussed in the text.

To use any of these forms of Ohm's law, it is only necessary to determine two of the values in the circuit, then to substitute them in the proper formula to calculate the third value.

For example, in the basic experimental setup shown in Fig. 1 (B), the electromotive force or voltage E may be determined by a voltmeter, current flow I by an ammeter, and the resistance R may then be calculated by using the third form of Ohm's law, as shown in Fig. 1 (A). But enough of general theory; let's take up some down-to-earth practical examples.

Series Resistor: In transformerless circuits, tube heaters are frequently connected in series across a source of fairly high voltage. This may be done if each heater requires the same current for operation and if the total voltage drop is equal to the source voltage. Where the total voltage required is less than source voltage, a series dropping resistor is connected in the circuit to provide additional voltage drop and thus to limit current flow.

A typical circuit arrangement is shown in Fig. 2 (A). What size resistor should be chosen for R? Let's use Ohm's law and see.

Using round figures, the total voltage drop 4n the tube circuit proper is 35 volts (35W4) plus 50 volts (50B5) plus 12 volts (12AT7), or a total of 97 volts. This can be determined by simple addition. Since the source voltage is 117 volts, it will be necessary to drop 117-97 or 20 volts across the

Resistance. Current? Check the tube manual! For these tubes, heater current is 0.15 amperes. Now, let's substitute these values in form three of Ohm's law, as given in Fig. 1 (A). Resistance (R) = desired voltage drop (20) /current (0.15), or:

But now a problem presents itself. If an experimenter went into a radio parts store and asked for a 133.33-ohm resistor, the clerk would be mighty surprised. In most cases, however, exact circuit values are not too critical, so one should simply ask for the nearest standard value resistor or, in this case, a 150-ohm unit.

Cathode Resistor: A common problem encountered in designing and building audio amplifiers is shown in Fig. 2 (B). What size cathode resistor is needed to bias this power output stage properly? As in the case of the series heater resistor, first consult the tube manual. Let's assume that a type 50C5 tube is being used, with B+ around 110 volts.

Referring to the tube manual, it will be seen that suggested bias voltage is -7.5 volts for this plate voltage, and that, under these conditions, the plate current will be 49 milliamperes, the screen grid current 4 milliamperes. The cathode current is the total of the plate and screen currents, or 49 plus 4 = 53 ma.

Having the voltage (7.5 volts) and the current value (53 ma.), the resistance can be calculated using Ohm's law.

Fig. 1 - (A) Three basic forms of Ohm's law. (B) Experimental circuit for Ohm's law.

Wait a minute! When using Ohm's law, the current must be in amperes if the values are to be determined in volts and ohms. Remembering that 1 milliampere equals 0.001 ampere, simply take the value in milliamperes and move the decimal point three places to the left to convert the value to amperes. Thus, 53 ma. = 0.053 amperes. Now, substituting this value in the formula:

As a 141.5-ohm resistor cannot be purchased, one would then ask the clerk for a 150-ohm unit.

Meter Multiplier: A milliammeter or microammeter may be used as a voltmeter if it is provided with a series resistor to limit current flow. The basic circuit arrangement is shown in Fig. 2 (C). What size multiplier resistor should be used in the circuit? This should be a cinch now that Ohm's law has been learned.

To measure a maximum of 100 volts, a full-scale (1-ma.) reading on the meter should indicate that 100 volts is applied across the entire circuit. Thus, both the voltage (100) and the current (1 ma. or 0.001 ampere) are known. Therefore:

But this is the total resistance needed in the circuit. Since the meter already has a resistance of 50 ohms, the multiplier resistor (R) should have a value of 99,950 ohms. Where maximum accuracy is desired, a special effort should be made to obtain a precision multiplier resistor having the exact value needed. However, for practical purposes, a 100,000-ohm resistor could be used in this circuit.

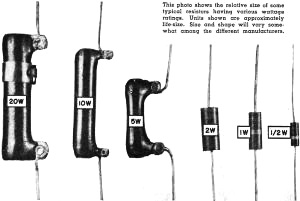
This photo shows the relative size of some typical resistors having various wattage ratings. Units shown are approximately life-size. Size and shape will vary somewhat among the different manufacturers.

Suppose that a resistor is needed of a value that cannot be bought ... or, suppose there are a lot of resistors on hand, but not of the value desired. Is there some way that two or more resistors can be combined to obtain a special value? There is.

When resistors are connected in series, the total resistance is simply the sum of the individual resistance values. A typical series connection is shown in Fig. 3 (A). If the resistors shown had values of 500 ohms (R1), 100 ohms (R2) and 50 ohms (R3), the total resistance would be the simple sum of these values:

When resistors are connected in parallel, the total resistance is less than the value of the smallest resistor. A parallel resistor circuit, together with the mathematical formulas used to calculate total resistance, is shown in Fig. 3 (B). Where only two resistors are in parallel, a special, relatively simple formula may be employed. This formula is also given in Fig. 3 (B).

As an example, assume that a 300-ohm and 500-ohm resistor are connected in parallel. Total resistance would then be:

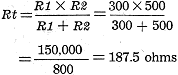
Note that the value obtained (187.5 ohms) is less than that of the smallest resistor in the parallel network (300 ohms).

Where all the resistors are of the same value, the total parallel resistance can be determined simply by dividing the value of one resistor by the number of resistors connected in parallel. For example, suppose there are five (5) one-thousand-ohm (1000-ohm) resistors connected in parallel. Total resistance would be 1000 divided by 5 or 200 ohms.

Fig. 2 - Circuits for assisting in determining the value of the unknown resistor in the following configurations: (A) series healer string. (B) cathode bias. (C) meter multiplier.

When specifying a resistor size, not only the resistance must be known but also the wattage rating. All the resistors which are shown on the facing page have exactly the same resistance value, but there is a big difference in physical size ... and in price as well.

The wattage rating of a resistor is determined by the amount of current it can handle, for its resistance, without overheating or burning out. Thus, it is determined by the power that the resistor can dissipate as heat. Naturally, a large resistor can dissipate more heat than a smaller resistor, and - as would be expected - the larger the wattage rating of a resistor, the larger its physical size.

Actual power, in watts, may be determined by the formulas given in Fig. 3 (C). When choosing a resistor for an electronic application, it is common practice to pick a wattage rating in a standard size at least two to three times the actual wattage that the resistor must dissipate as heat.

As practical examples, let's determine the wattage ratings of the three resistors which were chosen for use as a series filament resistor, as a cathode bias resistor, and as a meter multiplier resistor in the previous examples.

Series Resistor: In the circuit given in Fig. 2(A), it was decided to use a 150-ohm resistor. To determine the wattage rating, the actual power dissipation must first be determined, using the first formula given in Fig. 3(C) :

Twice this value would be around 7 watts, and the next standard resistor size is 10 watts. Therefore, in this application, a 150-ohm, 10-watt resistor would be specified.

Cathode Resistor: In the second example, using the circuit given in Fig. 2(B), it was determined that a cathode resistor of 150 ohms would be needed to give a bias voltage of -7.5 volts with a cathode current of 53 ma. Let's round off the current figure to 50 ma. ... the results will be close enough for practical design work. Using the last formula given in Fig. 3(C), and changing 50 ma. to 0.050 ampere, the actual power dissipation would be:

Fig. 3 - (A) series resistors; (B) parallel resistors; (C) equations for calculating power.

Multiplier Resistor: In the third example discussed, Fig. 2(C), it was calculated that a 100,000-ohm resistor would be needed as a meter multiplier to change an 0-1 ma. meter to a 0-100 volt voltmeter. Wattage? Let's use the second formula given in Fig. 3C.

And, in this case, a 1/2-watt or even a 1/4-watt resistor would be satisfactory.

In this discussion, the value of learning and using Ohm's law to the average experimenter has been emphasized. Remember, however, if these problems and examples seemed a little difficult, that they were so only because of unfamiliarity with Ohm's law. As practice and experience are gained, calculating resistor values with Ohm's law becomes easier and easier ... the stage can be reached where most of the calculations are performed mentally, with pencil and paper seldom being necessary.

But one thing is certain! Learning to use and to apply Ohm's law will result in a better understanding of circuit action, making it possible to undertake and to complete successfully a greater number of projects. It will also enable the experimenter to enjoy his hobby a lot more!

How to Use Ohm's LawFebruary 1956 Popular Electronics

How to Use Ohm's Law
February 1956 Popular Electronics