July 1966 QST
 Table
of Contents Table
of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
The term "modern" in the title of any book
or article never has set right with me because it is utterly ambiguous about the
era to which "modern" refers. Sure, it sounds good at the time, but when applied
to this 1966 QST article, "modern" should be replaced with "four-decade-old." However,
in this case the content is still relevant even thought it was written so long ago
(or else I would not be reproducing it here). It may well have been most people's
first exposure to elliptical (Cauer) filters. As you might
expect, the rigorous, headache-inducing mathematics is omitted, but the article
does give an example of implementing an audio frequency bandpass filter by cascading
a lowpass filter and a highpass filter. If you are familiar with filter design,
you know that because of phasing and inband impedance mismatch issues you cannot
simply butt the two together to yield an equivalent bandpass filter. In fact, the
author found it necessary to insert a 13 dB attenuator between them in order
to get acceptable performance.
An Amateur Application of Modern Filter Design
By Edward E. Wetherhold, * W3NQN

Completed speech filter, less cover, showing the component mounting
boards and front panel with bypass switch and microphone connectors. The low-pass
filter components, marked with the 3-kc. cutoff values, are mounted on the top phenolic
component mounting board. The transistor amplifier is mounted on the bottom phenolic
board, the high-pass filter with the resistor pad on the middle board. Note the
phenolic washers used to hold the 60- and 88-mH. toroids firmly in place.
The method of filter design known as "modern network synthesis" leads either
to simpler circuits for a given performance or improved performance for a given
degree of circuit complexity, as compared with the longer-established design procedures.
Here the author uses the system to come up with a simplified "Filterfier" plus a
design for an accompanying high-pass filter.
Low- and High-Pass Audio Filters for Shaping Response
Over the past several years, there has been a major revolution in the design
of electric wave filters. The old image-parameter approach developed by Campbell
and Zobel1 in the early 1920s with the now-familiar terminology of "characteristic
impedance," "constant-k section," and "m-derived section" has finally been superseded
by a vastly superior filter-design method generally known as "modern network synthesis."
Although this method is not new, having been first mentioned in 1929 and later expanded
during 1940-19502, it was not practical to apply it to practical filter
problems until the digital computer became available as a design tool. The recent
publication of two texts3,4 with design tables derived by the computer
now makes it possible for the progressive radio amateur to take advantage of this
most recent development in filter design.
The fact that many radio amateurs apparently are not yet aware of the advantages
of modern filter design techniques is indicated by recent articles5,6
in which the now-passé image-parameter design approach was employed. The
purpose of this article is to illustrate an application of modern design to a simple
filter problem already "solved" by the image-parameter filter. By comparing the
performance and components of the filters that result from these two different approaches,
the degree of superiority and advantages of the modern filter over the image-parameter
filter should be evident.

Table 1 - Dual-section elliptical-function lowpass filter.

Table 2 - Single-section elliptical-function highpass filter.
The most recent image-parameter design conveniently accessible to QST readers
is the"Filterfier6," a low-pass filter
designed to be used with s.s.b, phasing-type exciters to restrict the speech frequency
range to that at which the phasing network performs best (approximately 300-3000
c.p.s.), to reduce the possibility of generating unwanted side frequencies in excess
of 3 kc. This was accomplished by choosing a cutoff frequency of 2.40 kc. and designing
an m-derived, constant-k image-parameter filter which produced 37 db. of attenuation
at 3.0 kc. At higher frequencies, the attenuation in the stop band was never less
than 39 db. The filter required four readily-available inductors and seven capacitors
and was designed to be terminated in equal resistances of 1106 ohms.
Desired performance requirements for the comparative low-pass modern filter design
therefore were as follows:
1) A cutoff frequency of 2.4 kc. to permit ease of performance comparison with
the image-design filter.
2) An attenuation of at least 37 db. at 3.0 kc.
3) A minimum attenuation in the stop band of approximately 39 db.
4) Equal source and load resistances of approximately 1000 ohms.
It was also desirable to utilize the currently-available 88-mH. toroidal inductors
because of their high Q and very low cost.7
Modern Filter Design Applied to the Filterfier
With these thoughts in mind, a filter type classified by the filter theorists
as a "dual-section elliptic function" was chosen as being most suitable for this
particular application. From the many possible variations available in the computer-derived
tables of Geffe's book'' for the elliptic-function type, one was chosen which best
approximated the desired performance requirements. The tabulated computer-derived
design parameters, all normalized for a cutoff frequency of 1 radian/sec. and 1-ohm
resistance terminations, were scaled to the desired levels simply by multiplying
all normalized values by the proper factors. Normalized frequencies were scaled
by multiplying them by the cutoff frequency in kilocycles. Component values were
scaled by multiplying all capacitances by 1/Rω and inductances by R/ω,
where ω is
2πƒco. The source and load resistances,
R, were specifically chosen to assure that the higher inductance required by the
filter would be 88 mH. The lower inductance came out to be 60.3 mH. The filter values
associated with cutoff frequencies of 2.40 kc. and 3.0 kc. are presented in Table
I. The second cutoff frequency of 3.0 kc. is presented as an alternate for those
who may prefer a wider passband for their particular application. Note that the
same inductance values are required, but the source and load values are different
as are also the capacitance values.
The toroidal inductor used has two separate 22-mH. windings on a toroidal core.
When the windings are connected in series aiding, the total inductance is 88 mH.
with a Q of 45 at 1 kc. One of these inductors is used in its unmodified form for
L2. A second 88-mH. toroid is modified
by removing 62 turns from each 22-mH. winding so that when the modified coils are
connected in series aiding, the resulting inductance is 60 mH., which is the amount
of inductance required for L4.
Mylar capacitors were used because of their small size, low loss and excellent
capacitance stability relative to change of temperature and time. The capacitances
of a large number of Mylar capacitors were measured with an impedance bridge and
the true value marked on each capacitor case. Appropriate values were then selected
and paralleled to produce the capacitances of C1
through C5 to within ±2 percent
of the value specified in Table I. The two toroids and associated capacitors were
mounted on a phenolic board 2-7/16 by 3-5/8 by 1/16 inch thick and wired according
to the low-pass filter schematic of Table I. This completed the filter construction.
Filter Response Evaluation and Performance
The completed filter was subjected to a transmission-loss response evaluation,
the results of which are shown in Fig. 1. Transmission-loss response is defined
as the ratio of the voltage amplitude V1
of the load signal before filter insertion to the value of load signal V2 at the filter output terminals after insertion
of the filter. This ratio is generally expressed in decibels.

Fig. 1 - Transmission loss vs. frequency, low-pass filter
with 2.4·kc. cutoff using the values shown in Table I. Peak rejection frequencies
are 3.14 kc. (ƒ004) and 4.51 kc. (ƒ002).

Fig. 2 - Transmission loss vs. frequency, low-pass filter
with 3.0.kc. cutoff using the values shown in Table I. Peak rejection frequencies
are 3.92 kc. (ƒ004) and 5.63 kc. (ƒ002).

Another view of the filter, showing the back side of the front
panel. The input transformer is clearly visible in this view.
A Heathkit Audio Generator, Model AG-9 (step-frequency type) was calibrated against
a digital frequency counter to provide known test frequencies to better than 1-percent
accuracy. Input and output voltage amplitudes were measured with a Heathkit a.c.
v.t.v.m., Model AV-2. Resistive terminations, as specified in Table I, were provided
for the filter input and output.
The response curve shows two" ripples" in the filter passband of less than 1
db., which is sufficiently in accord with the expected maximum passband attenuation
of 0.5 db. The two passband ripples are typical of the dual-elliptic-type filter.
The measured cutoff frequency occurs at 2.40 kc. where the response curve continues
rising above the level of the maximum passband attenuation. The remainder of the
filter performance is equally in accord with the design specifications.
Comparing the response curve of the modern filter with that of the image filter
(Fig. 3, page 33, November 1965 QST), no outstanding differences are noted
above 1 kc. However, in comparing the two filter circuits, the modern filter design
requires significantly fewer components - only two inductors and five capacitive
elements compared to four inductors and seven capacitive elements. Another advantage
of the modern design not immediately obvious is the fact that the transmission loss
in the modern filter passband is less than 1 db. whereas the image design used in
the Filterfier has a loss in excess of 6 db. as a result of the 660 (640)-ohm resistor
separating the m-derived section from the constant-k section. If it is desired to
install the modern filter in the Filterfier circuit, it is only necessary to provide
the required filter source and load resistances of 1305 ohms or 1630 ohms, depending
on whether the 2.4-kc. or 3.0-kc. cutoff filter is used.
Bandpass Speech Filter Using Modern Filter Design
Because the results of applying modern filter design techniques to the low-pass
filter application were so successful, it was decided also to design and construct
a high-pass filter so that, in combination, the two filters would provide a bandpass
of 300-3000 c.p.s. The bandpass filter is intended to be used with an active device
that will be inserted between a microphone and speech input amplifier so as to provide
approximately unity gain. The component values and other associated information
for the 3.0-kc. low-pass filter are presented in Table I. The transmission-loss
response curve is shown in Fig. 2.
Considerations for the design of the high-pass filter were that, for simplicity,
only one toroid be required, the minimum attenuation in the stop band be 20 db.,
and that maximum pass-band ripple be 0.5 db. The most suitable compromise appeared
to be a design which required two 0.1-µf. capacitors, one 0.235-µf.
capacitor and one 3.11-henry toroid for source and load impedances of 4260 ohms.
See Table II for filter parameters and schematic. With these component values, the
cutoff frequency was 294 c.p.s. and the resonant frequency of the series-tuned circuit
was 186 c.p.s. The cutoff frequency and impedance level were deliberately juggled
to make C1 and C3 come out to a nice even 0.10 µf. The 3.11-henry
toroid uses a core of Permalloy and has a Q of 50 at 1 kc., or approximately 15
at the ƒco of 294 c.p.s. The filter
was assembled, evaluated and found to perform satisfactorily in every respect. The
next step was to cascade the low-pass and high-pass filters to form the desired
bandpass filter.
Cascading the Low-Pass and High-Pass Filters
A 13-db. pad was installed between the high-and low-pass filters to provide impedance
matching and also some degree of isolation. The cascaded filters and pad were then
evaluated for relative attenuation vs. frequency, using the test circuit shown in
Fig. 3. The response curve is also presented in Fig. 3. The high-pass
filter was purposely placed after the low-pass filter so as to attenuate any 60-cycle
hum that might be picked up by the low-pass filter. The output of the high-pass
filter is terminated in its specified load impedance of 4300 ohms. Since the filter
is designed to work into the input resistor of a microphone preamplifier, which
is generally in excess of 1 megohm, the filter load termination of 4300 ohms will
be relatively unaffected by connection to the speech preamplifier. In fact, if a
volume control is desired a 5000-ohm potentiometer shunted by 30,000 ohms could
be used as the high-pass filter load with the potentiometer arm wired to the output
connector.
Transistor Amplifier Design
To overcome the losses in the resistive filter matching pad and input matching
transformer, an amplifier voltage gain of approximately 40 db. was required. Also,
a low-impedance source was required to drive the filter input for best results.
The required gain was obtained from a common-emitter transistor stage with a voltage
gain of between 100 and 150. Using the input transformer specified in Fig. 4,
an input impedance of about 300,000 ohms is anticipated, which should be sufficient
to assure a flat response down to 300 c.p.s. even if a crystal microphone is used.
The low-impedance signal source for the filter is provided by a common-collector
stage which is direct-coupled from the common-emitter amplifier stage, thus eliminating
the necessity for a coupling capacitor and bias resistors. The output impedance
of the common-collector stage is approximately 40 ohms. Placing a 1600-ohm 5 percent
resistor between the emitter follower and low-pass filter very nicely solves the
matching problem.
The transistors, manufactured by General Electric and available from Allied Radio
Corp. for about 80 cents each, are n-p-n silicon planar passivated types specifically
designed for low-level audio applications. The input transistor, a 2N3391A, has
a controlled noise figure and high beta and so is very well suited to its application
in this design. The 2N3392 is similar but has a lower beta and no specification
regarding noise figure.
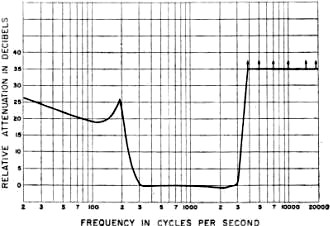
Fig. 3 - Relative attenuation vs. frequency, cascaded low-pass
and high-pass filters. Insertion loss due to matching pad is 13 db. Arrows indicate
attenuation in excess of measurement capability of equipment.

Cascading the Low-Pass and High-Pass Filters
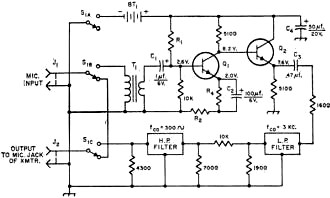

Fig.4 - Circuit diagram of the bandpass speech filter. Resistances
are in ohms, K = 1000; resistors are 1/2·watt, 5 percent tolerance.
Several combinations of parallel resistors were installed for R1 until
a Q1 emitter current of 1.3 ma. was obtained. In this particular case,
the required resistance for R1 was 44,000 ohms. Switch S1,
which simultaneously bypasses the entire circuit and also switches out the battery,
was provided as a convenient means to permit comparison of the modulated transmitter
output with and without the bandpass speech filter. With an operating duty cycle
of 2 hours per day, the useful life of the 15-volt battery may be expected to be
in excess of one month. If it is desired to omit the resistive pad and the high-pass
filter, simply terminate the low-pass filter with a 1600-ohm resistor, change R4
to 1300 ohms, and if R2 is made 220 ohms unity gain should be approximated.
Components
The desired filter performance will be assured if reactors with a ±2 percent
tolerance, resistive terminations with a ±5 percent tolerance, and inductors with
as high a Q as practical are used. There will be relatively little difficulty and
expense in obtaining the 88- and 60-mH. inductors. However, obtaining the 2 percent
capacitors will require some extra effort. Also, the 3. 1-henry toroid may prove
to be more expensive than anticipated. This toroid is available from the Allen Organ
Co. (3.11 henry, ±2 percent, Q = 50 at 1 kc.) at a cost of $1.43 each with a minimum
billing charge of $20. An alternate source is Newark Electronics Corp. (Stock No.
39F2806, Collins toroid type MP-930-37B, 3.0 henry, ±1 percent, Q = 58 at 1.5 kc.)
at a cost of $7.23. The author employed the following procedure: Mylar capacitor
and Allen toroid data sheets were requested from the Components Division of Allen
Organ Co., Macungie, Pa., and $20 worth of Mylar capacitors and permalloy toroids
was selected and ordered. The capacitor cost ranged from 13 cents for 0.007 µf.
to 17 cents for 0.10 µf., and about fifty capacitors of mixed values were
obtained for $8. The remainder of the $20 was invested in toroids, one of which
was the 3.11-henry value. An impedance bridge was borrowed and all the capacitors
were measured to an accuracy of 2 percent or better and the values marked on the
capacitor cases. Appropriate values were then selected and paralleled to produce
the desired filter capacitance values.
Performance of the Completed Unit
When first tested, the gain of the bandpass speech filter was found to be greater
than unity by 4.5 db. R2 was added to the circuit and adjusted until
the desired unity gain was achieved. The 3.1-henry toroid in the high-pass filter
was found to be sensitive to hum pickup, and therefore the filter should not be
placed in the immediate vicinity of power transformers. The overall frequency response
of the entire unit was found to he essentially the same as that of Fig. 3 except
that the attenuation was greater than indicated by the response curve at frequencies
below 100 c.p.s., because of the roll-off effects of C3 and possibly
T1. An operational check of the filter on the air was satisfactory in
every respect.
Acknowledgments
The author wishes to thank John Brennan, Jr. for providing the photographs, Tom
Miller, W7QWH/3, for performing the operational checkout, and Millicent Schaffer
for typing the manuscript.
* Dept. 2N, Electro International, Inc., Box 391, Annapolis, Md. 21404
1 Zobel, "Theory & Design of Electric Wave Filters," The Bell
System Technical Journal, January. 1923. 2 Zverev, "Introduction
to Filters," Electro-Technology, June,1964. 3 Geffe, Simplified Modern
Filter Desiqn, John F. Rider Publisher, Inc., New York City, 1963. 4
A Handbook on Electrical Filters, published by White Electromagnetics, Inc., Rockville,
Maryland, 1963. 5 Genaille, "Low-Pass
Audio Filters for Increased Talk Power," Electronics World, September, 1963.
6 MacCluer and Thompson, Jr., "The Filterfier,"
QST, November, 1965. 7 For example,
88- and 44-mH. toroids are available 5 for $1.75, postpaid, from Buchanan &
Associates, 1067 Mandana Blvd., Oakland, California 94610.
Posted March 10, 2020
(updated from original post on 2/12/2013)
|