February 1945 QST
 Table
of Contents Table
of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
In 1945, when this article was published
in QST magazine, radar was still in its infancy. Engineers were already
aware of the need to shape pulse waveforms from experience with CW keying and
the need to mitigate the effects of "chirping." A perfectly rectangular pulse
in the time domain, as we learned in our signals and systems courses, creates
a sin (x)/x response
in the frequency domain. The Fourier transform shows that a perfectly square
pulse in the time domain is the summation of an infinite number of odd harmonics
of the fundamental (1st harmonic). The first few harmonics are audible to the
CW copier as higher frequency "chirps." To reduce the annoyance (and wasted
transmitted energy), time constants were added to the leading and trailing edges
of the waveform to remove the higher frequencies, while leaving the pulse shape
sufficiently rectangular to achieve its goal. The same type issue applies to
radar pulses.
Bandwidth Requirements for Pulse-Type Transmissions

Fig. 1- Graph of modulation envelope with pulse. type
transmission.
A Discussions of Wave Shape as a Guide in Frequency Allocations
By W. W. Hansen (Research Engineer, Sperry Gyroscope Co., Inc., Garden City,
N.Y.)
IN MAKING suggestions as to suitable allocations of wave bands in the microwave
region for the future, due caution should be exercised in considering any proposed
system which uses grossly more bandwidth than the minimum required by the information
communicated.
It may be that wave bands can be allotted more liberally in the microwave
region than in the long-wave region, simply because there is so much band space
available that it is difficult to see at present how all of it can be used.
Nevertheless, the history of the spark transmitter suggests that caution is
in order; at least serious thought should be given before systems using excessive
spectrum space are permitted. It is the object of this article to present some
information relative to one family of such systems and to make some suggestions
as to possible regulations which might usefully be imposed on such types of
transmissions.
Modulating Systems
Pulse technique in which the carrier is broken up at regular intervals before
modulation probably is one of the most important radio developments since the
beginning of the war. lts possible applications still are far from being fully
explored. While it is apparent that greater band-widths are required for transmissions
of this type, certain advantages may be gained if it is possible to operate
under conditions where band-width is not of too great importance. This, of
course, points to applications which make use of much higher frequencies than
those heretofore employed by amateurs. Among the advantages claimed for pulse-type
transmissions are a considerable improvement, in signal-to-noise ratio and
the simplification of equipment. Since there may be ways in which this technique
can be used to advantage in amateur work of the future, this discussion of
pulse shape in relation to spectrum economy should be of unusual interest.
The type of systems we have in mind perhaps may be illustrated by means of
an example. Suppose the information we wish to transmit has frequencies up to
10 kc. Then assume that we choose some higher frequency, say 20 kc. as a "subcarrier."
The transmitter then is turned on and off at a 20-kc. rate. This is called discontinuous
modulation. When the signal input voltage is zero, the transmitter is on half
the time and off half the time. In other words, the microwave modulation envelope
is a 20-kc. square wave with equal" on" and "off" periods. Then to modulate
upward, one increases the time the transmitter is on and decreases the time
it is off, 100 percent modulation occurring when the transmitter is on continuously.
To modulate downward, one decreases the fraction of the time the transmitter
is on. More generally, the unmodulated condition can correspond to the transmitter
being on less (or more) than half the time. For example, one microsecond pulses
at a rate of 1000 pulses per second might correspond to no modulation and two-microsecond
pulses to 100 percent upward modulation. Another possible system is one having
all pulses of the same duration but varying in the number per second in accordance
with the information-bearing modulation. Still another method would be to vary
the phase of the pulses in accordance with the signal modulation.
The advantage of such systems is that they will work with power sources that
cannot be modulated linearly in a continuous manner. Another point is that a
great deal of suitable technique is available as a result of war-inspired research.
Incidentally, one of these systems was used in the early microwave link across
the English channel developed by I.T.T. about ten years ago.
Pulse Shapes
Let us now inquire into the frequency spectrum required by such a system.
Fundamental to the problem is the frequency spectrum corresponding to a single
typical pulse. This depends, of course, upon the shape of the pulse. We shall
give results for two pulse shapes which, it would seem, constitute a sort of
upper and lower boundary for pulses which may be realized in practice.
Consider first, then, a simple flat-topped pulse of duration to.
The frequency spectrum corresponding to this pulse is  and the distance
between 71-percent points on a frequency scale is easily found to be 0.88/to.
While the distance between 71-percent points is a good measure of the frequency
interval containing most of the energy, it should be noted that the above function
drops off rather slowly with ω so that considerable intensity exists at high
values of ω. Specifically the envelope of the function is 1/πft0 so that, for example,
when f is 10 times the value corresponding to the 71-percent point,
the amplitude is down only about fourteen times near one of the peaks of and the distance
between 71-percent points on a frequency scale is easily found to be 0.88/to.
While the distance between 71-percent points is a good measure of the frequency
interval containing most of the energy, it should be noted that the above function
drops off rather slowly with ω so that considerable intensity exists at high
values of ω. Specifically the envelope of the function is 1/πft0 so that, for example,
when f is 10 times the value corresponding to the 71-percent point,
the amplitude is down only about fourteen times near one of the peaks of  . In this matter of
a rather slow decrease of amplitude with increasing w, the flat-topped pulse
is the worst function likely to be encountered in practice. . In this matter of
a rather slow decrease of amplitude with increasing w, the flat-topped pulse
is the worst function likely to be encountered in practice.
Consider next a pulse in the form  the numerical factor being so chosen that the time
between 71-percent points is to. Then one finds the frequency spectrum to be
of the form the numerical factor being so chosen that the time
between 71-percent points is to. Then one finds the frequency spectrum to be
of the form 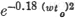 and from this we find the separation of the 71-percent
points on frequency to be 0.44/to. Also, at a frequency ten times
the frequency at the 71-percent point the function is down by about 15 powers
of ten or 300 decibels in power. This is to be compared with 26 decibels for
the square pulse. and from this we find the separation of the 71-percent
points on frequency to be 0.44/to. Also, at a frequency ten times
the frequency at the 71-percent point the function is down by about 15 powers
of ten or 300 decibels in power. This is to be compared with 26 decibels for
the square pulse.
Actual pulse forms which may be used will fall between the above two limits.
The frequency spectrum cannot fall off as slowly as that first considered, because
the start and finish of the pulse cannot be perfectly abrupt, as assumed. On
the other hand, a pulse as smooth as the Gauss-error type discussed above is
not likely in practice.
Pulse Modulation
Next, what happens if a series of pulses is used to modulate a carrier? If
they are evenly spaced and of uniform intensity, as we shall assume for a moment,
then the frequency spectrum is as illustrated qualitatively in the graph of
Fig. 1 which is drawn for the Gauss-error-curve type of pulse.
Here the origin corresponds to the carrier frequency and the various peaks
are spaced f1 apart, where f1 is the
subcarrier frequency. The dotted line, which is the envelope, has the same shape
as the spectrum of a single pulse. Strictly speaking, the various peaks, which
have been drawn with a small but finite width, should be infinitely narrow and
infinitely high but with a finite area corresponding to the dotted-envelope
curve.
If, finally, we vary the height of the various pulses according to some signal
voltage, each peak spreads out to a width corresponding to the frequencies contained
in the signal voltage. We will call the highest frequency contained in the signal
voltage f2.
Band-Width Requirements
Actually, the modulation is not done by varying the height, but the width
or the frequency or the phase of the pulses. This complicates the analysis too
much for discussion here but one point, and it is the essential one, remains
unchanged. Namely, the frequency spectrum follows roughly the spectrum corresponding
to a single pulse; or, stated more exactly, the envelope of the frequency spectrum
follows the spectrum of a single pulse.
From the above we see that the amount of spectrum used is of the order of
1/to, whereas one could transmit the information with a band 2f2
(or f2, if a single-sideband transmission were used). Thus,
one uses roughly 1/f2to times as much spectrum
as need be.
How big is this factor?
If one makes the subcarrier, f, only slightly greater than f2
and makes to = 1/2f1 (i.e, uses a square wave
as an unmodulated signal), then the factor 1/f2to
is not significantly different from two, and there is little, if any, waste
of frequency spectrum. (This statement will be subject to some qualification
later.) If, on the other hand, for some reason to is made quite small, say,
for example 10-6 seconds, while f2 is, say 104 cycles per
second, then one uses about 100 times more spectrum than necessary.
In some cases some of this waste can be recovered while still using the same
general scheme of modulation. For example, a number of stations can be assigned
the same carrier frequency provided they are assigned different subcarriers.
Then a band-pass filter in the receiver will separate the signals from various
transmitters.
Interference Capability
In the above we have considered the band used as that between the 71-percent
points. But, although most of the energy usually will lie in this region, this
is not the whole story when it comes to interference. What we want to know is
over how wide a band will there be enough energy to cause interference. Plainly,
this is a question which is difficult to answer quantitatively. Besides the
obvious arbitrariness involved in deciding how much energy will cause interference,
etc., there is the very important matter of pulse shape. Indeed, as the calculations
above show, this is probably the most important single factor. Thus, whereas
a smooth pulse of Gauss-error form of about one microsecond duration will cause
no appreciable interference outside a band a megacycle or two wide, a flat-topped
pulse with perfectly square corners would cause interference that would probably
be called important over 20 Mc. or more.
What conclusions are to be drawn from the above? There follow certain suggestions
and opinions of the author which may form a partial answer to this question.
If the subcarrier frequency is not much higher than the highest information
frequency and the average pulse length not much shorter than a half cycle of
the subcarrier frequency, there is no essential waste of frequency spectrum.
But to avoid interference because of tails of the frequency spectrum, the regulations
should call for some means of reducing the harmonics of the sub-carrier frequency;
in other words, rounding the corners of the pulses. Some ideas on this point
will be suggested later.
If the pulse length is markedly short compared to the reciprocal of the highest
information frequency, necessarily there is a waste of frequency spectrum, unless
the purpose is multiplex transmission, and it should be considered carefully
whether this is warranted. For example, with one microsecond pulses, there would
be room for rather less than 300 stations between 9 cm. and 10 cm. In the author's
opinion, probably there are enough available frequencies to allow such waste,
provided certain conditions are imposed.
Use of Filters
Some means must be provided to round the corners of the transmitted pulses,
as mentioned before, so avoiding an additional wastage of frequency spectrum
by a factor which may amount to ten or more. Rounding the corners of the d.c.
voltage pulse will not be permissible in some cases, since many of the tubes
on which this system will be used have a strong tendency toward frequency modulation.
Besides, this defeats the main purpose of discontinuous modulation. The simplest
and best method would appear to be the requirement of a filter in the antenna
line. This appears to be a thoroughly practical scheme. For example, with one-microsecond
pulses one could use one or more resonators with bandwidths of about one megacycle
between the transmitter and the antenna. How many stages of filter should be
required is a question to be answered by the conditions prevailing in each case.
The author would suggest that two would be sufficient in most cases.
Conclusions
Use of the modulation system suggested should be confined to certain restricted
bands, leaving other bands where more normal systems will be free from what
might perhaps be styled "super monkey chatter." This should present no difficulty
since advocates of this system will no doubt claim that it does not cause undue
interference. They should, therefore, be quite pleased to have various interference-free
regions of the spectrum to themselves.
Finally, the author would like to add that almost all the above applies to
pulsed radar sys-tems, except that in this case the use of short pulses is often
a real necessity, not a matter of real or fancied convenience. In the author's
opinion much trouble would be avoided if all pulse systems were put in a segregated
band, and if output filters to cut off the frequency tails were required. As
to the first, there is certainly no reason to burden television and other communications
services using continuous modulation with the difficult problem of putting up
with pulse interference caused by discontinuous modulation. As to the second,
such filters need not interfere with the performance of a system. They are cheap
and easy to apply, and will greatly reduce interference potentialities.
Posted January 22, 2021
(updated from original post on 6/23/2011)
|






 and the distance
between 71-percent points on a frequency scale is easily found to be 0.88/to.
While the distance between 71-percent points is a good measure of the frequency
interval containing most of the energy, it should be noted that the above function
drops off rather slowly with ω so that considerable intensity exists at high
values of ω. Specifically the envelope of the function is 1/
and the distance
between 71-percent points on a frequency scale is easily found to be 0.88/to.
While the distance between 71-percent points is a good measure of the frequency
interval containing most of the energy, it should be noted that the above function
drops off rather slowly with ω so that considerable intensity exists at high
values of ω. Specifically the envelope of the function is 1/ the numerical factor being so chosen that the time
between 71-percent points is to. Then one finds the frequency spectrum to be
of the form
the numerical factor being so chosen that the time
between 71-percent points is to. Then one finds the frequency spectrum to be
of the form 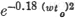 and from this we find the separation of the 71-percent
points on frequency to be 0.44/to. Also, at a frequency ten times
the frequency at the 71-percent point the function is down by about 15 powers
of ten or 300 decibels in power. This is to be compared with 26 decibels for
the square pulse.
and from this we find the separation of the 71-percent
points on frequency to be 0.44/to. Also, at a frequency ten times
the frequency at the 71-percent point the function is down by about 15 powers
of ten or 300 decibels in power. This is to be compared with 26 decibels for
the square pulse. 


