|
June 1953 QST
 Table of Contents Table of Contents
Wax nostalgic about and learn from the history of early electronics. See articles
from
QST, published December 1915 - present (visit ARRL
for info). All copyrights hereby acknowledged.
|
If you have ever heard the audible hum emitted
by a power supply transformer, then you are familiar with at least one of the manifestations
of magnetostrictive
materials. I thought maybe shape memory metals ("muscle wire")
would be considered magnetostrictive, but research shows they are classified separately
because their shape change is attributed primarily to heating rather than magnetization.
I also thought the old 'reeds' type receive decoders for pre-1960s-era radio control
systems might be magnetostrictive devices, but no search turned up anything where
the term was used. This article and its two succeeding articles discuss magnetostrictive
filters at kilohertz IF frequencies. Part I covers the fundamentals of magnetostrictivity
while Part II gets into building realizable bandpass filters. Unfortunately,
I do not have the August 1953 edition of QST for Part III. The referenced article
in the
September, 1950, issue of the RCA Review was located on the American Radio History
website, for those wanting to know more about the subject.
Magnetostriction Devices and Mechanical Filters for Radio Frequencies
Part I - Magnetostriction Resonators (see
Part II)
By Walter Van B. Roberts, W2CHO
Recent developments in the field of mechanical resonators may foreshadow increasing
applications in our amateur gear, especially in high-selectivity receivers and single-sideband
filters. This is a "get-acquainted" article, outlining the principles of magnetostrictive
and mechanical resonators and showing how they are applied. There is plenty in this
and in subsequent parts of this article to whet the experimenter's appetite - especially
since some of the currently hard-to-get materials may be more readily available
in the near future.
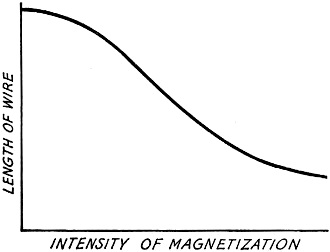
Fig. 1 - Form of length vs. magnetization curve for nickel.
Iron is, of course, the most commonly used magnetic material. But nickel is also
strongly magnetic, as is easily seen by the way it sticks to a magnet. In addition,
nickel is relatively strongly magnetostrictive; that is, the length of a piece of
nickel will change when it is magnetized. The actual amount of change is very small,
not over one part in 20,000, but even this small amount is large compared with what
is found in most magnetic materials, and is sufficient to be put to practical use.
Fig. 1 shows how the length of a piece of nickel wire varies with its magnetization.
The same sort of curve applies to other magnetostrictive materials, except that
the amount of change is usually much smaller and some materials lengthen instead
of shrinking when magnetized.
Fig. 2 shows how mechanical vibrations can be produced in a nickel wire
by means of magnetostriction. The permanent magnet is placed near enough to the
wire to cause it to shrink about half the maximum possible amount. Then when current
flows in the coil it will either decrease or further increase the amount of shrinkage,
depending on whether the magnetizing effect of the coil opposes or aids the field
of the magnet. If the current is alternating, the length of the wire will vary at
the frequency of the current. The constant field of the magnet will be called the
magnetic bias, and the field of the coil will be called the driving field. (The
bias could also be produced by a d.c. component of current in the coil, or by permanent
magnetization of the nickel.) Thus, the magnetic bias and the driving field correspond
somewhat to the voltage bias and signal voltage on the grid of an amplifier tube.
If the frequency of the driving field is not near the natural frequency of vibration
of the wire, the variation in the wire length will be extremely small, but if the
piece of wire in Fig. 2 is one inch long and the frequency of the driving current
is about 100 kc., a much greater amplitude of vibration occurs. The one-inch length
of wire has a natural frequency of longitudinal vibration at about 100 kc. When
the driving-current frequency is made to match the mechanical resonance of the wire,
considerable mechanical power is transferred to the wire and the vibration of the
wire reacts upon the driving coil just as though the wire were a sharply tuned electrical
circuit loosely coupled to the driving coil. This reaction can be observed by connecting
the driving coil to a Q-meter. Then when the frequency of the Q-meter is slowly
shifted through the resonant frequency of the wire, the apparent Q of the coil takes
a sharp dip. The sharpness of the dip depends on the mechanical Q of the wire resonator.

Fig. 2 - Longitudinal type magnetostriction resonator.

Fig. 3 - Q-meter response as the driving frequency to a pair of coupled
circuits, both tuned to the same frequency, fo is varied. The peak separation increases
with the coefficient of coupling.
The term "mechanical Q," as applied to a mechanical resonator, means the number
of cycles of vibration required for the amplitude to die down to 4.32 per cent of
its original amplitude after the driving force is removed. (This same definition
applies to the Q of a tuned circuit). In general, the Q of a mechanical resonator
is much higher than that of the best tuned circuits and this is one of the great
advantages of mechanical resonators.
Ferrite Resonators
The use of nickel and other metal rod resonators in the manner illustrated in
Fig. 2 is nothing new, but has not been very widespread because resonator materials
known heretofore have been metallic and hence cause large eddy current losses which
spoil the Q of the driving coil. Also, the mechanical Q of a nickel resonator is
only a few hundred. (Many metals have mechanical Qs up to ten thousand, but are
not magnetostrictive). There has recently become available, however, a new group
of magnetic materials, called ferrites, that are much better adapted to magnetostrictive
resonator use. Ferrites are more in the nature of ceramics than metals, and may
have high electrical resistivity so that eddy-current losses are negligible. Their
mechanical Q is of the order of several thousand, and some are strongly magnetostrictive.
Their permeability is usually high and when a ferrite resonator is put in a coil
it may greatly increase the Q of the coil itself. The longitudinal vibration frequency
of a ferrite rod is about 103 kc, divided by the length of the rod in inches.
Ferrites are made by mixing powdered Fe2O3 with various
proportions of other metallic oxides, pressing to the desired shape, and firing
at 1300 to 1400 degrees C. The mix can also be extruded in the form of rods or tubes.
After firing, it is too hard and brittle to machine. It can be ground or cut with
a diamond saw. The permeability, magnetostrictive activity, and improvement of coil
Q are determined by the proportions of the oxides forming the ferrite. No one composition
makes all these quantities maximum; the composition to use depends upon the job
it has to do. A good magnetostrictive ferrite can be made of "equimolar" proportions
of iron and nickel oxides; i.e., 159.68 grams of Fe2O3 and
74.69 grams of NiO. More detailed information about ferrites may be found in the
September, 1950, issue of the RCA Review.
Coefficient of Coupling

Fig. 4 - Set-up for measuring the coefficient of coupling between a tuned
circuit and a ferrite-rod magnetostriction resonator.

Fig. 5 - The equivalent circuit, B, of a magnetostriction
resonator coupled to a coil.
When two electrical circuits of low losses are tuned to the same frequency (f0)
and coupled together, two resonant frequencies are found in the system. For example,
if one of the circuits consists of a coil and the variable condenser of a Q-meter,
then as the frequency of the Q-meter is varied, two peaks of the meter will occur
as shown in Fig. 3. If the second circuit is sufficiently low-loss, the coefficient
of coupling between the two circuits is given by (f2 - f1)
/ f0.
Now let the second circuit be removed and a ferrite resonator (suitably magnetically
biased) put in the first coil, as shown in Fig. 4. With the coil tuned to the
same frequency (f0) as the resonator, the Q-meter will behave
exactly as before.
Hence, the quantity (f2 - f1) / f0
may be defined as the coefficient of coupling between the coil and the ferrite.
This quantity is a more useful measure of the magnetostrictive activity of the material
for circuit calculations than the "magnetostrictive coefficient," which merely gives
the amount of stretch or shrink in length that can be produced by magnetizing. The
coefficient of coupling can be decreased by removing the resonator more or less
from the coil or by decreasing the bias, but cannot be increased beyond an upper
limit determined by the nature of the material. This limit is of the order of 10
per cent for ordinary coils and ferrites made for good magnetostriction.
From the coefficient of coupling it is easy to show that a coil with a ferrite
resonator in it (Fig. 5A) is equivalent to Fig. 5B. Here L is the inductance
measured at a frequency far from the ferrite resonance and k is the coefficient
of coupling measured as described above. The condenser and resistor give the equivalent
circuit the same frequency and Q as the ferrite resonator.
Ferrite Oscillator

Fig. 6 - Magnetostriction oscillator using a ferrite rod.

Fig. 7 - Method of permanently magnetizing a ferrite torus.
Probably the simplest use of a ferrite resonator is as the frequency control
element of an oscillator. Fig. 6 shows a suitable circuit. In the absence of
vibration of the resonator there is nothing but inductive reactance between P and
ground, and therefore oscillations cannot occur. Just above the resonant frequency
of the ferrite, however, the total effective reactance between P and ground is capacitive
(see Fig. 5B). The circuit will then oscillate if L and C are tuned to the
approximate frequency of the ferrite - that is, provided there are not too few turns
on the ferrite coil, the tube transconductance and coil Q are not too low, and the
coefficient of coupling between the ferrite and its driving coil is not too small.
The cathode resistor provides initial grid bias which makes oscillation start more
easily. The magnetic bias not only affects the ease of starting but will also be
found to have some control over the frequency of oscillation, perhaps to the extent
of a per cent in some cases. With this circuit, oscillations should be obtainable
up to a few hundred kc., using a 6J6 tube running about 2 mils plate current per
plate, even with the ferrite driving coil reduced to a very few turns.
Permanent Bias
A rod of steel or nickel can be permanently magnetized so that it becomes a bar
magnet with north and south poles at its ends. Rods of cobalt ferrite can similarly
be permanently magnetized. Unfortunately, however, the kind of ferrite that has
good magnetostrictive action is demagnetized so easily that the poles at its end,
created by magnetizing the rod, act to demagnetize it as soon as the magnetizing
field is removed. This drawback does not occur when there are no poles developed
by magnetizing. For example, if a ferrite torus (or any piece of ferrite with a
hole in it) has a wire passed through the hole and connected briefly to a battery
of 1 1/2 to 6 volts, as shown in Fig. 7, the ferrite will be magnetized with
closed loops of magnetic flux linking the wire. No free poles are produced so the
magnetization remains and can be used as permanent bias for resonator operation
in the modes of vibration that require a bias of this sort.
To produce permanent circular bias by means of a flash of current requires that
the ferrite have a hole in it. However, it is possible to produce a certain amount
of "circular bias" in a solid piece of ferrite by means of magnets, as shown in
Fig. 8. Here two horseshoe magnets are put together except for a gap that is
considerably smaller than the ferrite to be magnetized. The ferrite is placed against
the gap as shown, then moved away. As a result of the easy saturation of ferrite,
a small permanent circular bias remains. However, it is much better to use the current
method if there is a hole in the ferrite with closed loops of magnetic flux linking
the wire. No free poles are produced so the magnetization remains and can be used
as permanent bias for resonator operation in the modes of vibration that require
a bias of this sort.
To produce permanent circular bias by means of a flash of current requires that
the ferrite have a hole in it. However, it is possible to produce a certain amount
of "circular bias" in a solid piece of ferrite by means of magnets, as shown in
Fig. 8. Here two horseshoe magnets are put together except for a gap that is
considerably smaller than the ferrite to be magnetized. The ferrite is placed against
the gap as shown, then moved away. As a result of the easy saturation of ferrite,
a small permanent circular bias remains. However, it is much better to use the current
method if there is II hole in the ferrite.
Vibrations Using Circular Bias

Fig. 8 - Inducing permanent circular magnetization in a
ferrite cylinder or disk.

Fig. 9 - Transformer-coupled link for coupling to a ferrite
torus.
The simplest type of vibration that uses circular bias is the radial vibration
of a ferrite torus with a toroidal driving winding on it. The flux produced by the
winding alternately adds to and subtracts from the permanent bias flux, thus causing
the circumference of the torus or ring to vary at the frequency of the driving current.
As the circumference varies so must the radius, and the actual motion of all parts
of the ring is in and out from the center. To give an idea of dimensions, a thin
ferrite ring one inch in diameter would resonate in this mode at about 65 kc., and
for other diameters the frequency would be equal to 65 divided by the diameter in
inches.
The maximum possible coefficient of coupling between a tuned circuit and a ferrite
resonator is obtained when the coil is wound toroidally on a radially vibrating
ring and the bias is optimum. A toroidal winding of many turns is a nuisance to
put on, especially since it must not be tight on the ring, which would interfere
with the vibrations. However, a few turns may suffice for some purposes. For example,
oscillations can be produced in the circuit of Fig. 6 if point P is connected
to ground by a single short piece of wire passing through a ferrite ring. This might
be called a "one-turn toroidal winding." Of course, oscillations are obtained more
easily if several turns are used. The effect of a multi turn winding may be obtained
to some extent by transformer action, as shown in Fig. 9. Here a multiturn
winding, consisting of two "pies" on a magnetic core, acts as one winding of the
transformer while a turn or two of wire around the core acts as secondary winding
and is connected to a one-or-more turn toroidal winding on the ferrite resonator
ring, R. This arrangement works very much as if the many turns were wound directly
on the resonator; that is, provided a good high-permeability core is used, such
as a piece of high-permeability ferrite. The core, of course, does not vibrate mechanically;
it acts only in the ordinary way as the core of a transformer.
Crossed Fields
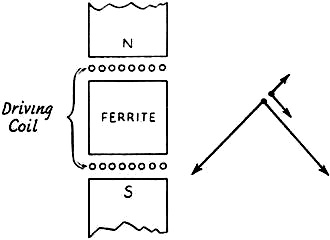
Fig. 10 - Crossed bias and exciting fields result in shear
stresses in a ferrite rod of rectangular form, as shown by the vector diagram at
the right.

Fig. 11 - Coupling to a ferrite cylinder in shear vibration.

Fig 12 - Another type of vibration in a ferrite torus. B and
C show methods of coupling to the vibrator.
So far it has been assumed that the driving flux alternately adds to and subtracts
from the bias flux. What happens if these fluxes are at right angles to each other?
One way to figure this out is to suppose we have a square piece of ferrite with
a bias field across between one pair of opposite edges and a driving field at right
angles, as shown in Fig. 9. The bias field may be represented by a large vertical
vector and the driving field by a small horizontal one. But it is equally possible
to consider the bias vector as composed of two large diagonal vectors and the driving
field as the resultant of two small diagonal vectors, as shown. It is now seen that
along one diagonal the fields aid and along the other diagonal they oppose.
Thus, the effect of the driving field is to distort the square into a slightly
diamond shape. Such a distortion is called a "shear" and the perpendicular arrangement
of bias and driving fluxes can be used to drive resonators whose vibrations set
up shearing stresses. Perhaps the simplest example of such a resonator is a cylinder
or pipe vibrating torsionally; that is, one end rotates one way while the other
end rotates in the opposite direction. The center does not turn but the greatest
shearing stress or twisting force occurs there. Fig. 11 shows a ferrite tube,
permanently biased as previously explained, with a driving coil located over the
node of motion (shown dotted). The frequency of a torsional resonator of this sort
depends only on its length, and for ferrite the frequency in kilocycles is approximately
65 divided by the length in inches. (It is just a coincidence that a magnetostrictive
ferrite has approximately the same frequency for a torsional resonator of length
L as for a radially vibrating ring of diameter L.)
Another example of a vibration mode involving purely shearing stresses is shown
in Fig. 12A. Here the outer portion of a disk rotates in one direction while
the inner portion rotates oppositely. Between these rotations is a ring of no motion
which is called a "nodal ring." This type of vibration might be called concentric
shear because the motions are in concentric circles and the stresses are pure shear.
The frequency depends on the size of the hole. If the hole is very small, the frequency
for a ferrite disk is approximately, in kilocycles, 215 divided by the diameter
of the disk in inches. It will be noted that it is independent of the thickness.
If, on the other hand, the hole occupies most of the disk, the frequency becomes
approximately 131 divided by the difference between outer and inner diameters. Fig. 12B
shows how a flat coil is placed against one side of the disk to drive it in the
concentric shear mode. The dotted line represents a typical line of driving flux.
The bias flux lies in concentric circles within the material, thus being at right
angles to the radial driving flux. A better coupling can be obtained by enclosing
the driving coil in a "pot" of magnetic material, as shown in Fig. 12C, and
a still further improvement should result from using another similar driving system
on the other side of the disk.
[The second part of this article, to appear in a subsequent issue,
will discuss applications of mechanical resonators and the use of ferrites in filters.
- Editor]
Posted January 2, 2020
|







































