Standing Waves on Transmission Lines, December 1942 QST

In this article from a 1942 issue of QST magazine, author T.A. Gadwa employs a standing wave mechanism analogy that I don't recall having read before - that of a dam on a river. The river is the transmission line with a lake as the source (presumably) and then he imagines a dam load. The dam standing waves, per his description, have phase and amplitude characteristics that depend on how tall the dam wall is relative to the surface height of the dammed river. An extensive array of graphs is provided showing how the current of the dam standing waves react to the dam transmission line termination impedance. I always wonder when seeing electrical-mechanical parity examples whether, as with this case, there are any dam magazine articles out there that use an electrical transmission line to help fellow civil engineers understand their dam designs?

Fig. 1 - Section of transmission line with its terminating load.

Standing waves are often a problem to amateurs who attempt to use untuned transmission lines for their antennas. The elimination of these waves is often difficult because of a lack of understanding of the principles involved. Using the analogy of water waves in a canal is often helpful in visualizing the factors that influence the operation of transmission lines. Suppose the canal has a dam at one end and a wave is created at the opposite end. This wave traveling toward the dam is reflected back to the starting point. Now if the height of the dam is lowered sufficiently to allow the initial wave to splash over, then no return wave or reflection is produced. In the radio-frequency application, the canal corresponds to the transmission line and the dam to the load or antenna.

Terman¹ has analyzed the position and magnitude of standing waves on lines for several different types of loads. Everitt² has derived equations that make it possible to establish the character of these waves. If one neglects the line losses, which are usually small for relatively short lengths of line, the calculation is simplified considerably. At radio frequencies, such lines may be assumed to behave as pure resistances. The current at any point on the line for any type of load is given by the equation:

The load may be any of the combinations shown in Fig. 2. The character of the standing waves that are associated with each case will be discussed.

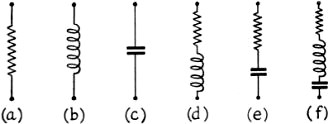
Fig. 2 - Possible combinations of resistance and reactance which may make up the load impedance, Z_r

If a voltage is applied or a current induced at the sending end of a transmission line and the receiving end is an open circuit, a wave traveling toward the open circuit is reflected wholly since no power is absorbed. This reflected wave combines with the incident wave to form standing waves. Waves that can be measured as average values of current or voltage are called standing waves. The readings are all positive since no account is taken of phase between the current and voltage. The results are represented as positive values plotted as ordinates above the horizontal axis. At the open circuit, the voltage is reflected in phase since the incident and reflected voltages are equal and their sum is not zero, while the current is reflected out of phase since the incident and reflected currents are equal and their sum is zero. If the average current or voltage along the line is measured, maxima and minima are found at regular intervals from the receiving end of the line. The current distribution for an open circuit is shown in Fig. 3-1. Only a half wavelength is shown as the cycle is repeated for additional lengths of line. To avoid confusion that might result if voltage were superimposed, only the current wave-forms are plotted. There is always a current minimum or node at the receiving end and at every half-wavelength point back along the line, and a current maximum or loop at every quarter wavelength. Furthermore, the voltage is maximum or a loop at each current minimum or node and there is a voltage minimum or node at each current maximum or loop. It is evident that maximum and minimum values of either voltage or current occur exactly 1/4 wavelength apart.

If the receiving end is short-circuited, a wave starting down the line is reflected and again standing waves are found. Here the positions of the maximum and minimum have been shifted and appear as in Fig. 3-2. At the short circuit, the incident and reflected voltages are out of phase and their sum is zero, while the current is reflected in phase and the sum of the two components is not zero.

If an appropriate pure resistance equal to a constant known as the characteristic impedance of the line is connected as a receiving load, a wave starting down the line is absorbed completely and no reflection is possible. The current and voltage are constant at all points, with no maximum or minimum, as shown in Fig. 3-5. Since all actual lines have losses, the current and voltage diminish slowly toward the load, as indicated in Fig. 3-6. Such lines are known as flat lines. This load impedance is dependent only on the physical properties of the line: the conductor diameter, conductor spacing and type of insulation or dielectric. Its value for an open-air two-wire parallel line is calculated by the formula:

If the load resistance is less than the line impedance but not a short circuit, the standing waves are similar to the short circuit load except that the minimum current is greater than zero, as shown in Fig. 3-4. If the load is made greater than the line impedance but not infinite (open circuited), the standing waves are as shown in Fig. 3-3. It is evident that the maximum and minimum currents occur in the same positions as in the case of the open-circuit load, but the maximum-to-minimum ratio is less. The ratio approaches the value of unity as the load approaches the characteristic impedance.

If the load is an inductive reactance equal to the characteristic impedance, Fig. 2-B, no power is absorbed and standing waves are as shown in Fig. 3-9. The line behaves similarly to a short-circuit load except that the waves are shifted toward the receiving or load end. The current is zero at 1/8 wavelength from the load and maximum at 1/4 wavelength farther along and then every 1/2 wavelength to the sending end. As the inductive reactance is increased from values less than to greater than the characteristic impedance, the standing waves are shifted toward the receiver or load end as can be seen by comparing Figs. 3-7, 3-9 and 3-11.

When the load is a capacitive reactance, Fig. 2-C, equal to the characteristic impedance, no power is absorbed and standing waves are present in the form given in Fig. 3-10. The line behaves similarly to an open circuit except that the standing waves are all shifted toward the receiving or load end. A current maximum occurs at 1/8 wavelength from the load and every 1/2 wavelength toward the sending end of the line. As the capacitive reactance is reduced from greater than to less than the characteristic impedance, the standing waves are shifted toward the receiver as can be seen by comparing Figs. 3-12, 3-10 and 3-8.

There are many other possible combinations of resistance in series or parallel with either or both inductive and capacitive reactances, Figs. 2-A to 2-F. This discussion is confined to series circuits, since any parallel circuit can be transformed into an equivalent series circuit. Theoretically there are 4 X 4 X 4 + 2 or 66 combinations where the individual components are less than, equal to or greater than the characteristic impedance. A series circuit of resistance, capacitance and inductance behaves like a resistance in series with either inductance or capacitance, depending upon the frequency, except at resonance where it is resistive only. This limits the actual number of cases to 3 X 3 X 3 + 2 or 29. For series loads of resistance and inductance, the wave forms are given in Figs. 3-13 to 3-21. For series loads of resistance and capacitance, the wave forms are given in Figs. 3-22 to 3-30.

If the load is composed of resistance and reactance whose total impedance is equal to the line impedance, the maximum or minimum current or voltage always occurs at exactly 1/8 wavelength from the receiver load, regardless of the resistance to reactance ratio. This can be seen by comparing Figs. 3-31, 3-32 and 3-33 for inductive and resistive loads and Figs. 3-34, 3-35 and 3-36 for capacitive and resistive loads. The maximum-to-minimum ratio of current or voltage approaches unity as the resistance-to-reactance ratio increases.

Fig. 3 - Positions and relative magnitudes of standing waves for various load impedances. The curves show the ratio of current at the point on the line considered to the current in the load.

Reactance variation in a series-resonant circuit - RF Cafe

Fig. 4 - Reactance variation in a series-resonant circuit.

Resistance and reactance variation in an antenna - RF Cafe

Fig. 5 - Resistance and reactance variation in an antenna, looking into a current loop.

When the total load impedance and the resistance component are each greater than the line impedance, an increase in inductive reactance shifts the waves back from the load end, as can be seen by comparing Figs. 3-19, 3-20 and 3-21. Similarly, a decrease in capacitive reactance shifts the waves back from the load end, as can be seen by comparing Figs. 3-30, 3-29 and 3-28. This effect of reactance change upon wave shift is in the opposite direction to the shift obtained with reactance loads only.

With a series inductive reactance and resistance load whose total impedance is greater than the characteristic impedance, the minimum current is always less than 1/8 wavelength from the receiver.

With a series capacitive reactance and resistance load whose total impedance is less than the characteristic impedance, the maximum current is always less than 1/8 wavelength from the receiver.

Some of the curves for current may be applied for the distribution of voltage as well. The line current for the open circuit load is also the line voltage for a short circuit load. The line current for the short circuit load is also the line voltage for an open circuit load. Similarly, Fig. 3-22 represents the voltage for load conditions in Fig. 3-17 and vice versa. Also Fig. 3-26 represents the voltage for load conditions in Fig. 3-13 and vice versa. The voltage and current at some points on the line may rise above the sending and receiving values because of the resonant effect of the transmission line.

An antenna is a series-resonant circuit and may act as a load for the transmission line. In most cases it is inconvenient or impossible to secure a direct match between the line and antenna. It is then necessary to insert some sort of impedance transformer between the antenna and receiver terminals of the line in order to present a load equal to the line impedance. An antenna acts like a pure resistance at resonance, is capacitive and resistive at lower frequencies, and is inductive and resistive at higher frequencies; or, for a given frequency, the antenna is capacitive and resistive if too short and inductive and resistive if too long. The reactance of a series resonant circuit is shown in Fig. 4. The resistance of an antenna changes with frequency or length and is maximum at resonance. The resistance and reactance of an antenna may also be represented as shown in Fig. 5.

Before it is possible to obtain an impedance match and a flat line, the antenna must be tuned to resonance either by adjustment of its length or by inserting a series inductance if too short or a series capacitance if too long. The recognized method is to excite the antenna parasitically and obtain maximum antenna current by tuning. This is laborious and requires accurate measuring equipment. Neither can the exact length of the antenna be calculated for resonance. Many avoid this step by erecting the complete antenna sys-tem and attempting to obtain a flat line by trial and error in antenna tuning and impedance-transformer adjustments. This procedure may result, in rare cases, in obtaining a flat line. It is evident that the number of variables is too numerous to achieve the desired results with a minimum of experiment. At this point a working knowledge of standing waves will enable one to establish the condition of the antenna or the transmission-line load. A scheme is proposed whereby, after determining the relative magnitude and position of the maximum and minimum or loop and node of voltage or current, the antenna condition is indicated by comparison with various curves for different types of loads.

The complete set of curves shown in Fig. 3 covers all possible combinations of loads that may be encountered. By the recognized mathematical methods of differential calculus, the maximum and minimum positions have been calculated by differentiating the line current I_s of equations (1) and (2) with respect to the distance θ, equating to zero and solving for θ. Some of these equations are of second degree and require solution by the quadratic equation method.

The idea in adjustment is to shift the minimum or maximum current to the 1/4 wavelength position (to eliminate the reactive component) and then to reduce the maximum-to-minimum ratio to unity by impedance transformer adjustment. The procedure is to supply sufficient power to the transmission line, with the antenna system in position, to permit measurement of the line current or voltage, starting at the load if possible, and then by measurement at equal small intervals to establish the location of the maximum and minimum voltage or current. In most cases it is preferable to locate the current nodes or minima rather than the voltage, because the change in current per unit length of line is more rapid and easier to detect. One-sixteenth wavelength intervals are sufficiently close to enable one to plot a curve of current or voltage vs. distance to the load. If it is impracticable to start at the load it is permissible to begin at any multiple of a half wavelength from the load, since the standing waves are repeated along the line to the sending end. Radio-frequency waves travel more slowly on transmission lines than in air, so that the length of a wavelength for an open-wire line is usually about 97.5 per cent of that in air.

If maximum or minimum current or voltage occur at points other than at multiples of 1/4 wavelength from the load, the antenna is non-resonant and must first be tuned to resonance by whatever method is desirable. If the maximum current occurs between the load and 1/4 wavelength, the antenna is capacitive or too short and must be lengthened or series inductance added.

If minimum current occurs between the load and 1/4 wavelength, the antenna is inductive or too long and must be shortened or series capacitance added. If maximum or minimum current or voltage occur at 1/4 wavelength from the load, the antenna is resonant but the impedance match is incorrect. The impedance transformer then should be adjusted until the maximum and minimum values are equal or the standing wave ratio is unity.

All the wave forms shown can be encountered during the process of tuning the antenna and matching the line impedance. As the antenna ap-proaches resonance and the impedance match becomes nearly correct, the waves may look like Figs. 3-16 or 3-25. Poor adjustments may yield waves like Figs. 3-21 and 3-30.

It must be emphasized that no adjustment at the sending or transmitter end of the line will change the position of the standing waves. This adjustment will only control the degree of coupling and the amount of power delivered to the line and antenna. A reactive component always appears at the sending end if standing waves are present. It is evidenced by the necessity for resetting the plate tank tuning capacity to obtain minimum plate current when the line is coupled. All adjustments must be made first to the antenna and then to the impedance transformer for the elimination of standing waves. For efficient reception, a proper impedance match must be made at the receiving end. In this case the antenna is at the sending end and the receiver at the output of the line.

With this approach to the standing wave problem, that elusive flat line should be easily realized by all amateurs using untuned transmission lines for their antennas.

Standing Waves on Transmission LinesDecember 1942 QST

Standing Waves on Transmission Lines
December 1942 QST