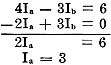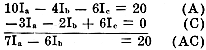|
April 1962 Radio-Electronics
 [Table of Contents] [Table of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Electronics,
published 1930-1988. All copyrights hereby acknowledged.
|

Water manifold - water out = water in: current node.
Not to disrespect
Gustav Kirchhoff's
accomplishments, but his two eponymous laws seem so obvious that you might wonder
why they even need to be stated, much less be named after someone. The equivalent
for the oft-used water in a hose analogy would be as follows: (#1) The volume of
water entering the common port of a manifold is equal to the sum of the water exiting
all the other ports. (#2) In a closed system, the sum of the the pressure drops
(e.g., constricted pipe) and pressure rises (e.g., water pump) is zero. In fairness,
when Mr. Kirchhoff formulated his laws in the middle 19th century not many
people were familiar with electric circuits, and instruments for making certified
measurements with enough precision to validate the claims were not readily available.
This 1962 Radio-Electronics magazine article introduces Kirchhoff's current
law and voltage law. Remembering and applying them does make writing equations for
multi-loop circuits much simpler.
Solve Your Problems with Kirchhoff's Laws
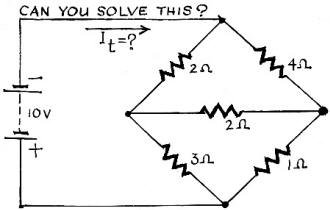
Fig. 1 - This typical bridge circuit looks really hard to calculate
when unbalanced.
It's simple to figure out networks that look hopelessly complicated
By John Collins
Can you solve the bridge problem in Fig. 1? It will probably give you trouble.
Why. Because most radio men are thoroughly familiar with Ohm's law but have little
more than a nodding acquaintance with Kirchhoff's laws. This is unfortunate. Kirchhoff
extended Ohm's theory; and his method makes it easier to analyze complicated circuits
like the bridges, filters and impedance-matching networks so common in radio and
electronics. So the technician who can apply Kirchhoff's method has a leg up over
one whose knowledge stops with Ohm.
Kirchhoff's laws themselves (there are two) are pretty self-evident:
1. The sum of the currents flowing into a junction is equal to the sum of the
currents flowing out of it.
2. In any closed circuit, the sum of the voltage drops is equal to the applied
voltage.
Fig. 2 illustrates these concepts.
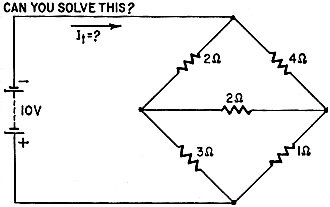
Fig. 2 - Kirchhoff's two laws illustrated.
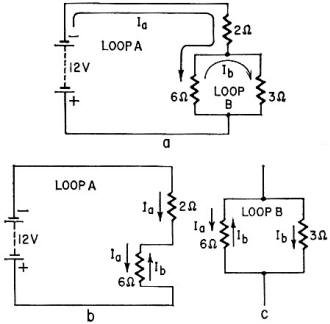
Fig. 3 - How Kirchhoff's laws are applied to a simple series-parallel
circuit.

Fig. 4 - Solution of the Fig. 3 problem.
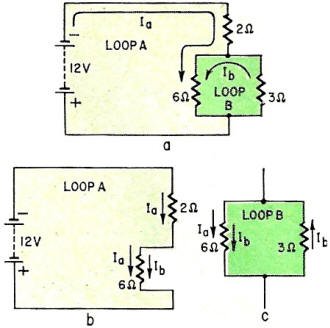
Fig. 5 - Kirchhoff's laws work both ways.
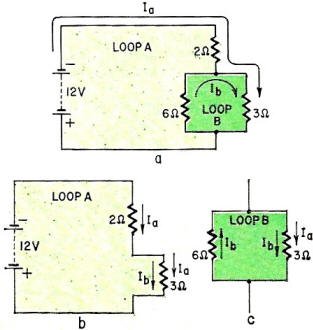
Fig. 6 - In fact, they work three ways.
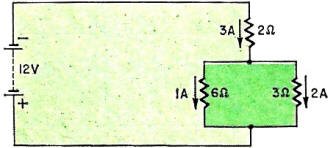
Fig. 7 - Fig. 6's way of getting the answer.
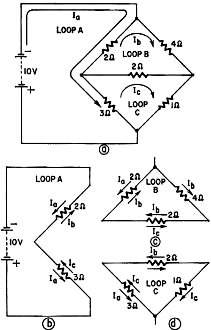
Fig. 8 - Back to the bridge circuit.
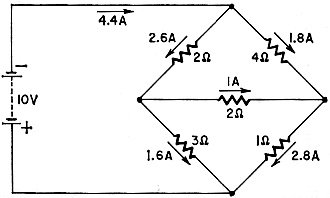
Fig. 9 - Kirchhoff's laws make this as easy to solve as the simpler
circuits.
In applying Kirchhoff's laws to network problems, follow these rules:
1. A separate current is assumed for each closed circuit, or "loop," and is called
its "loop" current. (Since the bridge circuit in Fig. 1 has three closed circuits,
three loop currents are needed for the solution.)
2. In a given loop, the IR drops caused by its loop current are always positive.
3. In a given loop, the IR drops caused by the current from an adjacent loop
may be either positive or negative, depending on whether the direction of flow is
the same or opposite to the direction of the loop current. (Don't worry if you don't
understand this; it will become clear from the examples that follow.)
4. A -voltage source is given a positive sign if its polarity is such that it
aids the loop current - that is, if the loop current flows from negative to positive
in the external circuit. It is negative if it opposes the loop current.
A Practical Example
The above rules are logical consequences of the two laws of Kirchhoff. To demonstrate
how to apply them to practical circuits, we will start with an analysis of the series-parallel
circuit shown in Fig. 3-a. Since there are two loops, we begin by assuming two currents,
In flowing through loop A and Ib through loop B. There is nothing in
the rules about the direction of the assumed currents. We have shown both flowing
in a clockwise direction simply as a matter of choice.
Loop A is redrawn in detail in Fig. 3-b, so that we can concentrate on the factors
in that loop without being distracted by the rest of the circuit. Ia
flows through both the 2-ohm and 6-ohm resistors, producing IR drops of 2Ia
and 6Ia. Since Ia is the "loop" current, both these IR drops
are positive, according to Rule 2 above. However, Ib, from the adjacent
loop, also flows through the 6-ohm resistor. Since its direction is opposite to
L, it causes a negative IR drop, -6Ia. in accordance with Rule 3. The
polarity of the battery is such as to aid in and hence, by Rule 4, it is given a
positive sign.
Putting all these facts together we can now write the equation describing loop
A:
2Ia + 6Ia - 6Ib = 12
(A)
When the two terms involving Ia are added, the equation becomes:
8Ia - 6Ia = 12
(A)
We next examine loop B, as redrawn in Fig. 3-c. You will observe that Ib,
the so-called "loop" current for loop B, flows through both the 6-ohm and the 3-ohm
resistors, creating two positive IR drops, 6Ib and 3Ib, (Rule
2). Since Ia flows in the opposite direction through the 6-ohm resistor,
it produces a negative IR drop, -6Ia, (Rule 3). Finally, since there
is no battery or generator in the circuit, the IR drops are equal to zero.
Expressing these observations as an equation, we write:
-6Ia + 6Ib + 3Ib = 0
(B)
We add the two terms involving Ib, and the equation becomes:
-6Ia + 9Ib = 0
(B)
We now have two equations with two unknown quantities, Ia and Ib.
Any number of values can be found for Ia and Ib that will
satisfy either equation taken by itself. Equation B, for example, can be solved
with any of the following sets of values: Ia = 3, Ib = 2;
Ia = 6, Ib = 4; Ia = 9, Ib = 6; Ia
= 12, Ib = 8; etc. However, only one set of values will satisfy both
Equation A and Equation B. Since both must be considered at the same time to find
this single solution, they are called "simultaneous" equations.
Simultaneous equations are solved by adding or subtracting them in such a way
as to obtain one equation with one unknown. The first step is to modify the equations
by multiplying or dividing them so that a term in one becomes identical with a term
in the other. As long as each of its terms is multiplied or divided by the same
number the equality of the equation is not changed.
To illustrate, we first divide Equation A by 2, and obtain:
4Ia - 3Ib = 6 (A)
Next, we divide Equation B by 3, obtaining:
-2Ia + 3Ib = 0
(B)
Then we add the two equations:
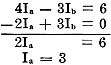
Ib is obtained by substituting the value found for Ia into
either of the original equations. If we substitute 3 for Ia in Equation
B, we obtain:
(-2 x 3) + 3Ib = 0
-6 + 3Ib = 0
3Ib = 6
Ib = 2
To prove the answer, you can substitute 3 for Ia and 2 for Ib
in Equation A. Since they are simultaneous both equations are solved by the same
set of values.
The final solution is obtained by going back to the original problem and filling
in the values we have found for the currents, adding or subtracting them as necessary
where more than one current flows through a branch of the circuit. The result is
shown in Fig. 4. Ia, a current of 3 amperes, flows through the 2-ohm
resistor; Ib, a current of 2 amperes, flows through the 3-ohm resistor,
and 1 ampere, the difference between Ia and Ib, flows through
the 6-ohm resistor.
It's Hard to Go Wrong
In the foregoing example, current flow was in the direction we originally assumed.
In more complicated circuits it is not always easy to tell beforehand which way
the current will flow through a particular branch. Before leaving this example,
therefore, let's see what would happen if we had guessed wrong on the direction
of current flow and had assumed Ib to flow counterclockwise as shown
in Fig. 5.
With the detailed diagram in Fig. 5-b before us, we write the equation for Loop
A:
2Ia + 6Ia + 6Ib = 12 (A)
You will notice that this is identical with the equation we previously found
for loop A, except that the voltage drop caused by Ib now has a positive
instead of a negative sign. This is because Ib
now is assumed to flow in the same direction as Ia through the 6-ohm
resistor, and Rule 3 applies. Adding the two terms involving Ia and dividing
the entire equation by 2, we obtain:
4Ia + 3Ib = 6
(A)
Referring to Fig. 5-c, we write the equation for Loop B:
6Ia + 6Ib + 3Ib = 0
(B)
This equation is the same as in the original example except that the IR drop
caused by Ia in the 6-ohm resistor is now positive, since Ia
is now assumed to flow in the same direction as Ib.
When the terms involving Ib are added and the entire equation is divided
by 3, we obtain:
2Ia + 3Ib = 0
(B)
We then eliminate Ib by subtracting the two equations:
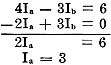
Ib is found next by substituting 3 for Ia in either of
the equations. If we substitute in Equation B, we obtain:
(2 x 3) + 3Ib = 0
6 + 3Ib = 0
3Ib = -6
Ib = -2
A negative sign in the solution means that we have assumed current flow in the
wrong direction, and that it actually flows in the opposite direction. In other
words, our assumption that Ib flows counterclockwise is false, and it
actually flows in a clockwise direction. If we make this correction, we wind up
with the same result as in the original solution, even though we started with a
false assumption.
The fact that answers are always correct, no matter what preliminary assumptions
are made, is one of the more attractive features of the Kirchhoff technique. At
the risk of working this example to death, let's try one more set of assumptions,
as shown in Fig. 6. We again assume that both Ia and Ib flow
in a clockwise direction, but this time we assume that Ia takes the long
route, though the 3-ohm resistor.
The details of loop A are shown in Fig. 6-b. Observing the rules previously stated,
we write the equation for that loop:
2Ia + 3Ia + 3Ib = 12
(A)
5Ia + 3Ib = 12
(A)
Referring to Fig. 6-c, we next write the equation for loop B:
3Ia + 6Ib + 3Ib = 0
(B)
3Ia + 9Ib = 0
(B)
Equation B is then reduced by dividing it by 3, and we obtain:
Ia + 3Ib = 0 (B)
The solution is completed as in the previous examples, by subtracting the two
equations to eliminate Ib and thus find the value of Ia. That
value is then substituted into either of the first equations to obtain the value
of Ib. This procedure yields Ia = 3, Ib = -1.
The negative value means that Ib actually flows counterclockwise.
The result is illustrated in Fig. 7. Ia flows downward through the 2-ohm
resistor, and Ib flows downward through the 6-ohm resistor. In the 3-ohm
resistor, the current is the difference between Ia and Ib,
or a current of 2 amperes in a downward direction. So the final solution is the
same as in Fig. 4, even though we started with a different set of assumptions.
The several other possible combinations will all give the same answer - you can't
go wrong!
Solving a Real Problem
The real benefits of the Kirchhoff method show up in problems that are hard to
handle with Ohm's law. Now that we are familiar with the ground rules, we can tackle
the bridge circuit of Fig. 1. It is redrawn in Fig. 8 to show the three loop currents
needed for the solution and to provide detailed drawings of the individual loops.
We can write the equations easily:
5Ia - 2Ib - 3Ic = 10 (A)
-2Ia + 8Ib - 2Ic = 0
(B)
-3Ia - 2Ib + 6Ic = 0
(C)
No matter how complicated a circuit may be, it is easy to write the equations
describing it. Solving the equations can be harder. When there are only three equations,
it is not hard to combine, say, the first and third to eliminate one unknown, and
then the second and third to eliminate the same unknown. This will leave two equations
with two unknowns, which can then be solved as in the previous examples.
Multiplying the first equation by 2 and adding it to the third equation:
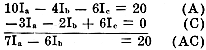
The second equation is then multiplied by 3 and added to the third:

We now multiply Equation AC by 11 and Equation BC by 3 and add them:
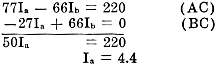
By substituting 4.4 for Ia in either equation AC or BC, we find that
Ib = 1.8. Similarly, by substituting the values found for Ia
and Ib in any of the original equations, we find that Ic =
2.8.
We get the final solution by going back to the circuit diagram and filling in
the values for the currents, adding or subtracting them as necessary. The result
is shown in Fig. 9.
If you want to experiment, you can assume different directions or paths for the
currents. In any case, you should get the same result.
The above examples involve only resistance. Kirchhoff's method works just as
well with impedances in ac circuits. In such problems, the instantaneous current
at some part of the cycle can be used to establish direction. Once you have mastered
the mechanics, you will find Kirchhoff's laws useful in analyzing a variety of circuits
that don't respond to other methods.
Posted June 7, 2024
|