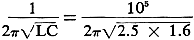|
April 1967 Radio-Electronics
 [Table of Contents] [Table of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Electronics,
published 1930-1988. All copyrights hereby acknowledged.
|
In the March 1967
issue of Radio-Electronics magazine, John Fasal introduced his "Nomorule"
(a nomograph) as a method of simplifying routine electrical design calculations.
In the days prior to smartphones, desktop computers, and electronic calculators,
the choices for such figuring were paper and pencil, slide rule, or nomograph -
or any combination thereof. The nice thing about a nomograph is the visual
presentation of how varying one or more values affects the result. When the
equation at hand is linear, the mental work of extrapolating numbers is not so
hard, but when exponents, logarithms, or trigonometry functions are involved,
things can get tough. Mr. Fasal instructs you on how to generate a custom
nomograph for calculating just about any equation. The only restriction is that
in general only three scales can be in play at a time - akin to a slide rule -
unless other scales happen to fall within the realm of the primary three.
Otherwise, if more than three numbers are involved, equations must be
constructed that combine two or more quantities, with selected ones fixed at a
certain value as a multiplier of the chosen variable. Then, it would be
necessary to construct separate scales for each case. For instance, if you
needed to calculate the voltage across a resistor that was in parallel with a
capacitor and an inductor at various frequencies, you would need to reduce the
equation to just three variables and hold one as fixed. That might be the case
for a resonant circuit across a resistive load, so if the inductor is fixed in
value but the capacitor is adjustable for tuning, an equation would be generated
with the L value as a coefficient and f, C, and R as the nomograph scales. See
Nomorule Part 1
in the March edition.
The Nomorule in Electronic Calculations
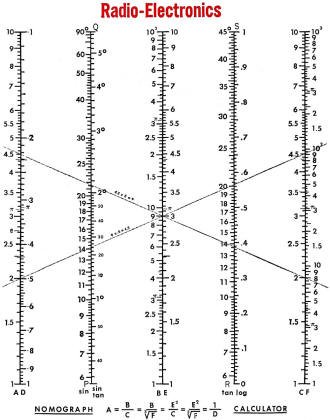
Fig. 1 - Here is the Nomorule again, repeated from last month.
Cut out and mount it on cardboard.
Part 2- More uses for last month's Nomorule: How to multiply and divide
by using logarithms; trig functions and some practical examples
By John H. Fasal*
The basic Nomorule described in Part 1 is repeated here as Fig. 1. We showed
that you can multiply two numbers by aligning a straightedge across one on scale
A and the other on scale C, and reading off the product on scale B. If you have
more than two factors, you must transfer the first product back to either scale
A or scale C, to use it as a factor in the next product.
If any number at B is aligned with 1 on scale C, the line will intersect the
same number at A. This is true because B = AC, and in this case C = 1, so B = A.
Thus we can transfer the number from B to A without changing it.
We can also transfer a number from B to C. Let a line intersect the number at
B with the top index (0.1) at D. At C we will find 0.1 B. The equation used is C
= B/A = BD, and D = 0.1 in this case. We must remember to multiply the transferred
number (A) by 10 to make it equal the original number at B.
Another transfer is possible using 10 on scale C as pole (or pivot point). Align
it with the number at B, and find the answer at A. We are using the equation A =
B/C with C = 10. Therefore A will be 0.1 B and it must be multiplied by 10 to equal
B.
The Nomorule is ideally suited for calculations with trigonometric. functions.
To find the sine of an angle (such as 30°) look for the angle on the "sin" scale
and align it with either point R or point S on the fourth scale (Fig. 2). The answer
is found on B, the center scale. Values of sine for angles between 6° and 90°
lie between 0.1 and 1. For better accuracy, align with point R if the angle is smaller
than 18° (midway up the "sin" scale). Use S for angles larger than 18°.
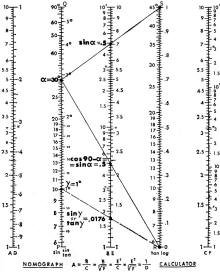
Fig. 2 - Finding sine of any angle, or tangent of a small angle.
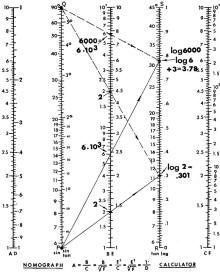
Fig. 4 - How to read the logarithm of a number.
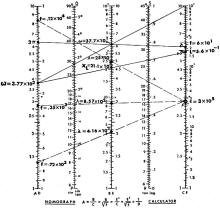
Fig. 6 - Inductive reactance, frequency/wavelength problems.
Sine or tangent values for smaller angles, between 36' and 6°, are based
on the "sin-tan" scale and are calculated in the same way. All readings found on
the B scale, lie between 0.01 and 0.1.
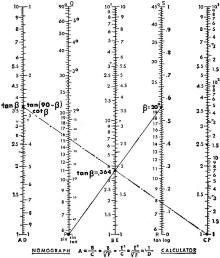
Fig. 3 - Tangents and cotangents are determined like this.
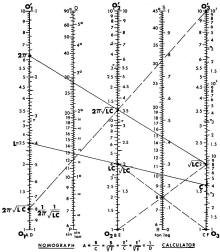
Fig. 5 - Working the resonance formula with the Nomorule.
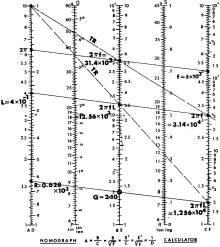
Fig. 7 - Rapid method of calculating Q factor of a coil.
To find the tangent of an angle larger than 6° use the "tan" scale. Align
the given angle (for example, 20° as shown) with either point P or point Q of
the second scale. The answer is tan 20° = 0.364, as shown in Fig. 3. An angle
smaller than 45° has a tangent smaller than 1.
When the angle is greater than 45°, use the equation tan B = cot (90 - B)
= 1/tan (90 - B). For example, tan 70° = cot 20° = 1/tan 20°. To find
tan 70°, determine tan 20°. Transfer the reading from B to the inverse scale
D as shown by the phantom lines of Fig. 3. In other words, we have transferred tan
20° to scale A, then found its reciprocal at D. This indicates 1/ tan 20°
or tan 70°, which is 2.74.
For cotangents of angles smaller than 45°, use the formula cot B = 1/tan
B. Determine tan B on scale B, then transfer reading to inverse scale D. For angles
larger than 45°, use cot B = tan (90 - B). The reading appears on scale B directly.
You can find common logarithms by using the "log" scale with point P or point
Q on the second scale, and the B scale. Align the number (for example, 6) at scale
B with P or Q and read off the logarithm on the "log" scale, as 0.78. To find log
6,000, write it as 6 X 103, and add the corresponding logs. The answer
is 3.78. Log 2 is also shown in Fig. 4: 0.301.
Now how about a couple of practical electronic examples worked out on the Nomorule?
Let's say we want to find the resonant frequency of a circuit having L = 2.5 X 10-1
henries and C = 1.6 x 10-9 farads. The frequency is f = 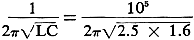
Align 2.5 on scale A with 1.6 on scale C, as in Fig. 5, and find the product
4 on scale B. The square root is read off directly as 2 on scale E. A point on scale
B may be transferred to either scale A or C, as we've said before. But you can't
do it that way from E. Instead, use a "cross alignment" onto scale C, like this:
Connect 2 on scale E with (1) on scale C, intersecting the "tan" scale. Through
this intersection draw a line through 1 on scale E, giving a point on C which is
identical to the original point on E.
The next step is to multiply by 2π on A. This
gives us 12.56 (scale B). Transfer this value to A, using 10 (scale C) as pole.
We are using the relation A = B/C where C is 10. Therefore, the value at A has been
reduced by a factor of 10. It is restored to its correct value by multiplying by
10. Instead of 1.256 (scale A) we actually have 12.56. The last step is to find
the reciprocal of 12.56, which is 0.0795 (scale D). Multiplying by 105
(see formula above), we get the frequency: 7.95 kHz.
Several problems are worked out in Fig. 6. The inductive reactance of a coil
(XL) is given by ωL where ω is 2πf. Let f = 6
x 10, and L = 5.6 x 10-1.
First find 2πf
= 37.7 x 10 as shown. Now transfer this result from B to A, using 10 on C as pole.
We know that this transfer divides the number by 10, so we must multiply by 10 to
compensate. We have, therefore, 3.77 x 102 at A. Now multiply this by
the value of L (at C) and obtain the reactance as 21.1 x 10 at scale B.
Other examples in Fig. 6 show how to convert frequency to wavelength. The formula
is f 300,000/λ, where f is in kHz, λ in meters, and 300,000 is
the velocity of light in km/sec. The Nomorule shows that 416 meters corresponds
to 720 kHz; 857 meters corresponds to 350 kHz and 250 meters to 1.2 MHz.
As a last example, let us calculate the Q at 5 kHz of a coil with 0.4 henry inductance
and 628 ohms resistance, in accordance with the formula Q = 2πfL/R = 2πf(5x10^3)(4x10-1)/628.
Fig. 7 shows how. The first product is read off as 31.4 x 103 on B.
Transfer this result to C by using the top index (0.1) on D as pole. Line TR shows
this. Align this result with 4 x 10-1 at A, and we find 12.56 x 103
at B. Transfer this to C (line TR'), then divide by 0.628 x 103 at D.
The result is 2 x 10.
* Assistant chief engineer, Alarms Engineering, Walter Kidde Co., Belleville,
N.J.
Posted April 8, 2024
|