|
December 1960 Radio-Electronics
 [Table of Contents] [Table of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Electronics,
published 1930-1988. All copyrights hereby acknowledged.
|
As time goes on, more
and more electronic components integrate multiple functions and/or are designed
to accommodate "sloppy" applications. The need to be savvy to the particulars of
transformers is the realm of specialists who manufacture the aforementioned
devices, or those relatively rare few who include transformers into products.
Amateur radio operators (Hams) are likely one of largest groups of practitioners
of analog and RF design who regularly find the need to be bothered with
transformers - mostly for RF impedance matching, not for audio frequencies as
this 1960 Radio-Electronics article addresses. The basic principles are
the same regardless of the frequency of operation, so since the magazine editors
deemed its content useful for its readership consisting of both professionals
and hobbyists, that's good enough reason to include it here on RF Cafe.
Puzzled About Output Transformers?

You can measure the turns ratio and power handling ability of
that idle transformer and put it to use.
By Norman H. Crowhurst
People write to me for advice about output transformers. They want to know which
one to get, or whether a certain transformer can be used in a particular way. They
quote manufacturers' catalog numbers, or even send me sheets torn from catalogs.
But my chances of answering these questions (with any authority) from catalog information
stands only the slightest chance of being better than their own semi-educated guesses.
Then, of course, there's the case of the "unknown" transformer that's been lying
on the shelf. Maybe it could be used for something, but how does one go about finding
out its specifications? Or maybe the specification sheet reads 4,000 ohms center-tapped
to 4, 8 and 16 ohms. Could this be used for an 8,000- (or 2,000-) ohm load?
First, it is practically impossible to tell from published specifications which
is the better of two transformers even for its own job. What complicates matters
here is the fact that no two manufacturers list the same data. Some list rated power,
impedance and frequency response (even if it only says 20-20,000 cycles). Some state
the permissible primary plate current, while others specify the permissible dc unbalance
in the two halves of the primary. Some give dimensions, with or without a case,
while others also include weight. From such diversified information how can anyone
compare products of different manufacturers?
If rated power is given, it probably does not state the lowest frequency at which
this power can be handled. One can only presume, with no guarantee of being correct,
that the lowest figure quoted under frequency response (if this is given) is applicable.
The impedance figure says what it was designed for, but not necessarily for what
mode of operation. A transformer that works well with triodes or triode-strapped
pentodes may not do so well with pentodes, or vice versa. Taps may be provided for
"universal" application, but can these be used for Ultra-Linear? Frequency response
is given, measured in a "standard" test circuit that represents no practical output
arrangement.
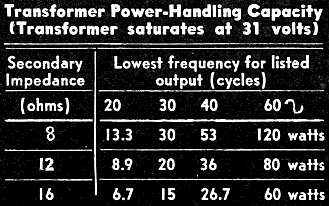
Chart for hypothetical transformer.
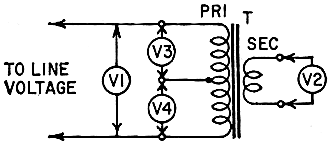
Fig. 1 - Measure all the ac voltages indicated to determine the
turns ratio.
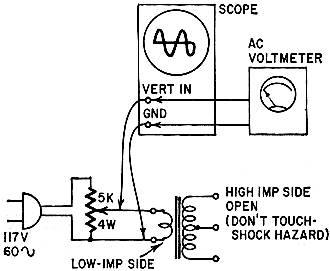
Fig. 2 - An oscilloscope and ac voltmeter are used to determine
the transformer's power handling capacity.
So the more you know about transformers, the more you realize the specifications
usually printed don't really tell you anything, except that the unit is designed
for a specific purpose or as a replacement for some other type. The best answer
is take one and measure it. But what simple measurements can we make to find out
a transformer's capabilities?
Transformer Characteristics
The first thing to find out about an unknown transformer is its ratio. Apply
line voltage to its primary - this should be less than the plate-to-plate voltage
it normally handles, so should not saturate it. Then measure both the primary voltage
and the secondary voltage, with a suitable voltmeter (Fig. 1). Don't bother about
loading it. The ratio between the voltages gives the turns ratio of the transformer,
as close as your voltmeter can measure it.
Suppose the line voltage reads 115 and the secondary voltage 4.6. The overall
ratio is 115/4.6 = 25:1. While you're at it, check that a center tap does divide
the voltage equally. Don't rely, though, on its being exactly half - your voltmeter
may not be that accurate. Rather check that the reading on each half is the same.
Both halves may read 60 volts (or 55) although the total is 115. This is probably
scale error on the meter. By the same token the actual ratio may be anywhere between,
say, 22 to 1 and 27 to 1 for those readings. But loudspeaker impedances aren't so
close that you need to be more critical.
Now you know the turns ratio is 25 to 1. The impedance ratio, or transformation,
is this squared, or 625 to 1. It might be 10,000 to 16 ohms, 5,000 to 8 ohms, or
something like that. Allowing for your voltmeter error, if the ratio is 22 to 1,
the impedance ratio is 484 to 1. If it is 27 to 1, the impedance transforms 729
to 1. On this basis, an 8-ohm load would be transformed to something between 3,900
and 5,800 ohms - that's if it really is 8 ohms and if the transformer losses don't
modify it slightly.
But now you know the ratio, what impedances was it intended for? That you may
never know. More to the point is, what impedances can you use it for? One way to
tackle this is to measure the winding resistances. Then a simple approximate rule
is to multiply the resistance of each winding by the expected power-handling capacity.
Suppose you want to handle 20 watts and the primary resistance measures 300 ohms.
The intended impedance is probably around 6,000 ohms. If the secondary resistance
is 0.75 ohm, the same calculation would give its impedance as 20 x 0.75 = 15 ohms.
But 6,000 to 15 is not 625 to 1. Does this prove your voltmeter readings were off?
More likely the use of convenient wire sizes does not allow equal losses in both
windings. If 15 ohms is correct, then the primary should be 15 x 625 = 9,375 ohms.
The ratio could have been intended for 7,500 to 12 ohms, splitting the difference.
But this is only a rough guide.
The thing to recognize is that the resistance of the windings is your main loss,
except at the low-frequency end. If each winding has a resistance 5% of its working
impedance (or if your working impedance is 20 times the measured resistance of each
winding), the transformer will work at 90% efficiency. If all winding resistances
are then halved in proportion to their respective impedances, the efficiency rises
to 95%.
Power Measurements
To find the actual power-handling capacity, find out where the transformer saturates.
To do this, you will need a 5,000-ohm 4-watt potentiometer as well as a scope. Connect
as in Fig. 2. Now turn the pot up until the waveform goes distorted. Take a voltage
reading at the point where it just departs from a sine wave. Add about 20%, and
this is the voltage-handling capacity at 60 cycles.
Suppose you get 26 volts. Add 20%. This gives about 31 volts. If your secondary
impedance is 16 ohms, the 60-cycle power rating is E2/Z, or (31 x 31)/16,
or approximately 60 watts. If you use it for 8 ohms (in which case your efficiency
will be lower), it will handle (31 x 31)/8, or about 120 watts, at 60 cycles.
Presumably this is a high-fidelity transformer, in which case power is required
to a frequency lower than 60 cycles. Just divide by the square of the ratio between
the frequencies (for example, 60 cycles to 20 cycles or 3 to 1, square is 9). We
have drawn up a little table (Page 33) for the rating of the imaginary transformer
we just measured.
Now we can see the answer to the question about whether a transformer can be
used for other impedances. Used for 10,000 ohms to 16 ohms, the winding resistances
are about 5% each, primary and secondary, so the transformer is about 90% efficient
and will handle 20 watts down to about 35 cycles (interpolating the lower line of
the table). Used for 5,000 ohms to 8 ohms, the efficiency drops to 80%, but it will
handle 20 watts down to about 25 cycles (interpolating second line).
Actually, using different impedances will also affect the high-frequency response.
But to predict this you need to know more about how the transformer is wound - its
winding sectionalizing -as well as the output circuit. However, we can lay down
some ground rules.
Mode of Operation
Starting with the impossible first: pentodes in class B, or semi-class B (class
AB), require very specially designed output transformers - don't try it with strangers!
But pentodes in class A are a fairly safe bet with a simple inexpensive transformer,
using little mixing. You can use feedback without too much likelihood of trouble.
Such a transformer will show equal voltages on primary halves in the ratio test,
but will not have equal resistance in each half.
With triodes, or triode-connected pentodes, you should look for a "better" transformer
- one with more mixing or interleaving of the windings. One where the resistances
of primary halves measure the same, as well as its ratio showing accurate center
tap, is a good one to try.
If you want to try Ultra-Linear operation, my advice is to buy a transformer
designed for it. But you can try a universal job, if you have one around. Use the
outside ends for the plates. The square root of the nominal impedance ratio will
give the percentage tapping for the screens. If the outside ends are nominally 14,000
ohms apart, the 4,000-ohm taps will be √(4,000/14,000) = 0.535, or 53.5%. That's
the nearest you can come to 43%. Higher taps will represent higher percentages.
Another thing about these universal jobs: they are designed as a "replacement"
item. Being a stop-gap measure, their performance is below the standard of items
designed for a specific job. A really high-quality universal transformer can be
made, but it is a laboratory item at a price that would put it out of the replacement
market - or any commercial application.
Catalog Specifications
So much for transformers you can take and measure. But many inquiries are concerned
with possible alternatives to buy, and the only information avail-able is that in
the makers' catalogs.
If weight is quoted, this can give you some clue about low-frequency response,
where the specification omits this information. A transformer with good low-frequency
response and reasonable efficiency for its power rating will run between 2 and 3
watts per pound. So a 20-watt transformer will weigh between 6 and 10 pounds. These
so-called "universal" jobs usually run 10 watts or more per pound, as do most kitchen
radio outputs.
Nominal power is usually quoted, but since it does not say "... watts at ...
cycles," the figure does not mean much. As the tabulation showed, a transformer
that will give 20 watts at 30 cycles can handle 80 watts at 60 cycles. Specification
of frequency response from 20 to 20,000 may or may not mean it will handle its rated
power down to 20 cycles.
Incidentally, the type of output circuit can affect this too. Some circuits can
supply quite a hunk of saturation current in the output transformer before distortion
shows up, others cannot.
A Few Definitions
When you look at a catalog, you read everything pertinent if you really want
to make a critical choice. Knowing this, catalog writers put in all kinds of flowery
descriptions - "scientifically designed," "using the latest engineering principles,"
"applying improved techniques," etc. The implication drawn by the tyro is that a
manufacturer who does any of these things has a better product than one who does
not.
Unfortunately, some who make these claims apparently follow these definitions:
Scientifically Designed: A process consisting of buying a competitor's
sample of a new line, pulling it apart, and making a "Chinese copy."
Latest Engineering Principles: The engineer bought a new slide-rule,
so no longer counts on his thumbs. He has learned to use scales A, B, C and D and
may some day learn what all those other scales are.
Improved Techniques: If the competitor used black paint, we
dip it in shellac. This may make it more durable, but does not affect its performance.
It should not be inferred that all manufacturers use such methods, but I have
been surprised to find how many do! A few years ago I wanted some special filter
transformers made. I had worked out the necessary data; all I needed was someone
to wind them. But this was unorthodox "we don't work that way," "our engineering
department does all our design work."
However, after one company had made them to my data, the rapidity with which
other companies produced Chinese copies was surprising. My experience tells me,
when a representative (styled a "sales engineer") gives me a pitch about his company's
superior engineering facilities, to take it with "a grain of salt." A company that's
really progressive, in transformers as with other things, is one that's first with
really new lines. And don't always believe advertising that says "another first!."
Watch to see who really is first.
Posted June 26, 2024
|












