|
When this article on component
(resistor, capacitor, and inductor) measurement was written, readily available,
inexpensive multimeters were not in existence. For about $20 you can now buy
a brand new handheld DMM that will make very accurate resistance measurements
and reasonably good capacitance measurements at frequencies up to a few MHz,
where lead inductance starts to be significant (test frequency is usually only
a few kHz). Finding an affordable, accurate inductance meter is another story.
Cheap
LCR meters can be purchased on eBay, but don't be surprised if the quality
is not very good. The most accurate measurement method uses a frequency in the
realm of actual operation, and this article presents methods that will allow
you to do just that by using typical bench top instruments.
Component Checking
By N. H. Crowhurst
 A discussion of various ways that circuit
components in radio and audio equipment can be checked without trouble. A discussion of various ways that circuit
components in radio and audio equipment can be checked without trouble.
Sometimes the simpler things one encounters in radio and audio work are apt
to get overlooked. For example, it would seem to be quite an easy matter to
check the inductance of a smoothing choke or the capacitance of an electrolytic
capacitor, with the correct polarizing current or voltage. However, when one
looks around to find a test instrument to make the measurement, it just isn't
readily available, so we are virtually forced into the routine of taking things
for granted.
If we wish to check as to whether a certain component is functioning correctly
or not, the only available method seems to be by substitution, using another
component of the same type. Often this proves to be somewhat unsatisfactory,
because the results can be inconclusive. We really need to know how to check
the various fundamental components used in radio: resistance, inductance, and
capacitance, to varying degrees of accuracy, ac-cording to their purpose.
Resistance Values
The simplest method of resistance checking is by means of a simple ohmmeter,
either an instrument built specifically for this purpose or an ohmmeter range
on a volt-ohm-milliammeter. Accuracy of this method of measuring resistance
rarely exceeds 10% and may not even be as good as this.
Assuming that the accuracy of the moving coil meter used for the instrument
is ±2% and that the resistors used in the instrument are accurate to ±1 %, the
accuracy of the instrument as a perfect comparator between the internal and
external resistances cannot be better than ±1%. And the accuracy of comparison
is only to within ±2% of the full-scale current reading on the scale. If the
scale reading, on a voltage or current scale, is compared with the reading on
the ohms scale, it will be found that an error representing 2% of full scale
in voltage or current reading may amount to an 8% error in resistance value.
This is at the point of maximum accuracy of comparison, between the external
resistance being measured and the internal resistance of the instrument.
Thus it is seen that the best accuracy obtainable using an instrument with
a ±2% movement and ±1 % internal resistance gives a guaranteed accuracy at center
scale reading of 9%. At readings between one-third and 3 times the resistance
value, which is the range one might expect to use before switching to the next
scale, the accuracy can reasonably be expected to stay within 10%. With an instrument
using lower accuracy components than those used for illustration, the accuracy
of the final reading in ohms will be considerably poorer than 10%.
From this it will be evident that an ohmmeter can only be used to make a
rough check as to whether a resistance is within the preferred value range for
which it is color coded - if it is of a ±10% or higher tolerance rating. To
check that the resistance is within ±10% of its rated value, the result is a
little doubtful and it is certainly impossible to rely on an ohmmeter reading
to check to a tolerance of ±5% or closer.
Although the ohmmeter readings cannot be trusted for checking to close tolerances,
it is possible to use an ohmmeter to check for reasonably good matching between
pairs of resistors, if this happens to be the requirement rather than close
precision in actual value.
As an example, in many push-pull amplifiers the resistors responsible for
controlling the gain in the two halves of the push-pull arrangement must be
closely matched to ensure balance. Production values may be specified to 5%
or even closer tolerances, to avoid the necessity of having to select matched
pairs, but the essential feature is that the value of the two corresponding
resistors shall be within a close tolerance of one another. It will not necessarily
matter if both of them are, say, 10% or 15% from their nominal rating, as long
as they are within 5% of each other. This the ohmmeter is reasonably capable
of checking, because it is quite possible to read an ohmmeter scale to within
5%. Since the question as to whether the reading is within 5% of its actual
value is unimportant in this particular application, the significance of the
reading does not matter as much as whether the two resistors which should be
matched give readings within 5% of one another.
For some applications, however, such as calibrated attenuators or instruments
for use in radio it is necessary to check resistor values to closer limits such
as 5%, 2%, or even 1%, as the case may require. In these circumstances it is
important that the value shall really be within the specified percentage of
its rated value. The only method of making a measurement that is satisfactory
for this purpose is to use a Wheatstone type bridge, using calibrated elements
whose accuracy is better than the required component accuracy.
For most radio purposes the Leeds & Northrup bridge used for telephone
line work is quite accurate enough. In using a bridge there are two things that
control the accuracy of the reading obtained: (1) the accuracy of the resistance
elements of the bridge itself, and careful attention to see, that contact resistance
does not contribute an appreciable fraction under any circumstances; and (2)
the sensitivity of the null detector.
This second cause of inaccurate results can be checked by unbalancing the
bridge by a known percentage to see that an adequate off-balance reading is
obtained. Suppose, for example, the value required is 120,000 ohms, ±5%. Having
balanced the bridge and obtained a null at, say, 120,000 ohms, the resistance
in the calibrated arm should be altered by 5%, which represents a change of
6000 ohms.
If clicking in 6000 ohms additional in the calibrated arm shows appreciable
deflection, then the reading may be regarded as accurate; but if the addition
of 6000 ohms does not produce noticeable deflection from balance on the null
detector, the result is not reliable. To improve its reliability one can either
use a larger battery voltage or source of supply to the bridge, or else get
a more sensitive null indicator.
Before leaving this discussion of resistance values it should perhaps be
emphasized that it is not wise to put absolute trust in the color coding on
a resistor. Occasionally even the best resistor will be found incorrectly color
coded. If the error happens to be in the third color of the code, then the discrepancy
in resistance value will be a matter of shifting the decimal point which can
be quite serious. Also with some sets of coding colors the difference between
some of the colors is somewhat difficult to determine, especially after the
component has aged. For example, orange and brown can get to look quite alike.
Usually the first and second colors in the code can be identified by the
combination used, from the recognized preferred value range. If the first color
is blue, representing 6, the second color will most likely be either red, representing
2, or gray, representing 8, because 62 and 68 are the preferred values in the
60 to 70 range. But there is no such ready clue as to the likely color of the
third band: it could just as easily be brown or orange. Thus a resistor in which
this color looks at all doubtful could be either 620 ohms or 62,000 ohms, which
is a considerable difference!
This is where an ohmmeter check can easily determine which of the two values
is correct.
Inductance

Fig. 1 - Bridge configurations for measuring inductance.
(A) the "Hay" bridge. (B) the "Maxwell" bridge. Relative advantages of each
type are discussed in the article.

Fig. 2 - Modification of the "Hay" bridge to enable
it to measure inductance with polarizing current flowing. Care is necessary
not to exceed the dissipation rating of the various bridge elements. See text.
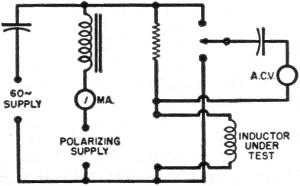
Fig. 3 - A simple inductance checker circuit for determining
inductance with the polarizing current flowing in the component.
Turning now to various kinds of inductance: the measurement of components
not intended for the passage of d.c. and without iron cores is a fairly simple
matter, with the aid of a conventional inductance bridge. Using such a bridge,
employing either the Hay or Maxwell configuration (see Fig. 1), the inductance
can be measured at a frequency suitable for the purpose, with a method quite
similar to the operation of a bridge for measuring resistance.
The principal difference is that two kinds of adjustment are usually necessary
to achieve null, because of the necessity for balancing the bridge in both amplitude
and phase. This enables the bridge to give a reading of both inductance value
and "Q" or loss factor. Bridges of this type are clearly marked to indicate
the correct setting of the controls for making each kind of measurement.
There is usually no difficulty in achieving a null with the air-core type
of coil, but if the inductance employs any kind of core, the null may not be
quite as definitive, because of the distortion of the injected test signal caused
by the core. Also, if the generator signal itself has any appreciable harmonic
content, a Hay bridge will never give a balance at both fundamental and harmonics
at the same setting. On the other hand, with an inductance where the only loss
is due to its resistance, such as occurs in an air-core coil, the Maxwell bridge
will give a fairly satisfactory balance for both fundamental and the lower harmonic
frequencies at the same setting.
When measuring an inductor that employs any kind of core to increase the
permeability, the magnetizing current is liable to distort so the inductor itself
will generate some harmonics not present in the input from the generator. When
the bridge is balanced to the fundamental generator input, there will be a residual
harmonic present at the null point, generated by the inductor itself.
This is a good reason for using ear-phones if the generator frequency is
in the audio range. Otherwise an oscilloscope with amplifier may be used as
a null detector. It is then possible, listening to the tone or looking at the
trace, to determine when the fundamental is balanced and the residue consists
of harmonics.
But the conventional type of bridge is only suitable for measuring inductances
where there is no polarizing current. The usual variety of smoothing filter
choke has to provide a specified inductance when polarizing current is flowing
and the inductance in the absence of such polarizing current will be considerably
higher than the rated inductance of the choke with polarizing current. Unfortunately
there is no simple fixed relationship between these two values.
If the choke has been designed to provide its maximum inductance at the polarizing
current for which it is designed, the air gap will be adjusted so that, at this
value of polarizing current, either reduction or increase of the air gap would
result in a reduction of inductance value. However, in the absence of polarizing
current, increasing the air gap will always reduce inductance value, while reducing
the air gap will always increase inductance value.
From this simple fact it is evident that measuring an inductance with no
polarizing current flowing is no criterion of its performance with polarizing
current. It can, of course, provide a check that the inductance is not completely
missing, due to short-circuited turns, in which case the inductance might not
even be adequate without polarizing current flowing. But the fact that the inductance
may measure twice its required value with polarizing current is no evidence
that the choke will give its rated value with polarizing current.
Fortunately, with filter chokes of this nature close tolerances are not too
important. Usually a compliance with a minimum inductance value will suffice.
It is sometimes possible to use a modified Hay bridge, as shown at Fig. 2,
to inject a polarizing current so as to measure the inductance with the polarizing
current flowing. But this can be a dangerous procedure, because the polarizing
current may exceed the wattage rating of some of the internal components of
the bridge and cause permanent injury to it. It is, therefore, better to devise
a simple checking arrangement, as shown schematically in Fig. 3.
This does not employ a bridge method, but checks the inductance by injecting
a known frequency and comparing the a.c. voltage developed across the inductor
with that across the resistor in series with it. The relation between the a.c.
components of voltage developed will enable the approximate inductance value
to be calculated. This does not take into account the effect of the inductor
distorting the waveform of the a.c. signal component, which invariably occurs
in this type of inductor and is, in fact, another reason why any attempt to
produce a precise figure of inductance will be somewhat meaningless. A rough
check of this nature is quite adequate for the purpose.
If 60 cycles is the supply frequency for the a.c. component, dividing the
calculated impedance of the inductor by 377 will give the inductance value.
For example, suppose the series resistor used is 100 ohms (carefully checked
in value), and the a.c. voltages measured across the resistor and inductor are
2 and 30 volts, respectively: then the impedance of the inductor at 60 cycles
is 1500 ohms, representing approximately 4 henrys.
Capacitance

Fig. 4 - The "Drysdale" bridge which is used for measuring
capacitance. Refer to text.

Fig. 5 - A simple bridge for capacitor checking that
forms the basis of a number of commercial units on the market. The null detector
is usually a "magic eye" tube.

Fig. 6 - Modification of a "Drysdale" bridge to permit
the measurement of electrolytic capacitors with polarizing voltage applied.

Fig. 7 - Modification of the simple bridge of Fig.
5 to enable polarizing voltage to be applied to the electrolytic capacitors.
For measuring all except electrolytic capacitors there are two methods, which
correspond in relative accuracy with the ohmmeter and bridge methods used for
measuring resistance.
The Drysdale bridge (see Fig. 4) is a modified Wheatstone bridge, in
which resistance arms are used in the ratio positions, while a calibrated decade
capacitor is substituted for the calibrated resistance in the variable standard
arm. This type of instrument can give capacitance results comparable to those
obtained with the Wheatstone or Leeds & Northrup bridge for resistance,
but its use involves careful adjustment of a number of controls until a null
is achieved.
The alternative method of capacitance measurement also uses a bridge, but
one in which the null is much more quickly achieved. In this bridge (see Fig. 5)
a standard capacitor is used in one arm, the unknown capacitor in another arm,
and a single potentiometer-type resistance for the other two arms. This resistance
is calibrated on the basis of the ratio between the unknown and standard capacitors
necessary to achieve null.
With this type of bridge the unknown capacitor is connected across the terminals
of the bridge and the one dial turned until null is indicated. The capacitance
value is then read off the dial. The accuracy of this type of instrument is
usually comparable to that of an ohmmeter, depending upon the accuracy with
which the potentiometer type resistance has been calibrated.
Neither of these methods is really satisfactory for the measurement of electrolytics.
This can better be understood by discussing a little further the behavior of
electrolytic capacitors under different conditions.
In the first place, electrolytic capacitors freshly formed ready for use,
have a dielectric film on the active plate of the correct thickness for the
working voltage. Under this condition the capacitor should have its rated capacitance.
But if the capacitor is operated consistently at a lower polarizing voltage,
the thickness of the formed film will gradually deteriorate with the result
that the effective capacitance will increase somewhat. This is not necessarily
detrimental to the performance of the capacitor, provided it is not subsequently
required for service at its nominal working voltage.
In much the same way electrolytic capacitors kept in storage also show a
deterioration in the dielectric film resulting in an increase in effective capacitance.
This means if a six-month-old capacitor is taken from the shelf and measured
on a regular capacitance bridge, without applying the necessary polarizing,
it will probably show a value considerably in excess of its nominal value. However,
it will not be satisfactory for operation until the electrolytic film has been
formed up to the requisite thickness for its working voltage.
This will have to be done with the aid of a limiting resistor connected in
series with the capacitor to limit the polarizing current while the film is
forming. Only when the film has formed up so the voltage appearing across the
capacitor is at its working value without excessive leakage current can its
capacitance be measured to give a reliable indication of its operating condition.
Also, if the capacitor is to be installed in a piece of equipment for operation
at its nominal working voltage, it is vital that this reforming of the capacitor
be performed before installation, so the capacitor does not take an abnormally
high leakage current when the power is switched on and possibly destroy itself
before it has had a chance to become correctly reformed.
The correct measurement of electrolytic capacitors with polarizing voltage
applied can be undertaken with either type of bridge, modified to a certain
extent, as shown in the schematics of Figs. 6 and 7. If the actual capacitance
value of an electrolytic capacitor is not vital, which often is the case, then
all that is necessary in installing a new one is to ensure that it is correctly
formed to its working voltage before connecting it in. This may be done with
the aid of the circuit shown in Fig. 8, which consists of a high resistance
feeding the capacitor with a voltmeter across it to indicate when working voltage
has been reached. The resistor limits the leakage current through the capacitor
to well within the maximum leakage current allowed, and when the capacitor has
reached its nominal charged voltage, it can then be removed from the charging
arrangement. Then, after discharging the capacitor for the sake of safety, the
capacitor is ready for installation in its intended circuit. Discharge should
preferably be accomplished through a fairly large resistor. The common practice
of short-circuiting a fully charged capacitor results in a very high discharge
current that may damage the capacitor.
Sometimes a capacitor which has been in stock a long time will deteriorate
in the quantity of electrolyte present, so the capacitance will fall low in
value, even after it has been adequately reformed.

Fig. 8 - Details for constructing a simple jig for
forming electrolytic capacitors up to their working voltage.
If it is not convenient to build a capacitance measuring arrangement incorporating
the polarizing supply, a fairly legitimate result can usually be achieved by
ensuring that the capacitor is correctly formed using the polarizing jig of
Fig. 8, then discharging the capacitor and finally measuring it immediately
with the aid of one of the conventional capacitance bridges without polarizing
voltage.
If the electrolytic capacitor is reasonably stable, a null will be obtained
which will not vary at a perceptible rate. If the capacitor is not sufficiently
stable to be reliable in use, the null may be observed to vary perceptibly while
the measurement is being taken. If the capacitance varies at a rate that can
be noticed while making the measurement, then the capacitor should be discarded
as insufficiently stable for reliable operation.
The foregoing discussion has covered the more common measurements necessary
on resistance, inductance, and capacitance. Sometimes much more precise methods
of measurement are necessary, especially where the equipment is for some kind
of standard operation such as a precision oscillator. In this kind of application
it is often necessary to make measurements, not only as to the precise value
at room or ambient temperature, but to determine the effect of temperature on
the component. To make such measurements, only precision bridge apparatus is
satisfactory, and the component should be measured under carefully controlled
conditions of temperature and the measurements repeated at different temperatures,
to discover what temperature coefficient the component possesses. Fig. 8.
Details for constructing a simple jig for forming electrolytic capacitors up
to their working voltage. See article.
Posted November 12, 2019
(updated from original post on 7/8/2013)
|


















