Derivation of Phase Angle Error Due to VSWR Mismatch
by Haris Tabakovic

Try finding the equation for phase angle error due to VSWR mismatch, and you will likely fail. Extensive keyword searches for related terms will turn up websites that present the formula for amplitude error due to VSWR mismatch, but not for phase angle error due to VSWR mismatch. If you are fortunate enough to find the equation, you almost certainly will not be given the derivation.

The actual equation, εθ_max = |Γ₁ | • |Γ₂|, is so simple that it seems unbelievable, but here its validity is demonstrated.

Well, the search is over thanks to Haris Tabakovic, who was kind enough to provide this excellent derivation for the benefit of RF Cafe visitors.

V₁ = V_i • T₁

V₂ = V_i • T₁ • e^-jβl

V_o = V_i • T₁ • T₂• e^-jβl

V_o is expected output signal.

At the same time, the reflected signal is being bounced around on the connecting transmission line. First order reflections are going to be dominant, and higher order reflections are not taken into account. Note that the transmission line is assumed to be lossless.

Then we can express reflected signal at V₂ as:

V_2r = V_i • T₁ • e^-jβl • Γ₂

This signal travels back and reflects again at V₁ :

V_1r = V_2r • e^-jβl • Γ_{1 =} V_i • T₁ • e^-jβl • Γ₂ • e^-jβl • Γ₁

Finally, this error signal V_oe is transmitted and superimposed on expected output signal, causing phase and amplitude error:

V_oe = V_1r • e^-jβl • T₂ = V_i • T₁• e^-jβl • Γ₂ • e^-jβl • Γ₁ • e^-jβl • T₂

V_oe = V_i • T₁ • T₂• Γ₁ • Γ₂ • e^-j3βl

We can represent these signals in complex plane as:

|Vo| = |Vi| • |T1| • |T2| |Voe| = |Vi| • |T1| • |T2| • |Γ1| • |Γ2|

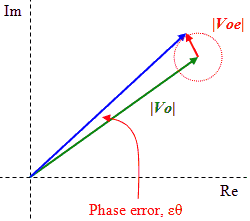It follows that we can write the worst-case phase error εθ_max as:

Since εθ_max will be a very small angle, can say that:

tg(εθ_max) ≈ εθ_max

Finally, we can write the worst-case phase error (in radians) due to reflections at the source and at the load as:

εθ_max = |Γ₁| • |Γ₂|

Here is an online VSWR mismatch calculator.

Posted June 6, 2023
(updated from original post on 2/15/2009)