An article written by Tom Lecklider in the October 2005 edition of
Evaluation
Engineering titled "
The World of the Near Field"* presented formulas for three regions
of the near field that relate the largest physical dimension of the radiator to
the operational wavelength. A great chart shows the transition area between near
field and far field. There tends to be a lot of opinions (rules of thumb) about
where the transition regions exist.
There was also an article in the February 2001 edition of Conformity
entitled, "Near and Far Fields - From Statics to Radiation" that did a good job
of addressing the near field vs. far field issue.
The calculator originally on this page has been removed because of compatibility
issues with outdated Microsoft OWC components. A Near-Field/Far-Field Calculator
is included in
Espresso Engineering Workbook™ for FREE.
Per Mr. Lecklider, the field boundaries are as follows:
- For electrically small antennas
(compared to wavelength), the Reactive Near
Field Boundary is given by
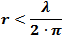 .
.
- For electrically large antennas,
the Reactive Near Field Boundary is better described
by
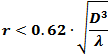 .
.
- For electrically large antennas,
the Radiating Near Field Boundary is given by
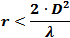 .
.
|
AM = 530-1710 kHz
FM = 88-108 MHz
ISM = 902-928 MHz
PCS = 1850-1990 MHz
RFID = 13.56 MHz
|
GPS = 1575.42 MHz
802.11b/g = 2.40-2.48 MHz
802.11a = 5.15-5.82 MHz
DBS = 12.8-14.5 MHz
|
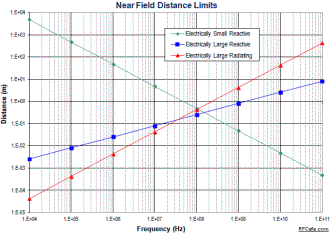
This chart plots the near field/far field transition distance for a range of
frequencies.
* Electronics Design republished "The
World of the Near Field" after the
EvaluationEngineering.com website disappeared.
The following page was retrieved from the WayBack Machine at
archive.org. I have tried to contact the current owners of the
former Conformity magazine for either a page on their website to link to, or for
permission to post it on RF Cafe, but have not been able to get a response.
Since it is such an excellent primer on the near field vs. far field topic, I am
posting it here until such time as I am either directed to remove it, or, preferably,
provided a hyperlink on their website.
Near and Far
Fields - From Statics to Radiation
February 2001
Conformity
By Isidor Straus and Curtis-Straus LLC
Since we've got a focus article on shielding in this issue, it seems timely to
review the relationship between source configuration, operating frequency, measurement
distance, and wave impedance. Wave impedance is the ratio of the electric field
magnitude, E, to that of the magnetic field magnitude,
H. It characterizes an electromagnetic field with the same units - ohms
-- as the circuit concept impedance does. The ratio of E, which
is in volts per meter, to H, in Amperes per meter, is simply ohms.
In shielding, this ratio plays an important part in the mechanisms of reflection
and absorption, which play a key part in EMI/EMC control.
In this article, we'll show that the wave impedance in free space is determined
by two things:
- The physical details of the radiating source-whether it is open ended (dipolar),
or closed (current loop),
- and perspective-is the measurement taken from a nearby or distant point, that
is, in the near or far field.
Statics First
For our purposes, circuits that cause fields can be sorted into four basic classes:
1. Electrostatic
2. Magnetostatic
3. Electric, time-variant
4. Magnetic, time-variant
The electrostatic class is simply a fixed distribution of charges. Since the
charges do not move, no current flows. A simple familiar (but useful) case is the
charge dipole, where two equal and opposite charges are spaced some distance apart.
Another would be one or wires held at some fixed voltage or voltages. Under these
conditions, there is an electric field which does not vary with time (E
is constant in time). There is no magnetic field (H is zero). The
concept of wave impedance isn't useful in electrostatics because the ratio of
E to H is infinite.
For a charge dipole, the electric field falls away as the cube of the distance.
The inverse cube law is derived from the near cancellation of fields by the opposite
charges. Each charge has an field which falls off as 1/r2, but because
the charges are of opposite signs, the resulting field falls off more rapidly.
Magnetostatic circuits consist of DC current loops. This is the dual to the electrostatic
case. There is a constant magnetic field H which is time invariant
and falls off with the cube of distance, but no electric field (E
is zero). Hence wave impedance isn't of interest here either - it would be zero.
In fact, for both the electrostatic and magnetostatic cases, wave impedance is meaningless,
because there are no waves-nothing is changing, and field information doesn't propagate
magnetostatic cases, wave impedance is meaningless, because there are no waves-nothing
is changing, and field information doesn't propagate.
Varying the charges and currents
Once we have variation in either charge or current distribution, we will have
changing fields. Maxwell's equations tell us that we can't change an electric field
at any point without there being a corresponding change in the magnetic field, and
that information on the change (i. e., changes in the fields at more distant points)
will propagate away at the speed of light in the surrounding medium.
We can reconcile the concept of wave propagation with those of electro- and magnetostatics
by looking at the way electric and magnetic time-variant circuits behave by looking
at the way electric and magnetic time-variant circuits behave.
The third class of circuit mentioned above is a time-variant electric circuit.
We could start by thinking of a slowly varying electrostatic circuit. Consider these
more or less equivalent cases:
1. a charge dipole where the charges vary sinusoidally
2. a current element where current flows back and forth sinusoidally along a
line (charges would build up and reverse at the ends, so this is equivalent to the
previous example)
3. any assemblage of open-ended wires driven by voltage sources, including dipole
and whip antennas, as well as low speed leads exiting circuit boards driven by common
mode voltages
A short sinusoidally varying current element is known as a "Hertzian dipole."
"Short" means small in comparison with a wavelength at the drive frequency, so the
current is uniform over the wire at any instant. To understand the relation ship
between the charge dipole and the time-varying current element, think of the charges
as varying with time. If each charge at the end of the dipole has the value
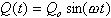 , then a current equal
to the rate of change of the charge,
, then a current equal
to the rate of change of the charge,
 will flow.
will flow.
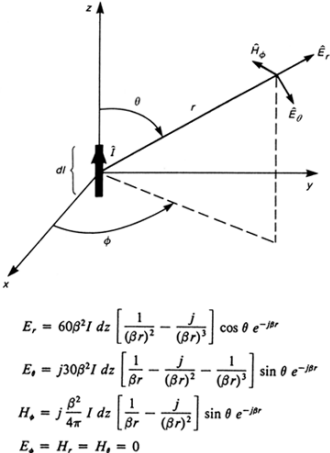
Figure 1 - A sinusoidal current element produces large electric
fields in the near field because of the 1/r3 term.
Figure 2 - A sinusoidal current loop produces large magnetic
fields in the near field. In the formulae, the term "dm" stands for the magnetic
moment, given by the product of current and loop area.

Figure 3: The wave impedance measures the relative strength of
electric and magnetic fields. It is a function of source structure.
A mathematically exact description of the electric and magnetic fields generated
by the infinitesimal Hertzian dipole is shown in Fig. 1.
Note the following:
1. Both electric and magnetic fields are present.
2. The electric field contains components which vary as 1/(ßr)3, 1/(ßr)2, and
1/ ßr, where ß = (2π/λ,
and the wavelength λ
= (c/f), where c is the velocity of light and f is the frequency.
3. The magnetic field contains components which vary as 1/(ßr)2, and
1/ ßr.
4. The quantity (ßr) can therefore be rewritten as
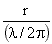 .
.
It is unity at a distance of ro =
λ/2π.
For r<< ro, 1/(ßr) is the dominant term. This is what we call the
near field, and is electric. For r >> ro, 1/ ßr is the dominant
term. This is the far field. Note that in the far field, E and H are related by
the characteristic impedance of the medium (120π or 377 ohms for
a vacuum). In the vicinity of ro, there is a transition region where
all terms are of the same order of magnitude.
What does this tell us? For one thing, the terms "slow", "fast", "near" and "far"
are all relative. A "slowly" varying Hertzian dipole is one that we are "near" to
in the sense of being much closer than
λ/2π
when we measure it. Since wavelength and frequency are inversely related, low frequencies
have long wavelengths and vice-versa.
The dual to the Hertzian dipole is our fourth case, a sinusoidally excited current
loop. A current loop is characterized by its "moment," which is the product of the
current it carries times its amplitude. Looking at figure 2, we see that the electric
and magnetic fields for a sinusoidally driven infinitesimal current loop mirror
those for the Hertzian dipole. Here, the near field magnetic field exhibits 1/r3
behavior, while the near-field electric strength falls off as 1/r2. In
the far field, both E and H exhibit 1/r behavior. Their ratio, which is the wave
impedance, is the characteristic impedance of the surrounding medium, just as it
is for the Hertzian dipole.
In the far field, both sources "look" the same. That is, given measuring equipment-antennas
and a field strength meter-we would have no way of knowing whether the electric
and magnetic fields we measured were created by a dipolar or current loop source.
This is the situation for measurements taken above 30 MHz for FCC and CISPR measurements.
The dividing line between near and far field at 30 MHz,
λ/2π
, is only 1.6 meters. Therefore, we expect 1/r behavior, or inverse scaling, for
high frequency measurements. Deviations from true 1/r behavior usually have to do
with the fact that the equipment under test is not a point source, and due to site
and ground plane reflections.
At low frequencies, however, the situation is quite different. Consider a magnetic
source-a driven loop - operating at 60 kHz. This source could be the horizontal
drive of a CRT monitor, or a switching power supply, or the field coil in a magnetic
security system. The dividing line between near and far field at this frequency
would be 800 meters. Any practical measurements would be taken in the near field
at a much closer distance of the magnetic fields with a loop antenna. It would be
easy to demonstrate inverse cube law dependence of the field strength with distance.
Electric field strengths would be relatively low in the near field for a loop-like
structure. Low E and high H mean low wave impedance (see figure 3).
Conversely, a dipolar source measured in the near field would exhibit strong
electric fields and weak magnetic fields. High E and low H mean high wave impedance.
In both cases, as the distance increases to the far field, the wave impedance approaches
that of free space.
The FCC and CISPR ITE standards mandate the use of magnetic field antennas (shielded
loop) below 30 MHz and linearly polarized electric field antennas (dipoles, biconicals,
log periodics) at higher frequencies. This essentially assumes that only magnetic
fields from loop-like sources are of interest at the lower frequencies (say below
5 to 10 MHz). This is by no means a universal regulatory policy. Both military (MIL-STD-461/2)
and Bellcore (GR-1089) include the requirement to also measure low frequencies with
an active 1 meter long whip antenna, which is electric field sensitive.
return to Conformity
return to This Article
Copyright and Disclaimer ©2001 Conformity®
Related Pages on RF Cafe
-
Antenna Patterns
-
Antennas - Hardware & Controls
-
Antennas - Manufacturers & Services
-
Test Equipment & Calibration - Antenna Measurement
-
Antenna Introduction / Basics
-
Antenna
Radiation Patterns
-
Antenna
Near Field
- Near-Field
/ Far-Field Transition Distance
-
Intro
to Wave Propagation, Transmission Lines, Antennas
-
Antenna, Electromagnetics & X-mission
Line Simulators
-
Satellite Communications - Antennas
-
Short Wire Antennas
Posted February 5, 2013







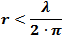 .
.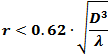 .
.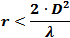 .
.
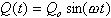 , then a current equal
to the rate of change of the charge,
, then a current equal
to the rate of change of the charge,
 will flow.
will flow.


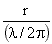 .
.