|
June 1932 Radio-Craft
 [Table
of Contents] [Table
of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Craft,
published 1929 - 1953. All copyrights are hereby acknowledged.
|
It seems most of the articles we
see on the subject of attenuator pads are based on signal reduction in terms of
decibels for units of power. Although it is a simple matter to convert power decibels
to voltage decibels, it would be more convenient if you are working with voltage
to have formulas and tables of values based on voltage ratios. This article does
just that.
As a reminder, the decibel representation of a ratio is always 10 * log10 (x).
If you have a voltage ratio of V1/V2 = 0.5, then
10 * log10 (0.5) = -3.01 dB. If you have
a power ratio of P1/P2 = 0.5, then 10 * log10 (0.5) = -3.01 dB.
Does that mean that -3.01 dB of voltage attenuation is the same as 3.01 dB
of power attenuation? Confusingly, no.
Let's say for the sake of simplicity that you have 1 V across a 1 Ω
resistor, yielding a power dissipation of P = V2/R = 12/1 = 1 W.
Now, reduce the voltage to 0.5 V
and the power dissipation is 0.52/1 = 0.25 W. The ratio
of the voltage change is 1:2 but the ratio of power change is 1:4. In decibels of
voltage that represents 10 * log10 (0.5) = -3.01 dB,
but in decibels of power it represents 10 * log10 (0.25) = -6.02 dB.
A multiplication factor of 2 therefore exists between voltage ratio and power ratio
when applied to the same system.
Now, let's work it in the opposite direction. For the sake of simplicity again,
you have 1 W being dissipated by a 1 Ω resistor, yielding a voltage
across it of V = sqrt(P*R) = sqrt(1*1) = 1 V.
Now, reduce the power to 0.5 W and
the voltage across the resistor is sqrt(0.5*1) = 0.7071 V. The ratio of the
power change is 1:2 but the ratio of voltage change is1:0.7071. In decibels of power
that represents 10 * log10 (0.5) = -3.010 dB,
but in decibels of voltage it represents 10 * log10 (0.7071) = -1.505 dB.
Once again as you would expect, a multiplication factor of 2 exists between voltage
ratio and power ratio when applied to the same system.
The Theory and Construction of Attenuators, Line Filters and Matching
Transformers (Part I)
The Theory and Construction of Attenuators, Line Filters and Matching
Transformers (Part II)
The Theory and Construction of Attenuators and Line Filters (Part
III)
The Theory and Construction of Attenuators, Line Filters and Matching Transformers
(Part II)
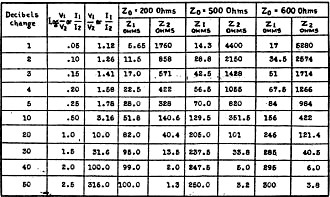
Table 3 - Attenuator Impedance Values
In this second of a series of articles, the author will discuss additional design
considerations of attenuators, illustrating them with numerical examples.
By Hy Levy, B.S.
Last month, some of the more pertinent problems of transmission lines (with
special reference to "pads" or "attenuators") were outlined. In this issue, we will
continue with a discussion of actual design considerations.
The two extreme conditions that a transmission line could be subjected to are
an open-circuit and a short-circuit condition; in which cases, the greatest reflection
of energy will take place, and abnormal voltages and currents will be set up from
small impulses originally sent into the line. This is the same as saying that infinite
impedance terminates the line on open circuit, and zero impedance terminates the
line on short circuit. These two conditions are very rarely encountered in practice,
unless the line should accidently become open or shorted at the far end.
Assume a transmission line in which the line conductors have negligible attenuation
(zero losses) and in which the generator or source impedance is of known value.
Then, if a terminating impedance is inserted at the far end of the line, and starting
from the open-circuit condition of infinite impedance, this terminating impedance
is gradually made smaller and smaller, the reflected energy will also become smaller,
and as the terminating impedance approaches the value of the source impedance, the
reflected energy rapidly decreases. At the point where the value of the terminating
impedance exactly equals the source impedance, the reflected energy will be zero
(no reflection losses), and maximum energy will be obtained at the load.
Likewise, starting with the short-circuit condition of zero terminating impedance,
and increasing the load impedance, the reflected energy becomes smaller, so that
when the point is reached where both the terminating and the source impedances are
exactly equal, the reflected energy will be zero (no reflection losses), and maximum
energy will again be fed to the load.
When the terminating or load impedance exactly equals the source impedance, the
line has the same characteristics as a line of infinite length. If a line of infinite
length could be constructed, any energy sent into this line would never be reflected
back to the source. By inserting at the far end of a transmission line a load or
terminating impedance equal to the source or generator impedance, the characteristics
of a line of infinite length are immediately obtained (assuming zero losses in the
circuit) and consequently no reflection losses are set up in such a circuit.
This entire discussion on reflection losses can be summed up by stating that
the cause of these losses is improper impedance matching, and it is for this reason
that the subject of proper impedance matching is so strongly stressed and observed
in voice transmission circuits. In order to avoid reflection losses, care must be
taken to see that, at any point in a transmission line where an impedance is to
be inserted, this terminating or load impedance is made equal to the impedance working
into it. Reflection losses, as previously stated, give rise to abnormal voltages
and currents; harmonics are set up, and the wave form of the impressed original
signals are distorted, with the result that straight-line frequency-response characteristics
are not obtained from such a circuit.
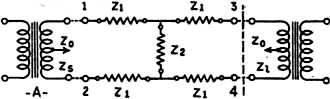
Fig. 7 - Diagram of an attenuator pad.
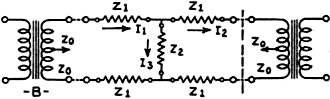
Fig. 8 - A resistive attenuator network.
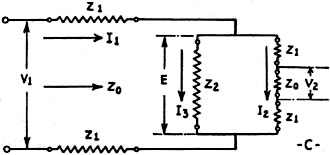
Fig. 9 - Equivalent circuit of Fig. 8.
If the load impedance Z1 (see Fig. 3) exactly equals the source impedance
Zs, then the source impedance Zs is said to be working into its "image impedance,"
for in such a case, there is no reflection of energy from the load impedance back
into the line.
If an attenuator is now inserted into the transmission line between the source
and the load, it must be so designed that the impedance of the attenuator must in
no way upset the impedance match between the source and the load. If then, when
the attenuator is working in the transmission line, the impedance "looking" into
the source (from the line) exactly equals the impedance "looking" into the load
(from the line), then the pad is said to be working between its "image impedances,"
and no energy will be reflected back at any point along the line, as the impedances
looking in either direction along the line are exactly equal. In such a case, no
reflection losses will occur at any junction points throughout the line, and practically
ideal transmission characteristics are obtained, except for such losses as arise
from the effects due to the length of line over which the energy is fed. (The losses
due to length of line will not be considered in these papers. It is assumed that
the voltage at the source is the voltage appearing across the 1-2 terminals, (See
Fig. 7) of the pad, and the voltage at the 3-4 terminals is the voltage across
the load).
Design Considerations
In order to maintain the same impedances in either direction, the pad must be
designed in such a manner, that when looking into the 1-2 terminals, the combined
(resultant) impedance of the attenuator and the load must exactly equal the source
impedance. Also, when looking into the 3-4 terminals, the combined (resultant) impedance
of the attenuator and the source must exactly equal the load impedance. These last
two statements described the "characteristic impedance" of the circuit when looking
into both the source and load ends of the line.
In order therefore, to fulfill the circuit requirements for image impedance,
and characteristic impedance, the two must be equal, and upon completion of the
design of the pads, this will readily be seen.
Having discussed the various problems that must be considered from an impedance
matching standpoint, our next problem is to analyze the manner in which pads function
in the transmission circuit.
It is the purpose of the writer to lead up to the actual design of the pads by
the method of "approach." For, having threshed out the various problems associated
with the circuit, the design of the pads is then reduced to the simple process of
substitution into the working formulae for the pad under consideration.
Continuing now with an analysis on pads, it was stated in the first part of this
paper, (May, 1932 issue) that pads are used to control the level of the energy entering
the load. We are principally interested then, in determining the relative amount
of current and voltage appearing at the load. In Fig. 8 is shown an "H"-type
network working between a source impedance Zo and a load impedance Zo. Now, referring
to Fig. 9, which is the equivalent circuit of Fig. 8, it can be seen that
if we wish to keep the current I2 and the voltage V2 at the load at certain fixed
values, with a constant voltage V1 impressed across the input terminals of the pad,
the values of the resistances used in the pad would have certain predetermined values
in order to give the correct loss between the input and output terminals. The values
of these resistances are determined by the impedances between which the pad is working
and the ratio of the current or voltage on the input side, to the current or voltage
on the output side of the pad.
Let us return now to our own problem under consideration, that of designing a
pad to give a 20·decibel loss. We have determined that if the voltage is reduced
to 1/10 of its original value, or in the order of 10 to 1, the voltage ratio is
10, and expressed logarithmically this loss is 20 decibels.
Suppose we wish to reduce the voltage only a small amount, or in the ratio of
1.12 to 1. We would then have only a 1-decibel loss in the circuit, which is comparatively
small. Now suppose we wish to set up a large loss, in the order of 100 to 1. We
then would have a 40-decibel loss. Taking these three cases of 1-, 20-, and 40·decibel
losses, and impressing various values of voltage V1 at the input terminals, let
us see how the pads that we would have to design would vary, in order to keep a
constant voltage V2 at the output terminals of the pad. In Table 3 are given the
values of resistances as used in the series and shunt arms of "H"-type pads, when
working between 200-, 500-, and 600 ohm impedances.
Now, using the 20-decibel loss as a reference level and referring to this table,
it is seen that to obtain a 20·decibel loss the series arm, Z1 is 82 ohms, and the
shunt arm Z2 is 40.4- ohms, when working between two 200-ohm impedances. With these
constants, the output voltage would be 1/10 the value of the input voltage. Or,
if the input voltage is 1.5 volts, the output voltage would be 0.15-volts, and the
voltage would have been dropped 1.35 volts.
Now assume that the input voltage is 0.168 volts and we still wish to maintain
the output voltage V2 at 0.15-volts. The voltage ratio, is 0.168/0.15 or 1.12; or,
a 1-decibel loss is obtained in the circuit. From Table 3, for a 1-decibel loss,
the series arm Z1 is only 5.65 ohms, whereas, the shunt arm Z2 goes up to 1760 ohms.
From the simple laws of current flow, this can be understood; for to obtain only
a 1-decibel loss, we do not wish to introduce a large amount of series resistance,
as this would impede the current flow, which is what we wish to avoid. The voltage
drop in this case is only 0.168 minus 0.15 or 0.018-volts. Therefore, the series
arm Z1 must be very small, and is but 5.65 ohms. Also, the shunt arm Z2 must be
very large, so that very little current will be bypassed or shunted from the load,
and as can be seen, its value is large, being 1760 ohms.
Now comparing the 20-decibel loss to the 1-decibel loss, in order to obtain the
same output voltage with different input voltages, the series arm Z1 for a 1-decibel
loss is only 5.65 ohms, and for a 20-decibel loss is 82 ohms. The shunt arm Z2 for
a 1-decibel loss is 1760 ohms, and for a 20-decibel loss is only 40.4 ohms. Therefore,
to obtain a fairly large loss, (such as 20 decibels), the series arm is quite large
and the shunt arm comparatively small (compared to the load impedance.) In this
case, the current will be impeded by the large series arm, thereby dropping the
voltage considerably, and at the same time shunting it from the load by the comparatively
small shunt arm, thus creating the fairly large loss desired.
For a small loss such as a 1 decibel, the series arm is very small and the shunt
arm very large as compared to the load impedance. In this case, very little voltage
drop is encountered in the series arm, and since the shunt arm is very large, very
little current will be shunted from the load. Therefore, practically all of the
original current will enter the load, thereby obtaining the small loss desired.
Now if the input voltage is 15 volts and we want to maintain the output voltage
V2 15 at 0.15-volts, the voltage ratio is 15/0.15 or 100, and the decibel loss is
40. This means we need to set up a very large loss, for the voltage is to be dropped
from 15 volts to .15-volts, a decrease of 14.85 volts. To do this, we should need
a very large series resistance and a very small shunt resistance, so that practically
all of the current will be prevented from entering the load by (1) the large series
arm, and (2) the very small shunt arm. Referring to Table 3, it can be seen that
to cause a 40-decibel loss, the series arm Z1 is 99 ohms and the shunt arm Z2 is
but 2 ohms, which exactly follows the reasoning as given above.
Comparing this 40 decibel loss to the 20 decibel loss, the series arms for the
20- and 40-decibel losses are 82 ohms and 99 ohms respectively, and the shunt arms
40.4 and 2 ohms respectively. The values for the series arms are such that a large
series voltage drop is encountered in them, being greater in the 40 decibel case,
as would be expected. The shunt arms are quite different.
In the 20-decibel loss, the shunt arm is practically 1/5 of the value of the
load impedance, so that only a comparatively large bypass effect of current from
the load is obtained; whereas, 1 in the 40-decibel loss, the shunt arm is only 1/50
of the value of the load impedance, thereby shunting practically all of the current
from the load. For a very large loss then, the series arms are very large and the
shunt arms very small in comparison to the load impedance. By inspecting Table 3,
it will be seen that the various values of the series and shunt arms necessary to
give certain losses follow the simple laws of current flow; in that large-decibel
losses require large series arms and small shunt arms in comparison to the value
of the load impedance, and that small decibel losses require small series arms and
large shunt arms in comparison to the load impedance.
Posted October 28, 2020
(updated from original post on 9/15/2015)
|













