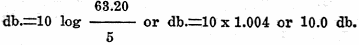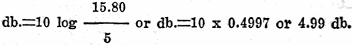|
May 1936 Radio-Craft
 [Table
of Contents] [Table
of Contents]
Wax nostalgic about and learn from the history of early electronics.
See articles from Radio-Craft,
published 1929 - 1953. All copyrights are hereby acknowledged.
|
Arithmophobia (a real word) is likely the root cause of of decibelphobia
(that one's made up), a condition that causes some otherwise rational people to
curl in the fetal position in an attempt to avoid the topic. As with most subjects,
the more often you engage in using a term, the more comfortable you become with
it. Technicians and engineers who deal in voltage and power levels in terms of dividing
quantities or transmitting them from one location to another would find conversation
and writing without the use of decibels quite inconvenient. It is tempting to point
out that using decibel units to express ratios or relative levels, thereby permitting
use of simple addition and subtraction rather than multiplication and division,
respectively, is no different than using logarithms to do the same with any number
in general. However, logarithms are lost on most people as well. Historically, logarithms
were so important in science and mathematics that large volumes were created to
facilitate rapid multiplication and division of numbers.
Just as it is unreasonable to go to a foreign country and expect the indigenous
people to adapt their common language to accommodate your lack of knowledge*, if
you expect to live in the realm of the RF and microwave world citizens, developing
fluency in decibels is essential to a successful, productive existence. This article
from a 1936 edition of Radio-Craft is as good a place to start as any.
* Except for the case of the hoards crossing the U.S. southern border illegally
with the expectation that we'll happily accommodate their native language and even
provide all governmental communication in that language while berating protesting,
legal citizens who are forced to pay for the policy. Oh, wait, that's what we do >:(
Decibel Level vs. Decibel Gain - Do not miss this lucid explanation!

Fig. 1 - The factors involved in db. gain and level.
S. L. Canterbury
Amplifiers are rated according to the number of watts output they can handle
without distortion. The output depends upon the size and design of the amplifier.
This output tells what volume of sound will come from a system and the area that
can be covered with the installation.
The amplifier performs but one important function: to receive the voice of the
speaker or music and raise the volume to a much higher level so that the sound energy
may be heard by many people over a fairly large area.
Basic Ratings
Before the gain (amplification) of an amplifier can be measured it is necessary
to select some unit of measurement. As the output of the amplifier is rated in terms
of watts it would be logical to measure the input in terms of watts also. Now the
effect of sound energy on the ear is not a direct (arithmetic) function but varies
in an exponential way. Therefore, the gain of an amplifier is expressed in the same
way, by means of logarithms. The expression is given by the formula:
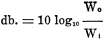
where db. represents the unit of transmission or amplification-the decibel; W0
is the power output; and Wi is the power input. The formula states that
the "decibel gain" is equal to ten (10) times the logarithm of the efficiency of
the amplifier. Efficiency is here used in connection with sound energy and does
not mean the electrical efficiency which is usually very low. The above formula
will hold at all times in rating amplifiers.
Amplifiers can also be rated in terms of currents and impedances. Referring to
Fig. 1, the formula is
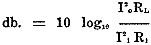
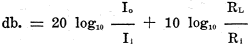
If the resistance of the input impedance equals the load resistance, the 'last
term becomes zero and the first term gives the decibel gain. In some designs, however,
the second term may be considerable and must not be neglected in such cases.
The gain may also be rated in terms of input and output voltages, provided the
input and output reactances are equal to zero; that is, when both impedances are
resistance only. The formula is:
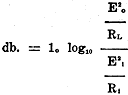
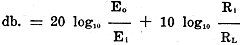
Again the last term equals zero, if the input and output resistances are equal.
The "Zero Level"
Sound and noise levels are usually expressed in decibels and not in watts, therefore,
a reference level of zero decibels must be set. For convenience, engineers have
arbitrarily taken the output of a common-battery telephone transmitter (when spoken
into with a loud voice) as zero level. This equals 0.01-watt or 10 milliwatts. The
output of a standard transmitter, used by telephone engineers is also 10 milliwatts.
Thus in telephone work zero level has been set at 10 milliwatts, but in radio work
it will be noticed that the articles in the past have always mentioned the reference
level and is not universally standard. The tendency among radio engineers is to
refer the system to a zero level of 0.006-watt or 6 milliwatts and throughout this
article all levels will be with respect to 6 milliwatts. It 's of very little importance
whether the level is 10 or 6 milliwatts as long as one or the other is taken. as
standard!
By using 6 milliwatts as zero level, amplifiers may be rated at an energy level
of a certain. number of decibels. This is desirable because the ear responds to
sound in a logarithmic manner. This can be illustrated by the following example.
If an amplifier delivers 6 watts output it has a level of:
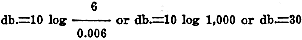 . .
Now, if the output is doubled, the ear will notice an increase in volume but
not twice as great as the 6 watts output because the ear will respond as the increase
in decibels and not as the increase in watts output. Thus,
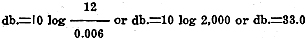
The ear did not detect the increased volume in a direct ratio, but as the logarithm
of the ratio. Therefore, if this zero reference level were not used, the amplifier
control set at 30 db. gain would not give any indication of the volume of the output
unless the input were known. With the control marked in decibels above zero level,
the 30 db. setting would indicate an output of 12 watts.
A commercial amplifier rated at 26 watts out-put has an energy level, at full
output, expressed in decibels equal to:
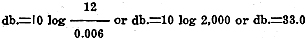
Now 'it is stated in the catalog that this amplifier has a gain of 96.4 db. Where
do the extra 60 decibels come from? The answer to this question will become evident
after the microphone output has been considered.
Allowance for Mike "Level"
Different types ·of microphones have different energy output levels, but most
commercial-type carbon-button microphones give an energy level of -50 to -80 db.
When the speaker (source of sound) is near the mike, a good average is the -60 db.
level. The mike, therefore, lowers the energy level that it receives and it is the
function of the amplifier to raise the voice level from -60 db. back to zero level
and still higher in order to have appreciable output at the loudspeaker. After the
sound has passed through the mike, it is at a very low level and has very little
energy. The actual power impressed on the amplifier input, after passing through
the mike, can be found as follows: -60 = 10 log R; where R is the ratio of mike
output to mike input, and here it is assumed that zero level is impressed upon the
mike. 40.0000 - 100 = 10 log R or 4.0000 - 10 = log R or
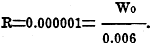 . Therefore W0
= 0.006-microwatt. . Therefore W0
= 0.006-microwatt.
Thus the input of zero level to the mike is lowered to -60 db. in passing through
the mike and the power that the amplifier begins with is very small. The entire
gain is therefore 96.4 db. as the amplifier ends up with a 36.4 db. level. In amplification
work it is desirable to know what level above zero the amplifier will raise the
sound of the speaker's voice, and, therefore, the maximum reading on the control
should be 36.4 db. and not 96.4 db. A high-gain amplifier when used with a very
poor mike may give but little amplification. For example, suppose the mike had a
loss of 76.4 db. This would leave a gain of 20 db. above zero. The output would
be far below the rated 26 watts and would be equal to:
20 = 10 log R or 2.0000 = log R or
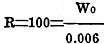 or the output W0
equals 0.6·watt. After all, the decibel gain is not so important. It is the decibel
level above zero that counts. It is well to point out here that there is a limit
to the over-all gain that an amplifier may have, as explained in Radio-Craft July
1935, page 10. or the output W0
equals 0.6·watt. After all, the decibel gain is not so important. It is the decibel
level above zero that counts. It is well to point out here that there is a limit
to the over-all gain that an amplifier may have, as explained in Radio-Craft July
1935, page 10.
The energy required to operate the amplifier is 90 watts, while the output is
but 26 watts. The efficiency is therefore

This may be expressed in decibels as would be done if used in connection with
telephone work.
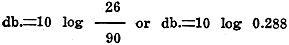 or or
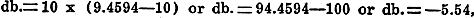 which represents a loss. which represents a loss.

Table 1 - Decibel vs. percentage loss.
The accompanying, Table I lists the efficiency for certain decibel gains or losses.
The table's use can be demonstrated by means of the following examples. It is well
to point out that the table may be used for any value of decibel gain. Suppose the
efficiency at 15 db. gain is to be found. Fifteen decibels equal 10 db. plus 5 db.
but the resulting efficiency is the product of the efficiencies at 10 db. and 5
db. A 15 db. gain gives an efficiency of 10 x 3.16 = 31.6 or 3,160 per cent.
A Db. Gain in - Dollars!
Let us now use this 15 db. gain in a problem. A man starts out with $2 and at
the end of two weeks he has a 15 db. gain which is an efficiency of 3,160 per cent.
Therefore, at the end of two weeks the man has $63.20. The man's son also has a
decibel gain of 15 at the end of two weeks but he started with 50 cents. His efficiency
is also 3,160 per cent but instead of having $63.20, like his father, the boy has
only $15.80. Again it is seen that the db. gain is not as important as the db. level
above a certain reference point. Suppose the reference point chosen by the two is
$5.00, and this is zero db. level. The man at the end of 2 weeks, has a level of:
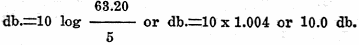
The boy has a db. level of:
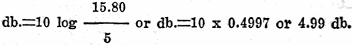
level which shall be called a 5 db. level.
With the level above, as the reference point, it is at once evident that the
father has more money than his son. Both still have the same gain, however. In this
case the man began with a -5 db. level and finished with 10 db., a gain of 15. The
boy began with a -10 db. level and ended with a 5 db. level which is also a 15 db.
gain.
Posted January 3, 2022
(updated from original post on 4/24/2015)
|









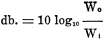
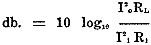
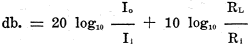
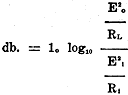
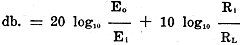
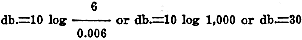 .
.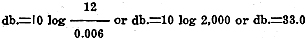
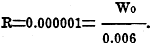 . Therefore W0
= 0.006-microwatt.
. Therefore W0
= 0.006-microwatt. 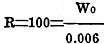 or the output W0
equals 0.6·watt. After all, the decibel gain is not so important. It is the decibel
level above zero that counts. It is well to point out here that there is a limit
to the over-all gain that an amplifier may have, as explained in Radio-Craft July
1935, page 10.
or the output W0
equals 0.6·watt. After all, the decibel gain is not so important. It is the decibel
level above zero that counts. It is well to point out here that there is a limit
to the over-all gain that an amplifier may have, as explained in Radio-Craft July
1935, page 10. 
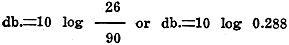 or
or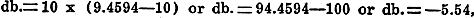 which represents a loss.
which represents a loss.