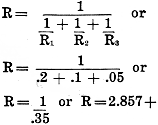|
November 1935 Short Wave Craft
 [Table
of Contents] [Table
of Contents]
Wax nostalgic about and learn from the history of early electronics. See articles
from Short Wave Craft,
published 1930 - 1936. All copyrights hereby acknowledged.
|
As mentioned many times
in the past, some things never change regarding the basics of electricity and electronics.
Resistance, inductance, and capacitance (termed "capacity" here) are examples and
are addressed in this last of a three-part series which appeared in 1935 issues
of Short Wave Craft magazine. When first starting out in this science,
an effective introduction to the fundamentals can often determine whether a person
sticks with it or finds another area of interest to pursue as a hobby and/or vocation.
Analogous examples of voltage and water pressure, resistance and the diameter of
a water hose, inertia in a spinning mass opposing a change in rate and an inductor
opposing a change in current, etc., are presented along with some good sketches
of the principles.
See Part 1,
Part
2, and Part 3
Radio Amateur Course
No. 3 - Resistance, Inductance, and Capacity
This is the third lesson in our Amateur Radio Course and it will deal with resistance,
capacity, and inductance, as concerned with radio circuits. In order to understand
how a vacuum tube oscillates, how tuned circuits work, and the function of a tuning
condenser, it is necessary to become familiar with these three very important subjects.
Resistance
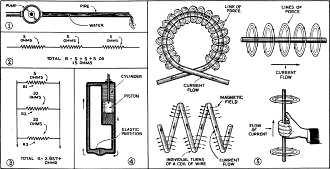
In Fig. 1 we have a diagram showing how the size of a pipe
governs the amount of water that can be forced through it. In Fig. 2 we have
resistors connected in series. In Fig. 3 they are connected in parallel; the
formulae are given in the text. Fig. 4 is the hydraulic analogy for the action
of a condenser when alternating current is applied to it. Fig. 5 shows the
magnetic fields and direction of current flow in straight wires and coils; also
the right-hand rule is given, where, if the thumb points in the direction of the
current flow, the four fingers will curve around the conductor in the direction
of the magnetic field.
When electrical current flows through a wire or some other conducting medium
it encounters resistance or opposition, the same as the flow of material substances.
For instance, a certain amount of water can be forced through a length of one-inch
pipe with a definite pressure. In other words, the size of the pipe offers resistance
to the flow. The larger the pipe becomes, the greater the amount of water can be
forced through it at a definite pressure, or the larger the pipe becomes, the less
its resistance would be.
This holds true in conductance of electricity inasmuch as a fine wire or conductor
offers a greater amount of resistance than a heavy conductor. The resistance of
a conductor is inversely proportional to its cross sectional area and with some
materials, in fact most of them, the resistance also increases as the temperature
rises.
In dealing with resistance in electrical circuits, we have what is known as Ohm's
Law. In Ohm's Law, we have to consider three things: First, the flow of electricity,
which is current; second, the force or pressure, which is voltage; and third, the
resistance which the flow of electricity encounters. Three letters are assigned
to the above, and they are:
I = Current
E = Voltage (EMF)
R = Resistance
The formulas for finding the resistance, voltage, or current, where either two
of the three are known are as follows:
I = E/R
R = E/I
E = R x I
When two or more resistors are connected in series the total value of the resistance
is the sum of all the resistors. In other words, three 5-ohm re-sistors in series
would have a total resistance of 15 ohms.
However, when resistors are connected in parallel the method of calculation is
a bit more complicated. For instance, if we have three resistors connected in parallel,
one has the resistance of 5 ohms, another of 10, and another of 20. The formula
for expressing this is:
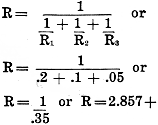
Capacity
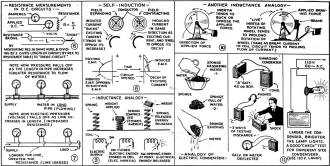
Fig. 6 above shows measurement of resistance. Fig. 7
shows how pressure or voltage decreases with increase in resistance to flow of water
or electric current. Fig. 8 shows action of expanding and contracting magnetic
fields. Fig. 9 shows mechanical "spring" analogy for inductance; Fig. 10
- Fly-wheel analogy of inductance. Fig. 11 - Analogies for condenser.
Most of us are familiar with the now well-known condenser which is an instrument
capable of storing up a certain amount of electricity and consists of two or more
plates placed adjacent to each other, with insulation of either air or some other
insulating medium. When a constant direct voltage is applied between the plates
of a condenser, current will flow into the condenser, until the condenser becomes
charged to its maximum capacity. The current then ceases to flow and the condenser
is charged. Then, after the source of electricity (battery for example) is removed
from the circuit, the condenser will hold its charge until, due to its inherent
(conductivity of dielectric) resistance, the power is dissipated.
If the insulation is mica or parafined (waxed) paper, the condenser will hold
its charge for a considerable length of time. In large condensers of one or two
microfarads the charge may remain in the condenser for several hours. This can be
proved by short-circuiting the two terminals of the condenser and noting the spark,
or an ammeter could be connected across the condenser and it would indicate the
current flowing until the condenser was completely discharged and the power dissipated.
The unit of capacity is a farad; however, in radio work, we use considerably smaller
units in our condensers.
A microfarad is one millionth of a farad, and one micro-micro-farad is one millionth
of a microfarad. The most important part of a condenser is the dielectric or insulating
material because, contrary to popular belief, it is in the dielectric that the charge
resides. When a condenser is charged, the dielectric opposes the setting up of an
electric displacement of an electric field in the dielectric and the charge is said
to be the energy of the charging source stored up as electro-static energy in the
dielectric.
A simple analogy for the action of an electrical condenser is a sponge, which
absorbs water when placed in a cupful of it, for example, and afterwards if pressure
is exerted on the sponge, then it gives up the water stored in it. It requires 1
coulomb (ampere-second) to charge a condenser of 1 farad to a potential of 1 volt.
A condenser having a capacity of 1 mf. (1 mf. = 1 millionth of 1 farad) requires
a charge of 1 millionth of 1 coulomb to charge it to a potential of 1 volt.
Inductance
The coils used in radio circuits are called inductances or inductors. In the
drawings we see how an electro-magnetic field may be produced around the wire when
a current is passed through it. If the flow of current through a conductor is constant
(D.C.) a steady electro-magnetic field is produced around the conductor. However,
when alternating current (abbreviated A.C.) flows through a conductor, the current
flow is constantly changing and likewise the field is changing.
When current begins to flow through a wire the circular electro-magnetic field
originates at the center of the conductor and travels outwardly away from this center
in constantly increas-ing diameters and of course, extends into the space surrounding
the wire. Until this field becomes of larger diameter than the wire, it causes a
second current to flow in opposition to the main current.
When the current flow through the wire decreases or stops, the circular fields
collapse and are then said to cut the wire in ever-diminishing diameters. This induces
a current in the opposite direction to the field but in the same direction as the
original (exciting) applied current, tending to prolong the flow of the exciting
current.
This property of a coil or conductor to act upon itself or another inductor in
close proximity to it, is called inductance. The unit of inductance is the henry
and in most formulas it is usually designated by the symbol "L." A henry is the
inductance of a circuit in which the induced E.M.F. is one volt; when the (varying)
current travels at the rate of one ampere in one second. Usually in radio circuits,
inductance values are indicated as one thousandth of a henry or - one milli-henry;
a millionth of a henry is known as a micro-henry. The physical dimensions and form
of a circuit, determine the amount of inductance and it is for this reason that
our radio circuits consist of coils rather than straight wire, because a greater
amount of inductance can be obtained by coiling the wire, also allowing considerably
less D.C. resistance because less wire is used. A straight wire, of course, would
have less inductance than one of the same length which was coiled.
Induction subdivides into two branches - self and mutual induction. If the current
passing through a coil, for example, is rising from zero to maximum value, such
as when the circuit is closed from a battery, (or the first half of an alternation
of an alternating current) the magnetic field around the wire is expanding and while
this is taking place there is induced in the conductor a counter-current (and counter
e.m.f. or voltage) which tends to buck or oppose the current (and voltage) which
is producing the field.
As one of the diagrams shows there is electrical energy stored up in an inductive
circuit, just as if you had compressed a spring. The opening of the circuit, and
spark at the switch, corresponds to releasing the compressed spring and heaving
off the weight.
Another analogy is the flywheel. The inertia of the wheel opposes any force to
set it in motion; once in motion, the energy tied up in the wheel tends to keep
it going, if any effort is made to stop it.
Let us consider for a moment now the next phase of the action taking place when
the circuit is opened or when the second half of the alternation of an applied A.C.
is taking place. Now the magnetic field around the wire or turns of wire comprising
the coil is contracting and while this occurs, the lines of magnetic force are cutting
the wire in the opposite direction and a current of opposite sign is induced in
the wire, this current being in the same direction as the applied (exciting) current
which is flowing around the wire and creating the magnetic field.
In other words, the self-induced e.m.f. is in the opposite direction, while the
field is expanding about the wire, and tends to oppose it while the opposite is
the case when the field is contracting and the current is then in the same direction
or aids the inducing current and acts to prevent its decay.
It will be apparent, of course, that while the current is varying in strength
or let us say increasing, the field about the coil is expanding, and the lines of
magnetic force expanding out from the coil composed of a number of turns, will induce
a current by induction in a second coil, placed near or adjacent to the first or
exciting coil.
If we term the exciting coil No. 1, and the adjacent unconnected coil as No.
2, coil 2 is said to have a current induced in it by electro-magnetic induction.
As the magnetic field in coil No. 1 subsides, the magnetic lines of force surrounding
coil No.2 also subsides. At the same time these lines of force cut across the turns
in coil No. 1 and induce therein an e.m.f. or voltage (also a current) and thus
we have a third e.m.f. set up by induction.
To begin with, we have the original exciting e.m.f. in coil 1; secondly we find
an induced e.m.f. in coil 2; and thirdly, there is a reeinducedde.m.fe.m.fe.m.f.
in coil 1, due to the reaction of the magnetic field surrounding coil 2, and this
effect is what is known as mutual induction.
The usual radio tuned circuit consists of a coil and a condenser, namely: inductance
and capacity. Coils or inductances have what is known as inductive reactance, while
condensers have capacity reactance. When the capacity reactance minus the inductive
reactance equals zero, at some certain frequency, the circuit is said to be in resonance.
When the condition known as Resonance has been established in any given circuit
whether a series or parallel type circuit: then we know that the inductive and capacitive
reactance are equal, and that they balance each other. When this condition has been
achieved their reactive effect upon the circuit is zero. Under these conditions,
or when the circuit has been made resonant, (by the proper adjustment of the capacity
and the inductance of the circuit) any current flowing in the circuit due to an
applied e.m.f. will be that due simply to the ohmic or direct current resistance
in the circuit. Expressed another way, the current passing through such a resonant
circuit will be given by the expression: I = E/R.
The difference between the capacitive and inductive reactance of a circuit at
some frequency is called the impedance. However, at resonance, this is always zero,
and the losses in the circuit are due only to the usual D.C. resistance of the circuit,
through which the currents are flowing.
In Fig. 4 we see a hydraulic analogy of current flowing into a condenser.
When the piston is moved forward, the elastic partition will bend or become curved
but will not allow the liquid to be transferred from one side to the other.
In the fourth lesson of our Amateur Radio Course, which will appear in the following
issue of Short Wave Craft, the action and principles involved in Regeneration and
Oscillating Vacuum Tube circuits will be discussed. Don't miss the next installment.
Posted December 10, 2020
(updated from original post on 6/21/2015)
|