|
 Capacitors are passive devices used
in electronic circuits to store energy in the form of an electric field. They are the compliment of
inductors, which store energy in the form of a magnetic field. An ideal capacitor
is the equivalent of an open circuit (infinite ohms) for direct currents (DC), and presents an impedance (reactance) to
alternating currents (AC) that depends on the frequency of the current (or voltage). The reactance (opposition to current
flow) of a capacitor is inversely proportional to the frequency of the of the signal acting on it. Capacitors were originally
referred to as "condensers" for a reason that goes back to the days of the Leyden Jar where electric charges were thought
to accumulate on plates through a condensation process. Capacitors are passive devices used
in electronic circuits to store energy in the form of an electric field. They are the compliment of
inductors, which store energy in the form of a magnetic field. An ideal capacitor
is the equivalent of an open circuit (infinite ohms) for direct currents (DC), and presents an impedance (reactance) to
alternating currents (AC) that depends on the frequency of the current (or voltage). The reactance (opposition to current
flow) of a capacitor is inversely proportional to the frequency of the of the signal acting on it. Capacitors were originally
referred to as "condensers" for a reason that goes back to the days of the Leyden Jar where electric charges were thought
to accumulate on plates through a condensation process.
The property of capacitance that opposes a change in voltage is exploited for the purpose of conducting signals with
a higher frequency component while preventing signals of lower frequency components from passing. A common application of
a capacitor in an RF (radio frequency) circuit is where there is a DC bias voltage that needs to be blocked from being present
in a circuit while allowing the RF signal to pass. DC power supplies use large capacitance values in parallel with the output
terminals to smooth out low frequency ripples due to rectification and/or switching waveforms.
  When used in series (left drawing) or parallel (right drawing) with its
circuit compliment, an inductor, the inductor-capacitor combination forms a circuit that resonates at a particular frequency
that depends on the values of each component. In the series circuit, the impedance to current flow at the resonant frequency
is zero with ideal components. In the parallel circuit (right), impedance to current flow is infinite with ideal components.
Real-world capacitors made of physical components exhibit more than just a pure capacitance when
 present in an AC circuit.
A common circuit simulator model is shown to the left. It includes the actual ideal capacitor with a parallel resistive
component ('Leakage') that responds to alternating current. The equivalent DC resistive component
('ESR') is in series with the ideal capacitor and an equivalent series inductive component
('ESL') is present due to metal leads (if present) and characteristics of the plate surfaces.
This inductance, in combination with the capacitance, creates a resonant frequency at which point the capacitor looks like
a pure resistance. present in an AC circuit.
A common circuit simulator model is shown to the left. It includes the actual ideal capacitor with a parallel resistive
component ('Leakage') that responds to alternating current. The equivalent DC resistive component
('ESR') is in series with the ideal capacitor and an equivalent series inductive component
('ESL') is present due to metal leads (if present) and characteristics of the plate surfaces.
This inductance, in combination with the capacitance, creates a resonant frequency at which point the capacitor looks like
a pure resistance.
As the operational frequency is increased past resonance (aka self-resonant frequency, or SRF),
the circuit behaves as an inductance rather than a capacitance. Hence, careful consideration of the SRF is required when
selecting capacitors. SPICE-type simulators use this or an even more sophisticated model to facilitate more accurate calculations
over a wide range of frequencies.
Equations for combining capacitors in series and parallel are given below. Additional equations are given for capacitors
of various configurations. As these figures and formulas indicate, capacitance is a measure of the ability of two surfaces
to store an electric charge. Separated and isolated by a dielectric (insulator), a net positive charge is accumulated on
one surface and a net negative charge is stored on the other surface. In an ideal capacitor, charge would be stored indefinitely;
however, real world capacitors gradually lose their charge due to leakage currents through the non-ideal dielectric.
These calculations are included in the free
Espresso Engineering Workbook.

 Total capacitance of series-connected capacitors is equal to the reciprocal of the
sum of the reciprocals of the individual capacitances. Keep units constant.
|
|


Capacitance (C, in Farads) of two equal-area parallel plates is the product of the area (A, in meters) of one plate,
the distance (d, in meters) separating the plates, and the dielectric constant (ε, in Farads per meter) of the space
separating the plates. ε, the total dielectric constant, is the product of the dielectric constant of free space, ε0,
and the relative dielectric constant of the material, εr. Note that units of length and area can be metric
or English so long as they are consistent.
|


Length (l) in meters
|
 
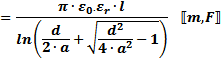
Length (l) in meters
|


|

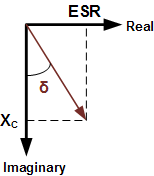 Dissipation Factor (DF), aka Loss Tangent (tan δ) is interchangeably defined as
the reciprocal of the Quality Factor (QF) or the ratio of the equivalent series resistance (ESR) and the capacitive reactance
(XC). It is a measure of the loss rate of stored charge. DF is typically used in low frequency applications while
tan δ is more often used in high frequency applications. Dissipation Factor (DF), aka Loss Tangent (tan δ) is interchangeably defined as
the reciprocal of the Quality Factor (QF) or the ratio of the equivalent series resistance (ESR) and the capacitive reactance
(XC). It is a measure of the loss rate of stored charge. DF is typically used in low frequency applications while
tan δ is more often used in high frequency applications.
|
|

 Total capacitance of parallel-connected capacitors is equal to the sum of the individual
capacitances. Keep units constant.
|
|
The following physical constants and mechanical dimensional variables apply to equations on this page. Units for equations
are shown inside brackets at the end of equations; e.g.,  means lengths are in inches and inductance is in Henries.
If no units are indicated, then any may be used so long as they are consistent across all entities; i.e., all meters, all µF,
etc. means lengths are in inches and inductance is in Henries.
If no units are indicated, then any may be used so long as they are consistent across all entities; i.e., all meters, all µF,
etc.
C = Capacitance L = Inductance W = Energy εr = Relative permittivity (dimensionless)
ε0 = 8.85 x 10-12 F/m (permittivity of free space) µr
= Relative permeability (dimensionless) µ0 = 4π x 10-7 H/m (permeability of free space)
1 meter = 3.2808 feet <—> 1 foot
= 0.3048 meters 1 mm = 0.03937 inches <—> 1 inch
= 25.4 mm
Also, dots (not to be confused with decimal points) are used to indicate multiplication
in order to avoid ambiguity.
|
 Capacitive reactance (XC,
in Ω) is inversely proportional to the frequency (ω, in radians/sec, or f, in Hz) and capacitance (C, in Farads).
Pure capacitance has a phase angle of -90° (voltage lags current with a phase angle of 90°).
|
 Charge (Q, in coulombs) on a capacitor's
plates is the product of the capacitance (C, in Farads) and the voltage (V, in volts) across the device.
|
 Energy (W, in Joules) stored in a capacitor
is half the product of the capacitance (C, in Farads) and the voltage (V, in volts) across the device.
|
 Current does actually flow 'through' an
ideal capacitor. Rather, charge stored on its plates is given up to the connected circuit, thereby facilitating current
flow. Conversely, a net voltage applied to its plates causes a current to flow in the connected circuit as charge accumulates
on the plates.
|
 Quality factor is the dimensionless
ratio of reactance to resistance in a capacitor.
|
|
Related Pages on RF Cafe - Capacitors &
Capacitance Calculations -
Capacitor
Color Codes - Capacitance Conversions -
Capacitor Dielectrics -
Standard Capacitor Values -
Capacitor Vendors -
The Noble Art of De-Coupling
|
















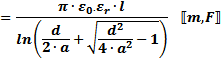



 Dissipation Factor (DF), aka Loss Tangent (tan δ) is interchangeably defined as
the reciprocal of the Quality Factor (QF) or the ratio of the equivalent series resistance (ESR) and the capacitive reactance
(XC). It is a measure of the loss rate of stored charge. DF is typically used in low frequency applications while
tan δ is more often used in high frequency applications.
Dissipation Factor (DF), aka Loss Tangent (tan δ) is interchangeably defined as
the reciprocal of the Quality Factor (QF) or the ratio of the equivalent series resistance (ESR) and the capacitive reactance
(XC). It is a measure of the loss rate of stored charge. DF is typically used in low frequency applications while
tan δ is more often used in high frequency applications.

 means lengths are in inches and inductance is in Henries.
If no units are indicated, then any may be used so long as they are consistent across all entities; i.e., all meters, all µF,
etc.
means lengths are in inches and inductance is in Henries.
If no units are indicated, then any may be used so long as they are consistent across all entities; i.e., all meters, all µF,
etc.






