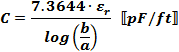Coaxial Cable Equations

Most professional engineers and technicians will never have the need to calculate the capacitance, inductance, or impedance of a coaxial cable since they are usually designing systems using well-defined components that are manufactured to exacting specifications. Students, hobbyists (Ham radio operators), and research types are probably the ones most likely to actually plug numbers into a calculator. For those people, I present these equations. Be very careful to realize that at frequencies far from DC, factors like skin depth and effective inner and outer conductor diameters may be significantly different than the physical measured values, and that can significantly affect real world results. Therefore, be sure to consult manufacturers' published data before making a final decision. I leave it to other sources to provide the complex equations needed to precisely model coaxial cables.

a = outside radius of inner conductor (inches)

b = inside radius of outer conductor (inches)

c = speed of light in a vacuum = 299,792 km/s = 186,282 mi/s

ε = dielectric constant = ε₀ * ε_r

ε₀ = permittivity of free space = 8.85419x10^-12 F/m

ε_r = relative dielectric constant

μ_r = relative permeability 

Capacitance (C)

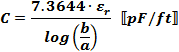
Note: a and b can be in any units of length as long as they are both the same.

Inductance (L)

Note: a and b can be in any units of length as long as they are both the same. However, l must be in the units shown.

Impedance (Z₀)

Note: a and b can be in any units of length as long as they are both the same. C has units of Farads and L has units of Henries.

Speed of Light (%c)

Note: V has the same length units as c.

Cutoff Frequency

Note: a and b must be in units of length shown.

Reflection Coefficient & VSWR

Note: Γ is unitless. VSWR is written as a VSWR:1 ratio.

Attenuation

Equations for coaxial cable attenuation used to be offered here, but while re-designing this page and attempting to verify the equations, I discovered (or probably re-discovered) that theoretical values versus published measured values for real-world cable varied a lot at every frequency. RG6 coax, for example, can have a loss at 1 GHz ranging from a little over 5 dB/100 feet to nearly 10 dB/100 feet, depending on the dielectric type, actual conductor and dielectric diameters, and it seems very importantly, the construction of the outer shield conductor. A single layer of loosely woven braid versus a one or more dense layer(s) of braid and one or more layer(s) of metal foil versus semi-rigid versus hardline coaxial cable makes calculation using a simple, one-size-fits-all equation impossible.

Therefore, I have removed the equations I used to have and instead recommend that you visit coaxial cable manufacturers' websites and consult their published data and decide what value of attenuation per foot, meter, etc., is most appropriate for your real-world applications.

Posted August 25, 2021
(updated from original post on 6/2/2005)

Related Pages on RF Cafe

- Coaxial Cable Specifications

- Capacitor Dielectrics & Descriptions

- Dielectric Constant, Strength, & Loss Tangent

- Conductor Bulk Resistivity & Skin Depths

- Coaxial Cable Equations

- Coaxial Cable Specifications

- Coaxial Cable Vendors

- Coaxial Resonator

- Skin Depth Calculator

- Coaxial Connector Usage Chart