Wireless communications make use of electromagnetic waves to send signals across
long distances. From a user's perspective, wireless connections are not particularly
different from any other network connection: your web browser, email, and other
applications all work as you would expect. But radio waves have some unexpected
properties compared to Ethernet cable. For example, it's very easy to see the path
that an Ethernet cable takes: locate the plug sticking out of your computer, follow
the cable to the other end, and you've found it! You can also be confident that
running many Ethernet cables alongside each other won't cause problems, since the
cables effectively keep their signals contained within the wire itself. But how
do you know where the waves emanating from your wireless device are going? What
happens when these waves bounce off objects in the room or other buildings in an
outdoor link? How can several wireless cards be used in the same area without interfering
with each other? In order to build stable high-speed wireless links, it is important
to understand how radio waves behave in the real world.
What Is a Wave?
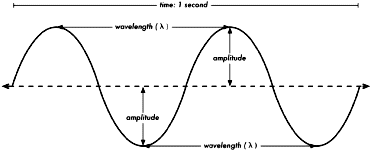
Figure RP 1: Wavelength, amplitude, and frequency. For this wave,
the frequency is 2 cycles per second, or 2 Hz, while the speed is 1 m/s.
We are all familiar with vibrations or oscillations in various forms: a pendulum,
a tree swaying in the wind, the string of a guitar - these are all examples of oscillations.
What they have in common is that something, some medium or object, is swinging
in a periodic manner, with a certain number of cycles per unit of time. This kind
of wave is sometimes called a mechanical wave, since it is defined by the motion
of an object or its propagating medium.
When such oscillations travel (that is, when the swinging does not stay bound
to one place) then we speak of waves propagating in space. For example, a singer
singing creates periodic oscillations in his or her vocal cords. These oscillations
periodically compress and decompress the air, and this periodic change of air pressure
then leaves the singers mouth and travels, at the speed of sound.
A stone plunging into a lake causes a disturbance, which then travels across
the lake as a wave.
A wave has a certain speed, frequency, and wavelength.
These are connected by a simple relation:
Speed = Frequency * Wavelength
The wavelength (sometimes referred to as lambda, λ) is the distance measured
from a point on one wave to the equivalent part of the next (or, in a more technical
way, to the next point that is in the same phase), for example from the top of one
peak to the next.
The frequency is the number of whole waves that pass a fixed point in a period
of time. Speed is measured in meters/second, frequency is measured in cycles per
second (or Hertz, represented by the symbol Hz), and wavelength is measured in meters.
For example, if a wave on water travels at one meter per second, and it oscillates
five times per second, then each wave will be twenty centimeters long:
1 meter/second = 5 cycles/second *W
W = 1 / 5 meters
W = 0.2 meters = 20 cm
Waves also have a property called amplitude. This is the distance from the center
of the wave to the extreme of one of its peaks, and can be thought of as the "height"
of a water wave. Frequency, wavelength, and amplitude are shown in Figure RP 1.
Waves in water are easy to visualize.
Simply drop a stone into the lake and you can see the waves as they move across
the water over time. In the case of electromagnetic waves, the part that might be
hardest to understand is: "What is it that is oscillating?" In order to understand
that, you need to understand electromagnetic forces.
Electromagnetic Forces
Electromagnetic forces are the forces between electrical charges and currents.
Our most direct access to those is when our hand touches a door handle after walking
on synthetic carpet, or brushing up against an electrical fence.
A more powerful example of electromagnetic forces is the lightning we see during
thunderstorms.
The electrical force is the force between electrical charges.
The magnetic force is the force between electrical currents.
Electrons are particles that carry a negative electrical charge. There are other
charged particles too, but it is the electrons that are responsible for most of
what we need to know about how radio behaves.
Let us look at what is happening in a piece of straight vertical wire, in which
we push the electrons from one end to the other and back, periodically. At one moment,
the top of the wire is negatively charged - all the negative electrons are gathered
there. This creates an electric field from the positively charged end to the negatively
charged one along the wire. The next moment, the electrons have all been driven
to the other side, and the electric field points the other way. As this happens
again and again, the electric field vectors (represented by arrows from plus to
minus) are leaving the wire, so to speak, and are radiated out into the space around
the wire.
What we have just described is known as a dipole (because of the two differently
charged poles, plus and minus, that are created in the straight vertical wire),
or more commonly a dipole antenna.
This is the simplest form of an omnidirectional antenna. The moving electric
field is commonly referred to as an electromagnetic wave because there is also an
associated magnetic field. A moving electric field, such as a wave, always comes
together with a magnetic field - you will not find one with out the other. Why is
this the case?
An electric field is caused by electrically charged objects.
A moving electric field is produced by moving electrically charged objects, such
as we have just described above in a dipole antenna.
Wherever electrical charges are moving, they induce a magnetic field. Mathematically,
this is formulated in Maxwell's equations:
https://en.wikipedia.org/wiki/Electromagnetic_field#Mathematical_description
Since the electrical and magnetic components are tied together in this way, we
speak of an electromagnetic field.
In practical wireless networking, we focus in the electrical component but there
be always a magnetic component as well.
Let us come back to the relation:
Speed = Frequency * Wavelength
In the case of electromagnetic waves, the speed is c, the speed of light.
c = 300,000 km/s = 300,000,000 m/s = 3*108
m/s
c = f * λ
Electromagnetic waves differ from mechanical waves in that they require no medium
in which to propagate. Electromagnetic waves will even propagate through perfect
vacuum.
The light from the stars is a good example: it reaches us through the vacuum
of space.
Phase
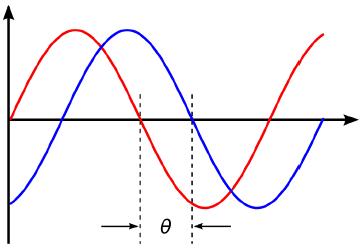
Figure RP 2: Phase difference between two waves
Later in this chapter, we will talk about concepts like interference, multipath
and Fresnel zones. In order to understand these, we will need to know about the
phase of a wave, or rather, phase differences between waves. Look at the sine wave
shown in Fig RP 1 - now imagine we have two such waves moving. These can be in exactly
the same position: Where the one has its peak, the other one also has a peak. Then,
we would say, they are in phase, or, their phase difference is zero. But one wave
could also be displaced from the other, for example it could have its peak where
the other wave is at zero. In this case, we have a phase difference. This phase
difference can be expressed in fractions of the wavelength, e.g. λ/4, or in degrees,
e.g. 90 degrees - with one full cycle of the wave being 360 degrees. A phase difference
of 360 degrees is the same as that of 0 degrees: no phase difference.
Polarization
Another important quality of electromagnetic waves is polarization. Polarization
describes the direction of the electrical field vector.

Figure RP 3: Vertically polarized electromagnetic wave.
If you imagine a vertically aligned dipole antenna (the straight piece of wire),
electrons can only move up and down, not sideways (because there is no room to move)
and thus electrical fields only ever point up or down, vertically. The field leaving
the wire and travelling as a wave has a strict linear (and in this case, vertical)
polarization. If we put the antenna flat on the ground, we would find horizontal
linear polarization.
Linear polarization is just one special case, and is never quite so perfect:
in general, we will always have some component of the field pointing in other directions
too. If we combine two equal dipoles fed with the same signal, we can generate a
circularly polarized wave, in which the electric field vector keeps rotating perpendicularly
to the wave's trajectory.
The most general case is elliptical polarization, in which the electric field
vector maximum value is not the same in the vertical and horizontal direction. As
one can imagine, polarization becomes important when aligning antennas. If you ignore
polarization, you might have very little signal even though you have the best antennas.
We call this polarization mismatch.
Much in the same way, polarization may also be used in a smart way, to keep two
wireless links independent and without interference, even though they might use
the same end points (or even share a common reflector) and therefore the same trajectory:
if one link is polarized vertically and the other horizontally, they will not "see"
each other. This is a convenient way to double data rates over one link using a
single frequency.
The antennas used in this kind of application must be carefully built in order
to reject the "unwanted" polarization, i.e. an antenna meant for vertical polarization
must not receive or transmit any horizontally polarized signal, and vice versa.
We say they must have a high "cross polarization" rejection.
The Electromagnetic Spectrum

Figure RP 4: The electromagnetic spectrum.
Electromagnetic waves span a wide range of frequencies (and, accordingly, wavelengths).
This range of frequencies or wavelengths is called the electromagnetic spectrum.
The part of the spectrum most familiar to humans is probably light, the visible
portion of the electromagnetic spectrum. Light lies roughly between the frequencies
of 7.5*1014 Hz and 3.8*1014 Hz, corresponding to wavelengths
from circa 400 nm (violet/blue) to 800 nm (red).
We are also regularly exposed to other regions of the electromagnetic spectrum,
including Alternating Current (AC) or grid electricity at 50/60 Hz, AM and FM radio,
Ultraviolet (at frequencies higher than those of visible light), Infrared (at frequencies
lower than those of visible light), X-Ray radiation, and many others.
Radio is the term used for the portion of the electromagnetic spectrum in which
waves can be transmitted by applying alternating current to an antenna. This is
true for the range from 30 kHz to 300 GHz, but in the more narrow sense of the term,
the upper frequency limit would be about 1 GHz, above which we talk of microwaves
and millimetric waves.
When talking about radio, many people think of FM radio, which uses a frequency
around 100 MHz. In between radio and infrared we find the region of microwaves -
with frequencies from about 1 GHz to 300 GHz, and wavelengths from 30 cm to 1 mm.
The most popular use of microwaves might be the microwave oven, which in fact
works in exactly the same region as the wireless standards we are dealing with.
These regions lie within the bands that are being kept open for general unlicensed
use. This region is called the ISM band, which stands for Industrial, Scientific,
and Medical.
Most other parts of the electromagnetic spectrum are tightly controlled by licensing
legislation, with license values being a huge economic factor. In many countries
the right to use portions of the spectrum have been sold to communications companies
for millions of dollars. In most countries, the ISM bands have been reserved for
unlicensed use and therefore do not have to be paid for when used.
The frequencies most interesting to us are 2.400 - 2.495 GHz, which is used by
the 802.11b and 802.11g standards (corresponding to wavelengths of about 12.5 cm),
and 5.150 - 5.850 GHz (corresponding to wavelengths of about 5 to 6 cm), used by
802.11a. The 802.11n standard can work in either of these bands.
See the Chapter called WiFi Family for an overview of standards and frequencies.
In addition you can find out more about the Radio portion of the electromagnetic
spectrum in the Chapter called Radio Spectrum.
Power
Any electromagnetic wave carries energy - we can feel that when we enjoy (or
suffer from) the warmth of the sun.
The amount of energy divided by the time during which we measure it is called
power. The power P is measured in W (watts) and is of key importance for a wireless
links to work: you need a certain minimum power in order for a receiver to make
sense of the signal.
We will come back to details of transmission power, losses, gains and radio sensitivity
in the chapter called Antennas/Transmission Lines.
Here we will briefly discuss how the power P is defined and measured. The electric
field is measured in V/m (potential difference per meter), the power contained within
it is proportional to the square of the electric field:
P ~ E2
Practically, we measure the power in watts by means of some form of receiver,
e.g. an antenna and a voltmeter, power meter, oscilloscope, spectrum analyzer or
even a radio card and laptop.
Looking at the signal's power directly means looking at the square of the signal
in volts and dividing by the electrical resistance.
Calculating with dB
By far the most important technique when calculating power is calculating with
decibels (dB). There is no new physics hidden in this - it is just a convenient
method which makes calculations a lot simpler.
The decibel is a dimensionless unit, that is, it defines a relationship between
two measurements of power. It is defined by:
dB = 10 * Log (P1 / P0)
...where P1 and P0 can be whatever two values you want to compare. Typically,
in our case, this will be some amount of power. Why are decibels so handy to use?
Many phenomena in nature happen to behave in a way we call exponential.
For example, the human ear senses a sound to be twice as loud as another one
if it has ten times the physical signal power.
Another example, quite close to our field of interest, is absorption. Suppose
a wall is in the path of our wireless link, and each meter of wall takes away half
of the available signal. The result would be:
0 meters = 1 (full signal)
1 meter = 1/2
2 meters = 1/4
3 meters = 1/8
4 meters = 1/16
n meters = 1/2n = 2-n
This is exponential behavior.
But once we have used the trick of applying the logarithm (log), things become
a lot easier: instead of taking a value to the n-th power, we just multiply by n.
Instead of multiplying values, we just add.
Here are some commonly used values that are important to remember:
+3 dB = double power
-3 dB = half the power
+10 dB = order of magnitude (10 times power)
-10 dB = one tenth power
In addition to dimensionless dB, there are a number of definitions that are based
on a certain base value P0. The most relevant ones for us are:
dBm relative to P0 = 1 mW
dBi relative to an ideal isotropic antenna
An isotropic antenna is a hypothetical antenna that evenly distributes power
in all directions.
It is approximated by a dipole, but a perfect isotropic antenna cannot be built
in reality. The isotropic model is useful for describing the relative power gain
of a real world antenna.
Another common (although less convenient) convention for expressing power is
in milliwatts. Here are equivalent power levels expressed in milliwatts and dBm:
1 mW = 0 dBm
2 mW = 3 dBm
100 mW = 20 dBm
1 W = 30 dBm































