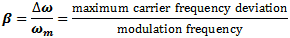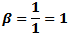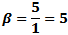|
 Frequency
modulation uses the instantaneous amplitude of a modulating signal (voice, music,
data, etc.) to directly vary the frequency of a carrier signal. Modulation index,
β, is used to describe the ratio of maximum frequency deviation of the carrier to
the maximum frequency deviation of the modulating signal. The concept was pioneered
by Edwin H. Armstrong in the late 1920s and patented in the early
1930s. Frequency
modulation uses the instantaneous amplitude of a modulating signal (voice, music,
data, etc.) to directly vary the frequency of a carrier signal. Modulation index,
β, is used to describe the ratio of maximum frequency deviation of the carrier to
the maximum frequency deviation of the modulating signal. The concept was pioneered
by Edwin H. Armstrong in the late 1920s and patented in the early
1930s.
Depending on the modulation index chosen, the carrier and certain sideband frequencies
may actually be suppressed. Zero crossings of the Bessel functions, Jn(β),
occur where the corresponding sideband, n, disappears for a given modulation index,
β. The composite spectrum for a single tone consists of lines at the carrier and
upper and lower sidebands (of opposite phase), with amplitudes determined by the
Bessel function values at those frequencies.
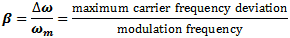
Narrowband FM is defined as the condition where β is small enough to make all
terms after the first two in the series expansion of the FM equation negligible.
Narrowband Approximation: β
= Δω/Ωm < 0.2 (could be as high as 0.5, though)
BW ~ 2ωm
Wideband FM is defined as when a significant number of sidebands have significant
amplitudes.
BW ~ 2Δω
J.R. Carson showed in the 1920's that a good approximation that for both very
small and very large β,
BW ~ 2 (Δω + Ωm)) = 2*Ωm (1 + β)
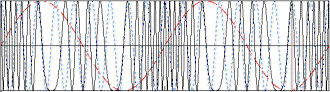
In the following examples, the carrier frequency is eleven time the modulation
frequency. Red (dashed) lines represent the modulation envelope. Blue (solid) lines
represent the modulated carrier.
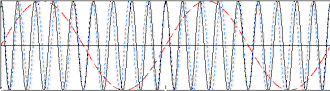
Here, the maximum frequency (fmax) causes a maximum deviation of 1*fmax
in the carrier. From the modulation index formula:
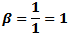
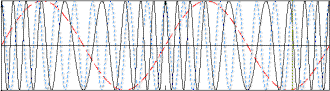
Here, the maximum frequency (fmax) causes a maximum deviation of 5*fmax
in the carrier. From the modulation index formula:
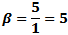
Here, the maximum frequency (fmax) causes a maximum deviation of 25*fmax
in the carrier. From the modulation index formula:
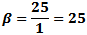
Note: FM waveforms created with MathCAD 4.0 software.
Technical Details
Frequency modulation (FM) is a widely used technique in RF communication, where
the frequency of a carrier wave is varied by a modulating signal to encode information.
A distinctive feature of FM is the behavior of its carrier amplitude, which can
be suppressed under specific conditions determined by the modulation index. This
suppression is mathematically tied to Bessel functions of the first kind, which
govern the spectral composition of an FM signal. Unlike amplitude modulation (AM),
where carrier suppression is achieved through external circuitry, FM carrier suppression
occurs naturally as a function of the modulation index. This treatise examines the
mechanisms of FM carrier suppression, its reliance on the modulation index, the
role of Bessel functions, and its implications for RF system design.
Fundamentals of Frequency Modulation
In FM, a carrier signal c(t) = Ac * cos(2 * π * fc * t)
with amplitude Ac and frequency fc is modulated by a signal
m(t) = Am * cos(2 * π * fm * t) with amplitude Am
and frequency fm. The instantaneous frequency deviates from fc
proportionally to m(t), resulting in:
sFM(t) = Ac * cos[2 * π * fc * t + β * sin(2
* π * fm * t)]
where β = Δf / fm is the modulation index, Δf = kf * Am
is the peak frequency deviation, and kf is the frequency deviation constant
(in Hz/V). The modulation index β quantifies the extent of frequency variation relative
to the modulating frequency, playing a central role in the FM spectrum and carrier
behavior.
Bessel Function Dependency
The FM signal's frequency spectrum is derived by expanding the phase-modulated
term using Bessel functions of the first kind. The expression becomes:
sFM(t) = Ac * Σ [n = -∞ to ∞] Jn(β) * cos[2
* π * (fc + n * fm) * t]
where Jn(β) is the Bessel function of the first kind, order n, with
argument β. The spectrum consists of:
- Carrier: Ac * J0(β) at fc (n = 0).
- Sidebands: Ac * Jn(β) at fc ± n * fm
(n = 1, 2, ...), appearing as infinite pairs symmetric around fc.
Key properties of Bessel functions relevant to FM include:
- J0(0) = 1, Jn(0) = 0 (n ≠ 0): At β = 0, only the carrier
exists.
- Jn(-β) = (-1)n * Jn(β): Symmetry ensures sideband
pairs balance.
- Σ [n = -∞ to ∞] Jn(β)2 = 1: Total power remains Ac2
/ 2, redistributing across components as β increases.
The carrier amplitude Ac * J0(β) varies with β, unlike
AM, where it is fixed unless externally suppressed. This variation enables natural
carrier suppression in FM, as detailed in the following table of Bessel function
values at key modulation indices where carrier and sideband nulls occur (color-coordinated):
| β |
J0(β) |
J1(β) |
J2(β) |
J3(β) |
J4(β) |
J5(β) |
| 2.4048 |
0.0000 |
0.5192 |
0.4318 |
0.1990 |
0.0647 |
0.0164 |
| 3.8317 |
-0.4028 |
0.0000 |
0.4028 |
4204 |
0.2556 |
0.1132 |
| 5.1356 |
-0.1323 |
-0.3397 |
0.0000 |
0.3397 |
0.3968 |
0.2785 |
| 5.5201 |
0.0000 |
-0.3403 |
-0.1233 |
0.2509 |
0.3960 |
0.3230 |
| 6.3802 |
0.2397 |
-0.1870 |
-0.2983 |
0.0000 |
0.2983 |
0.3740 |
| 7.5883 |
0.2534 |
0.1565 |
-0.2122 |
0.2684 |
0.0000 |
0.2684 |
| 7.0156 |
0.3001 |
0.0000 |
-0.3001 |
-0.1711 |
0.1538 |
0.3465 |
| 8.4172 |
0.0645 |
0.2714 |
0.0000 |
-0.2714 |
-0.1934 |
0.0875 |
| 8.6537 |
0.0000 |
0.2714 |
0.0627 |
-0.2425 |
-0.2308 |
0.0291 |
| 8.7715 |
-0.0317 |
0.2659 |
0.0923 |
-0.2238 |
-0.2454 |
0.0000 |
This table highlights carrier nulls (J0 = 0) at β
= 2.4048, 5.5201, and 8.6537, and first sideband nulls: J1 at 3.8317,
J2 at 5.1356, J3 at 6.3802, J4 at 7.5883, and J5
at 8.7715.
Carrier Suppression Mechanism
Carrier suppression in FM occurs when the carrier amplitude drops to zero, determined
solely by the modulation index β. The Bessel function J0(β,0) oscillates
and crosses zero at specific values; i.e., the carrier vanishes:
- First zero: β ≈ 2.4048
- Second zero: β ≈ 5.5201
- Third zero: β ≈ 8.6537
- Subsequent zeros follow at intervals of approximately
π (e.g., 11.7915, 14.9309).
The total power Ac2 / 2 redistributes to sidebands, with
higher-order terms (e.g., J3, J4) gaining prominence as β
increases. Unlike AM's DSB-SC, where suppression requires a balanced modulator,
FM achieves this intrinsically through β.
Modulation Index and Spectral Behavior
The modulation index β dictates the number and amplitude of significant sidebands:
- Narrowband FM (NBFM): β < 0.3
- J0(0.3) ≈ 0.978, J1(0.3) ≈ 0.148, J2(0.3) ≈
0.011 - mostly carrier, one sideband pair.
- Bandwidth ≈ 2 * fm, similar to AM.
- Wideband FM (WBFM): β > 1
- β = 5: J0(5) ≈ 0.1776, J1(5) ≈ 0.3276, J2(5)
≈ 0.0466 - multiple sidebands.
- Bandwidth ≈ 2 * (Δf + fm) (Carson's rule).
- Suppression Point: β = 2.4048
- Carrier null, sidebands carry all power.
As β rises, the spectrum widens, and the carrier's relative contribution diminishes,
hitting zero at Bessel nulls. This contrasts with AM, where sidebands scale linearly
with m, and carrier suppression requires external intervention.
Example 1: Narrowband FM Radio (Two-Way Communication)
A walkie-talkie operates at fc = 146 MHz, fm = 3 kHz (voice),
Δf = 0.9 kHz:
- β = Δf / fm = 0.9 / 3 = 0.3
- Spectrum:
- Carrier: Ac * J0(0.3) ≈ 0.989 * Ac
- Sidebands: fc ± 3 kHz, Ac * J1(0.3) ≈ 0.148
* Ac
- Higher orders negligible
- Bandwidth: 2 * (0.9 + 3) = 7.8 kHz
- Power: Carrier ≈ 97.8%, sidebands ≈ 2.2%
No suppression occurs - carrier dominates, keeping the signal compact for efficient
VHF comms.
Mathematical Analysis
Consider a practical example: fc = 100 MHz, fm = 5 kHz,
Δf = 12.024 kHz, so β = Δf / fm = 2.4048.
- Signal: sFM(t) = Ac * cos[2 *
π * 108 * t + 2.4048 * sin(2
* π * 5000 * t)]
- Spectrum:
- fc = 100 MHz: Ac * J0(2.4048) = 0
- fc ± 5 kHz: Ac * J1(2.4048) ≈ 0.5192 * Ac
- fc ± 10 kHz: Ac * J2(2.4048) ≈ 0.4318 * Ac
- Power: (0.51922 + 0.43182 + ...) * Ac2
= Ac2 / 2 (sum over all n)
The carrier vanishes, and energy redistributes, verifiable via Σ Jn(β)2
= 1.
Example 2: Wideband FM Broadcast with Suppression
An FM radio station at fc = 98.1 MHz, fm = 15 kHz (stereo
audio), Δf = 36.072 kHz:
- β = Δf / fm = 36.072 / 15 = 2.4048
- Spectrum:
- Carrier: Ac * J0(2.4048) = 0
- fc ± 15 kHz: Ac * J1(2.4048) ≈ 0.5192 * Ac
- fc ± 30 kHz: Ac * J2(2.4048) ≈ 0.4318 * Ac
- Up to J0(2.4048,5) ≈ 0.0164 * Ac
- Bandwidth: 2 * (36.072 + 15) ≈ 102 kHz
- Power: Carrier = 0%, sidebands = 100%
Full carrier suppression occurs—ideal for testing Bessel nulls, though broadcast
FM typically uses β ≈ 5 for richer audio.
Practical Implications
- Bandwidth Control
At β = 2.4048, bandwidth ≈ 2 * (12.024 + 5) = 34 kHz, wider than AM's 10 kHz
for the same fm. Higher β (e.g., 5.5201) increases bandwidth further,
complicating suppression via filtering. The following table illustrates this for
key suppression points:
| β |
Δf (kHz) |
fm (kHz) |
Bandwidth (kHz) |
Carrier Power (%) |
Sideband Power (%) |
| 2.4048 |
12.024 |
5 |
34.05 |
0.0 |
100.0 |
| 5.5201 |
27.601 |
5 |
65.20 |
0.0 |
100.0 |
| 8.6537 |
43.269 |
5 |
96.54 |
0.0 |
100.0 |
- Signal Design
Broadcast FM (e.g., Δf = 75 kHz, fm = 15 kHz, β = 5) rarely hits exact
nulls, but carrier weakening enhances sideband richness. Narrowband communications
(e.g., β = 0.5) avoid suppression for simplicity.
- Interference
Nulling the carrier at fc reduces interference with co-channel signals
but spreads energy, risking adjacent channel overlap.
- Detection
FM receivers (e.g., PLLs) extract m(t) from phase, not carrier amplitude - suppression
doesn't distort data, unlike AM.
Comparison to AM
- AM: Carrier suppression (DSB-SC) removes Ac * cos(2 *
π * fc * t) via multiplication,
leaving sidebands. Bessel zeros (e.g., J0(2.4048) = 0) apply only in
overmodulation analysis.
- FM: Suppression is inherent - no circuitry needed. J0(β) =
0 shifts power naturally, but sidebands can't be independently suppressed without
losing m(t).
FM carrier suppression is a direct consequence of the modulation index β and
its interaction with Bessel functions. At β values like 2.4048, 5.5201, and beyond,
J0(β) = 0, nulling the carrier and redistributing power to an expanding
array of sidebands. This natural phenomenon, rooted in the mathematics of Jn(β),
contrasts with AM's engineered suppression, offering unique advantages and challenges
in RF design. For engineers, understanding this dependency enables precise control
of FM spectra, balancing bandwidth, power distribution, and system performance in
applications from broadcasting to telemetry.
|