
Graph of P1dB, IP2, IP3, and Saturation
See also cascade calculations for NF, IP2, IP3, and P1dB.
When two or more tones are present in a nonlinear device, intermodulation products
are created as a result. A power series describes all of the possible combinations
of generated frequencies. 3rd-order products lie near in frequency to the two input
tones and are therefore very likely to fall inband at the output. As a device is
driven farther into its nonlinear region, the amplitudes of the third order products
increase while the powers of the input tones decrease. If the device was not limited
in output power, then the powers of the intermodulation products would increase
in power until they were eventually equal in power with the input tones at the output.
 Click here to view an example of a cascaded system.
Assuming a gain of 1 (0 dB) the slope of the fundamental gain line would be 1:1;
the slope of the 3rd-order gain line would be 3:1. Accordingly, the 3rd-order products
increase in power at twice the rate of the input tones and are always three times
farther away from the IP3 than the input tones when not near saturation.
The power of the 3rd-order products can be predicted when the IP3 is known, or
the IP3 can be predicted when the relative amplitudes of the 3rd-order tones and
the input tones are known.
Calculating the cascaded values for 3rd-order intercept point (IP3) for the system
budget requires use of ratios for gain and power levels for IP3 (do not use dB and
dBm values, respectively). The standard format for indicating decibel values
is to use upper case letters; i.e., IP3 for units of dBm. The standard format for
indicating power values is to use lower case letters; i.e., ip3 for units
of mW.
Conversions: ip3 = 10IP3/10 ↔
IP3 = 10 * log10 (ip3)
where ip3 has units of mW and IP3 has units of dBm
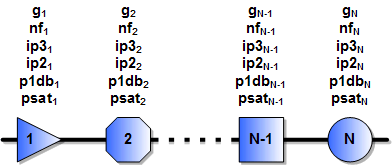
A Typical Chain of Cascaded Components

Combining 2 Stages at a Time for Calculations
This equation gives the method for calculating cascaded output
IP3 (oip3) values based on the oip3 and gain of each stage. When using the formula
in a software program or in a spreadsheet, it is more convenient and efficient to
calculate each successive cascaded stage with the one preceding it using the following
format, per the drawing (above-right). Note that the ip3N-1 term in
the denominator is the same as the cumulative ip3 up through the previous (N-1)
stage.


These formulas are used to convert back and forth between input- and output-referenced
IP3 values:
IP3Output = (IP3Input + Gain) {dBm}
IP3Input = (IP3Output - Gain) {dBm}
The following equation is a series expansion of the mixing (multiplying) of two
pure tones:

(see below for unequal powers)
P3rd-order products = Pinput tones@output
- 2 · (IP3 - Pinput tones@output) {dBm}
P3rd-order products = 3 · Pinput tones@output
- 2 · IP3 {dBm}
IP3 =3/2 · Pinput tones@output - 1/2 P3rd-order
products {dBm}
 PL
= P2 - 2*(IP3 - P1) PL
= P2 - 2*(IP3 - P1)
PU = P1 - 2*(IP3 - P2)
where power units are kept constant in dBm or dBW.
|










 PL
= P2 - 2*(IP3 - P1)
PL
= P2 - 2*(IP3 - P1)

