Introduction to Test Equipment
Navy Electricity and Electronics Training Series (NEETS)
Chapter 3:  Pages 3-1 through 3-10

Chapter 3

GYROS

Learning Objectives

Upon completion of this chapter you should be able to:

1.    Describe the characteristics of a gyroscopes.

2.    List the two basic properties of gyroscopes and explain them.

3.    Describe the components of a universally mounted gyro.

4.    Describe the factors that determine rigidity in a gyro.

5.    List the factors that determine the direction of precession in a gyro.

6.    Explain the right-hand rule for gyro precession.

7.    Describe the term "Degree of Freedom" as it applies to gyros.

8.    Explain the effect of apparent precession (apparent rotation).

9.    Explain the purposes of erection systems.

10.  Describe the use of gyros with only one degree of freedom.

11.  Explain the purpose of an accelerometer.

12.  Explain the principle on which accelerometers operate.

13.  Explain the need for a pulse-counting accelerometer.

GYROS

The word gyroscope was first coined by a French scientist, Leon Foucault, in 1852. It is derived from the Greek words "gyro," meaning revolution, and "skopien," meaning to view.

The gyroscope, commonly called a GYRO, has existed since the first electron was sent spinning on its axis. Electrons spin and show all the characteristics of a gyro; so does the Earth, which spins about its polar axis at over 1000 miles per hour at the Equator. The Earth's rotation about its axis provides the stabilizing effect that keeps the North Pole pointed within one degree of Polaris (the North Star).

Any rapidly spinning object - a top, a wheel, an airplane propeller, or a spinning projectile - is fundamentally a gyroscope. Strictly speaking, however, a gyroscope is a mechanical device containing a spinning mass that is universally mounted; that is, mounted so it can assume any position in space. Figure 3-1 shows a model of a gyro. As you can see, a heavy wheel (rotor) is mounted so that its spin axis is free to turn in any direction. The wheel spins about axis X; it can turn about axis Y, and it can turn about axis Z. With this mechanical arrangement, the spinning wheel can assume any position in space.

3-1

Figure 3-1. - Gyro model, universally mounted.

Basic PROPERTIES of GYROSCOPES

Gyroscopes have two basic properties: rigidity and precession. Those properties are defined as follows:

1.  RIGIDITY - The axis of rotation (spin axis) of the gyro wheel tends to remain in a fixed direction in space if no force is applied to it.

2.  PRECESSION - The axis of rotation has a tendency to turn at a right angle to the direction of an applied force.

The idea of maintaining a fixed direction in space is simple to illustrate. When any object is spinning rapidly, it tends to keep its axis pointed always in the same direction. a toy top is a good example. As long as the top is spinning fast, it stays balanced on its point. Because of this gyro action, the spinning top resists the tendency of gravity to change the direction of its axis. You can think of many more examples. a bicycle is easier to balance at high speed than when it is barely moving. At high speed, the bicycle wheels act as gyros, and tend to keep their axes (axles) parallel to the ground.

Note that it is easy to move the gyro as long as you keep the axis PointING in the SAME DirectION. The gyro resists only those forces that tend to change the direction of its axis. In a bicycle, since the axis of rotation (the wheel's axles) is horizontal, the wheels win resist any force that tends to tilt or turn them to the right or left.

If you can obtain a gyroscope top, you can do some instructive experiments with it. Hold the gyro top with its axis vertical as shown in figure 3-2 and start it spinning. As long as it is spinning fast, it will stay balanced. You can balance it on a string or on the point of your finger; the axis will stay vertical as long as the top is spinning fast. As we mentioned before, this ability of a gyro to keep its axis fixed in space is called RIGIDITY.

3-2

Figure 3-2. - a gyroscope top.

PRECESSION

Now, if you stop the gyro top and turn its axis horizontal, and then start it spinning again, balancing one end on a pivot, (fig. 3-3), it won't fall. The top's axis will stay horizontal, resisting the tendency of gravity to change its direction Although the gyro will RESIsT the force that gravity applies to it, the gyro will still RESPOND to that force. The gyro responds by moving its axis at a RIGHT ANGLE to the APPLIED forCE.

Figure 3-3. - Gyro top with axis horizontal.

The axis will tilt in a direction 90º away from the applied force. This is called PRECESSION.

Figure 3-4 is another view of the same gyroscope. Its far end is still balanced on the pivot. Gravity is pulling down on the gyro. If the gyro rotor is turning in the direction shown by the arrow, the near end of the frame (axis) will move to the left. If the rotor were turning in the opposite direction, the frame would move to the right. Note that in each of these examples the direction of movement was displaced from the applied force (gravity) by 90º. The axis stays horizontal, but the gyroscope responds to the force of gravity by rotating around the pivot.

3-3

Figure 3-4. - Gyro precession.

Gyro action may be summarized as follows: a spinning gyro tends to keep its axis pointing in the same direction. This is called RIGIDITY. If you apply a force that tends to change the direction of the spin axis, the axis will move at a right angle to the direction of the applied force. The direction of precession will be 90º clockwise from the applied force if the rotor is spinning clockwise (when viewed from the "free" end of the rotor's axis); if the rotor is spinning counterclockwise, the precession will be 90º counterclockwise. If the axis is horizontal, and you try to tilt it, the axis will turn. If the axis is horizontal, and you try to turn it, the axis will tilt. This second characteristic of a gyro is called

PRECESSION.

Because of precession, we can control the direction that the spin axis points. This enables us to aim the spin axis where we want it to point. Without precession, the rigidity of the gyro would be useless.

Q-1.   Can any rapidly spinning object be considered a gyroscope?

Q-2.   In the drawing in figure 3-1, which axis is the gyro spin axis?

Q-3.   What gyro property causes the gyro to remain in a fixed position?

Q-4.   What type(s) of force does a gyro resist?

Q-5.   In what direction will a gyro precess in response to an outside force?

Basic GYRO ELEMENTS

The gyro shown in figure 3-5 is a basic, universally mounted gyro, sometimes called a free gyro. Its components are rotor, inner gimbal, outer gimbal, and base or support. Gimbals are devices that permit the rotor to assume any position and retain that position when the support is tipped or repositioned. Note that in figure 3-5, the support may be moved about all axes without the rotor position being disturbed.

3-4

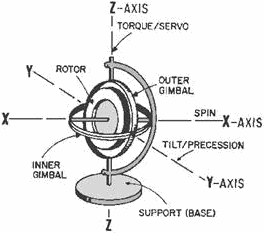
Figure 3-5. - Basic universally mounted gyro.

As you know, gravity is a force that acts along parallel lines upon each particle of matter. a plot of the resultant gravitational force on a body such as a gyro would be equivalent to the sum of these separate forces. The point at which the resultant force is applied is called the CENTER of GRAVITY. To have a balanced gyro, the center of gravity must be located at the intersection of the three axes of the gyro.

RIGIDITY

A gyroscope is a spinning body that tends to keep its spin axis rigidly pointed in a fixed direction in space. What do we mean by "fixed direction in space"? a fixed direction on Earth is by no means fixed in space, because the Earth turns once on its axis every 24 hours, and makes a complete revolution around the sun every year. The sun itself is moving through space, taking the Earth and the other planets with it. Because of these motions, the expression "fixed direction in space" as used in this explanation is theoretical. For all practical purposes, we can say a line from the Earth to a distant star is a fixed direction in space. If the spin axis of a spinning gyro is pointed at a distant star, it will remain pointed at the star as the Earth turns.

Gyro rigidity is the strength with which a gyro resists any external force that would tilt its rotor spin axis. There are three factors that determine gyro rigidity: weight of the rotor, distribution of this weight, and rotor speed.

The gyro can be considered as an enclosed mechanical system. The energy in the system is equal to the input energy. Hence the energy necessary to spin the gyro rotor is contained in the rotor as angular momentum, which is a function of rotor weight and the speed of rotor rotation. The heavier the gyro rotor, the larger the torque necessary to spin it, and the greater the angular momentum of the rotor. If we have two rotors with identical shapes but different weights spinning at the same velocity, the heavier of the two will be more rigid in its spin axis since it has the greater angular momentum.

3-5

Now let's look at the effect of weight distribution in the rotor of a gyro. Consider three rotors of the same weight, as shown in figure 3-6, view (A), view (B), and view (C), with the diameter of one rotor half the diameter of the other two. Now, when we spin these rotors at the same speed, we find that the rotors with the greater diameter are much more rigid than the one with the smaller diameter. Next, we find that we can make the rotors equally rigid by causing the rotor with the smaller diameter to spin faster than the larger rotors. Thus rigidity depends both on speed and distribution of weight. The weight of the larger rotor being farther away from the axis of spin causes it to be more rigid. This effect is even more pronounced if we shape the rotor as shown in view C of figure 3-6. Shifting as much weight as possible to the outer rim of the rotor increases rigidity even further.

Figure 3-6A. - Gyro rotors with equal weight and unequal diameters.

Figure 3-6B. - Gyro rotors with equal weight and unequal diameters.

Figure 3-6C. - Gyro rotors with equal weight and unequal diameters.

Q-6.   a universally mounted gyro has how many gimbals?

Q-7.   What factors determine the rigidity of a gyro?

3-6

Q-8.   Which gyro rotor in figure 3-6, view (A) view (B) view (C), will have the greatest rigidity if all are rotated at the same speed?

PRECESSION

To provide useful information, a gyro's spin axis must be related to some reference, usually the Earth's surface. This is done by using the second fundamental property of a gyro - PRECESSION. The gyro is precessed until its spin axis is pointed in the desired direction. So far we have covered precession in very general terms. The following paragraphs will cover this "gyro action" in more detail.

We can show precession by using the models in figure 3-7, view (A) and view (B). The gyro wheel is mounted so it is free to have its spin axis pointed in any direction. Here the wheel rotates in a flat loop called the gyro case (inner gimbal). The gyro case is pivoted in the gimbal ring (outer gimbal) and the gyro can swing about the Z axis. The gimbal ring itself turns on pivots that connect it to the fork (support). The fork permits the gyro to tilt from side to side about the Y axis.

Figure 3-7A. - Gyro action.

3-7

Figure 3-7B. - Gyro action.

Regardless of how the fork is placed, the spinning gyro wheel is free to lie in any given plane. That's why it is called a free gyroscope in this type of mounting.

To show the effect of precession, we can push down on the gimbal ring at point a at the nearer end of the Z-Z axis. (See view a of figure 3-7.) You might expect the ring to tilt around the Y-Y axis. Instead, the gyro case will tilt about the Z-Z axis. You can see the effect of this precession in view B.

Here's a rule that applies to all spinning gyros: The GYRO WILL ALWAYS PRECESS AT RIGHT ANGLES to The DirectION of The APPLIED forCE. Look at view a again. If we keep pushing down on the gimbal ring at point (A), the gyro case will keep turning until the spin axis of the gyro wheel is horizontal. Then there will be no further precession. At this point the gyro wheel will be spinning in the same direction in which the applied force is pushing.

Here's another rule: a GYRO ALWAYS PRECESSES IN a DirectION TENDING to LINE ITSELF UP SO THAT ITS ROTOR SPINS IN The SAME DirectION THAT The APPLIED forCE Is TRYING to Turn IT. In other words, the direction of spin chases the applied force. When the direction of spin and the applied force are in the same direction, precession stops.

Now, compare the spin (X) axis in the two parts of figure 3-7. In view A, the spin axis is vertical. In view B, the spin axis has moved from the vertical until it is much closer to being horizontal. By applying the right amount of force in the right place, we have a method of "aiming" the spin axis so that it points to the specific fixed direction in space where we want it. The property of PRECESSION makes the property of RIGIDITY useable.

You should understand that most forces, when applied to the gyro mounting, do not cause precession. For instance, you can swing the fork around in any direction, and the motion will merely be taken up in the Y-Y and Z-Z axes. Similarly, a force applied lengthwise along one of the axes will have no effect.

Any force acting through the center of gravity of the gyroscope does not change the angle of the plane of rotation but moves the gyroscope as a unit. The position of its spin axis in space is not changed. Such forces as those stated above, operating through the center of gravity, are forces of TRANSLATION. In other words, the spinning gyroscope may be moved freely in space by means of its supporting frame,

3-8

without disturbing the plane of rotation of the rotor. This condition exists because the force that is applied through the supporting frame, acting through the center of gravity produces no torque on the gyro rotor. ONLY THOSE forCES TENDING to TILT The GYRO WHEEL ITSELF WILL CAUSE PRECESSION.

Let's consider further the important characteristic of gyroscopic precession. For a given amount of force, the rate of precession of a gyro is governed by the weight, shape, and speed of the rotor. These factors are the same as those that determine the rigidity of a gyro. Therefore, there is a definite relationship between the rigidity of a gyro and the rate at which a given force will cause it to precess. The greater the rigidity of a gyro, the more difficult it is to cause precession, and the less precession there will be for a given force.

A gyro will resist any force that attempts to change the direction of its spin axis. However, it will move (precess) in response to such force; NOT in the direction of the applied force, but at right angles to it.

The direction a gyro will precess also depends on the direction the gyro is spinning. Precession is actually the result of two forces: angular momentum (spinning force) and the applied force (torque). The direction of precession is always offset from the direction of the applied force. The offset is always in the direction of rotor spin.

For example, when a force is applied upward on the inner gimbal, as shown in figure 3-8, the force may be visualized as applied in an arc about axis Y-Y. This applied force is opposed by the resistance of gyroscopic inertia, preventing the gyro from rotating about axis Y-Y. With the rotor spinning clockwise, the precession will take place 90º clockwise from the point of applied force. The gyro precesses about axis Z-Z in the direction of the arrow "P".

Figure 3-8. - Force applied to a gyro.

The motions of a gyroscope can be analyzed according to three basic quantities:

1.    SPIN (the angular velocity of the gyro rotor).

2.    TORQUE (the rotary motion applied to change the direction of the rotor axis).

3-9

3.    PRECESSION (the resulting angular change of the spin axis when torque is applied).

The above quantities are related to vectors so that the relative directions may be easily compared. The SPIN VECTOR lies along the spin axis of the rotor with an arrow indicating the direction of rotation. The TORQUE VECTOR represents the axis about which the applied force is felt. The PRECESSION

VECTOR represents the axis about which precession occurs. In all the above cases the direction of the vector is such that the quantity (spin, torque, or precession) is in a clockwise direction if viewed from the tail of the vector.

A simple hand rule will help you determine the direction of the SPIN VECTOR. (See fig. 3-9.) Curve the fingers of your fight hand in the direction in which the rotor is turning as if you intended to grasp the rotor. Your thumb will point in the direction of the spin vector. Similar rules will give you the direction of the TORQUE VECTOR and the PRECESSION VECTOR. With the fingers of your right hand wrapped in the direction of the applied torque (die direction the gyro would rotate if the rotor were not spinning), your thumb points in the direction of the torque vector. Placing your curved fingers in the direction of precession will place your thumb pointing in the direction of the precession vector.

Figure 3-9. - Determining spin vector direction.

All three motions are rotary (angular) and can be represented by vectors that point in such a direction that when you look in the direction of the vector the rotary motion around the vector is clockwise.

Another hand rule convenient for determining the DirectION of PRECESSION uses the fingers of the right hand. This method may not be new to you. a similar method is applied to electric motors (see NEETS, module 5).

You may represent the three vectors listed above by arranging the thumb, forefinger, and middle finger of your right hand mutually perpendicular as shown in figure 3-10. Your thumb points in the direction of the precession vector, your middle finger points in the direction of the torque vector, and your forefinger points in the direction of the spin vector. You can consider these vectors as the axes about which angular motion takes place. If you look in the directions your fingers and thumb point, you can visualize that all the rotary motions are clockwise as indicated in figure 3-10.

3-10