Coil-Winding Charts, August 1962 Electronics World

This is probably the handiest set of coil winding nomographs I have seen. Created by Donald Moffat, they appeared in the August 1962 issue of Electronics-World magazine. Sure, a calculator app might get the job done more quickly and to a greater number of decimal places, but the beauty of using the graphical approach is being able to get a mental picture of where all the numbers are in relation to each other. Besides, calculating a coil value to more than a couple significant digits is an exercise in vanity unless you are using a EM simulator where you are also defining dozens of physical parameters for the conductor, insulation, nearby structures, temperature, etc. The author explains how to use the dimensions of a coil to predict its inductance, distributed capacitance, and self-resonant frequency. With nomograms "calculations" are performed simply by drawing straight lines across the scales. Along with parameters like wire size, coil diameter and length, number of turns, and spacing (turns/inch), it also includes various types of insulation.

Fig. 1 - Basic coil geometry used in charts.

Inductance is only one of the characteristics that determines a coil's suitability in a specific application. Distributed capacity is equally important because it, along with inductance, determines self-resonant frequency of the coil, the point at which the coil becomes useless as an inductor. In fact, above its self-resonant frequency, any coil will act for all the world as if it were a poor capacitor, except that it will not block direct current.

This article will explain how to use the dimensions of a coil to predict its inductance, distributed capacity, and self-resonant frequency. Nomograms are included so that all "calculations" are performed simply by drawing straight lines across the scales.

Inductance is the property for which coils are used in circuits, and distributed capacity is another property we must take into account in order to know the useful inductance available. Roughly speaking, inductance can be increased by increasing either the diameter of a coil or its number of turns.

Increasing the number of turns is more effective because inductance increases as the square of the number of turns. In other words, doubling the number of turns will increase the inductance by a factor of four, tripling the number of turns will increase the inductance by a factor of nine. and so on. However, many of the changes made to increase inductance will also increase distributed capacity, and the over-all effect is to reduce the self-resonant frequency at a rapid rate. We can consider a practical coil as consisting of an ideal coil (pure inductance, and no capacity) in parallel with an ideal capacitor, and therefore increasing either one will reduce the resonant frequency according to f = 1/ (2π√LC). It is desirable, then, to have independent control over both inductance and distributed capacity. To a certain extent, such control is available to those who wind coils, through manipulation of the coil's silhouette. A series of 20-microhenry coils can be made, ranging from long and thin ones to short and fat ones. Although each coil has the same inductance, the different silhouettes will dictate that they have different values of distributed capacity and therefore different values of self-resonant frequency.

Dependence of distributed capacity on coil dimensions is not as straight-forward as inductance is, but there are a few general rules to serve as guides. Coils that range from short (those whose diameter is greater than the length) to medium (those whose length is two or three times the diameter) will just about double their distributed capacity when the diameter is doubled. In longer coils, up to those whose length is 50 times the diameter, there is very little dependence on diameter. Beyond that, we have the very long coils, where there is a definite reduction in distributed capacity as the diameter is increased.

The length of a coil has an effect on its value of distributed capacity, but the number of turns within a certain length has very little effect. For instance, a coil one-inch long could be wound with 24 turns of No, 18 wire, or it could be wound with 92 turns of No, 30 wire, but the distributed capacity will be about the same in both cases. This is a means of exercising separate control over inductance and capacity because you can take an existing coil design and switch to a finer size wire. This will allow you to put more turns in the same length, having little effect on distributed capacity but increasing inductance by the square of the added turns.

These statements will prove helpful as long as you realize that they apply only in a very general way and are on the lookout for exceptions. The nomograms will give numerical answers which are adjusted to take care of exceptions to these generalities.

Usually, the goal is to wind a coil with as little distributed capacity as possible. Even when a fair amount of capacity is acceptable, it should be controlled and its value known so that the coil will be compatible with the rest of the circuit. If minimum distributed capacity is the goal, the ideal coil is fatter than it is long, having a diameter about one and a quarter times its length. Unfortunately, this is not the most convenient shape to fit into an electronic chassis and it may be necessary to accept more than the minimum amount of capacity and arrive at a compromise coil shape. One advantage to the nomograms is that they make it easy to investigate various possibilities, as will be explained shortly.

Every coil must have some resistance, which will determine the "Q" factor. However, this factor determines just the sharpness of resonance and has very little bearing on the actual frequency of resonance. Since this article is restricted to an investigation of the interaction between inductance and distributed capacity, it will be assumed that the results are independent of coil resistance.

One of the most important factors in single-layer coils is the length-to-diameter ratio, which is used in the computations to follow. This ratio is found on Nomogram 1 and then is used as the first entry on the other two nomograms.

After the following instructions for using the nomograms, a simple numerical example will be presented.

Nomogram 1 - Chart used to find the length-to-diameter ratio and the distributed capacity of the air-core coils.

Distributed Capacity: Nomogram 1 is used for finding both the length-to-diameter ratio and the distributed capacity.

There are two sets of numbers along the first scale. Turns per inch, on the right-hand side of the scale is the basic number that is used for computations, and can always be used. The left-hand side of the scale, wire gauge, is for convenience in the unique but common case where single enamel wire is used and there is no spacing between turns. For any other situation, the graph, along with Fig. 2, can be used to arrive at a value of turns per inch. If the windings are closely spaced, follow the line for the type of insulation out to where it crosses the line for wire gauge and at that crossing note the number of turns per inch. For instance, the line for No. 36 wire crosses the line for single silk insulation at 150 turns per inch. If the turns are not wound as close as possible, but have some space between them, determine the values of D and S (see Fig. 1) and then on Fig. 2 follow that line out until it crosses the line for wire gauge, at which point you will read the turns per inch. Remember that S in the figure includes the insulation over the wire, a quantity that becomes increasingly important for fine wires.

Once turns per inch is determined, locate that value on the first scale of Nomogram 1, and the total number of turns on the second scale. Draw a straight line through these two points and extend it to cross the third scale, where you will read the length of winding. The actual value at this crossing is not important, as it is only the point of crossing that is going to be used for drawing the next line. On the other hand, if you knew the length of the coil, it would not be necessary to perform this first computation; simply locate that value on the length scale, and you are ready for the next step.

Next, locate the correct value on the diameter scale, and draw a straight line from that point to the indicated point on the length scale. Where that line crosses the middle scale, read a value of length/diameter, a value that will be used for each of the other computations. As with the length of the coil, this step does not have to be performed if the value is known, or if its computation can be done mentally. For instance, if your coil has a half-inch diameter and is one inch long, it is not necessary to draw the lines to determine that the ratio length/diameter is two.

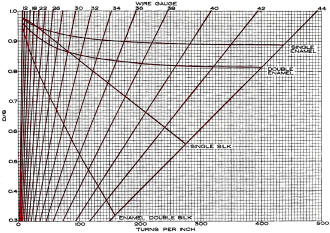
Fig. 2 - The number of turns per inch for wire having various types of insulation.

The last step in determining distributed capacity starts with locating, on the next to the last scale, the value which was found for length/diameter. Diameter has already been located on its scale. Draw a straight line through these two points and extend the line to cross the last scale. Now read the appropriate value of distributed capacity.

Notice the peculiar layout of the sixth scale, to which the value of length/diameter was transferred. Numbers go down from 50 to about 1 and then the rest of the scale, down to 0.1, is folded back on itself, so that some spots on the scale are used as the location of two numbers. Another point of interest is that numbers at the lower end of the scale are quite crowded together, meaning that any ratios in this range will give about the same amount of distributed capacity. Almost no accuracy would be lost by saying that any value of length/diameter between 1.2 and 0.6 is to be transferred to a location "near" the lower end of the scale.

Inductance: Once length/diameter has been determined from Nomogram 1, locate that value on the first scale of Nomogram 2, and locate number of turns on the second scale. Draw a straight line through these two points, extending it to cross the third scale. On the last scale, locate the correct value of the diameter. Then a straight line drawn from that point to the point where the first line crossed the turning scale will cross the fourth scale at the inductance of the coil.

One of the advantages to the use of nomograms can be illustrated at this time. If the inductance that is found is not the desired value, you can rotate a straight-edge about the crossing on the turning scale until it passes through the desired inductance. The straight-edge will then cross the diameter scale at the diameter necessary to give that inductance. You can then work the first nomogram backwards to find a new length of winding, and the coil is redesigned for the required inductance.

Self-resonant Frequency : Once length/ diameter has been determined from Nomogram 1, locate that value on the first scale of Nomogram 3, and locate the diameter on the second scale. Draw a straight line through these two points, extending it to cross the third scale. On the fourth scale, locate the correct number of turns, and draw a straight line through that point and the point where the first line crossed the turning scale. Extend that line to the last scale, where it will cross the self-resonant frequency for that coil.

Nomogram 2 - By using this chart, the inductance values of air-core coils of the sizes shown may be found.

Any coil is normally designed to operate at frequencies below self-resonance, where it has a useful inductance. At frequencies above self-resonance, nothing can be added to make the circuit resonate.

As with any other nomogram, it is easy to rotate a straight-edge about any point to see the effects of changing one or more of the numbers.

In order to be certain the instructions are clear, let's run through it again, with numbers. Suppose you have 140 turns of No. 32 enameled wire on a quarter-inch form. On Nomogram 1, locate 32 on the right-hand side of the first scale and 140 on the second scale. A straight line through these two points will cross the third scale at 1.25, the length of winding. Next, locate 0.25 (quarter inch) on the diameter scale and draw a line from that point to 1.25 on the length scale. It was not necessary to note that the length was 1.25 because that value is not used in any of the other computations and only the location of the crossing on that scale is important to further computations. A straight line drawn through these two points shows that the length/diameter ratio is 5. Locate 5 on the next to last scale and draw a line from 0.25 on the diameter scale, through 5 just located, and this line will cross the distributed capacity scale at 0.51 μμf.

Now, use Nomogram 2 to find the inductance. From 5 on its length/diameter scale, to 140 on its number of turns scale, draw a straight line and extend it to cross the turning scale. Draw another line from that crossing to 0.25 on the diameter scale and the answer of 22 microhenrys is found on the inductance scale.

Self-resonant frequency is found on Nomogram 3. Draw a straight line from 5 on the length/diameter scale to 0.25 on the diameter scale and extend it to cross the turning) scale. From that point of crossing on the turning scale, draw a line through 140 on the number of turns scale and extend it to cross the last scale. At that last crossing, read a self-resonant frequency of 48 megacycles.

Nomogram 3 - Chart employed to determine the self-resonant frequency of air-core coils from the number of turns and the size.

Several equations have been developed for computing the characteristics of a coil. Unfortunately, we do not have universal agreement on a single correct set of equations, each one seeming superior for different purposes. These nomograms have been based on equations that have been supported experimentally over the ranges of values used for the scales.

Coil leads, even though only a piece of straight wire, have both inductance and capacity that add to those of the coil proper. In fact, a straight piece of wire has a self-resonant frequency. For these nomograms, it has been assumed that there are no leads on the coil, an assumption that introduces negligible error until the coil is operating at frequencies of hundreds of megacycles and above. You can generally figure that the calculated value of self-resonant frequency is the maximum possible, and in the actual circuit, the coil will resonate at some lower frequency; some safety margin should always be allowed.

Usually, the number of turns cannot be determined precisely because the last turn does not have a definite ending, but tapers away from the rest of the winding. At least some part of the last turn (and of the first turn) is more of a lead than a part of the coil proper. Sometimes the last turn is wrapped around a terminal or a pigtail and soldered in place. Any wraps not shorted by solder will form another little coil, the characteristics of which will add to those of the main coil.

Weather conditions, such as temperature and humidity can have a noticeable effect on the characteristics of a coil, especially if sufficient and constant tension was not maintained during the winding.

Although the example used a quarter-inch coil form and we used 0.25 on the diameter scale, diameter is really meant to be taken to the center of the wire. For fine wire, the difference between the diameter of the coil form and the diameter to the center of the wire is too small to have any bearing on the answer. However, when using heavy wire on a coil form of small diameter, the accuracy can be improved by adding the diameter of the wire to the diameter of the coil form.

The nomograms have been based on air-core coils because the use of other material introduces several other variable conditions. Modifying the charts just to provide for the effects of slugs would complicate them to the point where their usefulness would be questionable. With air-core coils, however, considerable time and effort can be saved by using the charts.

Nomograms for determining the inductance, distributed capacitance, and the self-resonant frequency of coils.

Coil-Winding ChartsAugust 1962 Electronics World

Coil-Winding Charts
August 1962 Electronics World