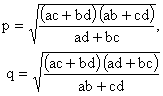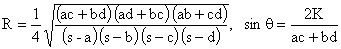Societal Influences
- See Full List of AI Topics -
A polygon is a two-dimensional
geometric figure that is formed by connecting a sequence of straight line segments
to create a closed shape. The segments are called sides, and the points where the
sides intersect are called vertices. Polygons can have any number of sides, but
they must have at least three sides.
The word "polygon" has its origins in the Greek words πολύς ("many") and γωνία
(gōnia), meaning "knee" or "angle."
Polygons are classified based on the number of sides they have:
Triangles: Triangles are polygons with three sides and three vertices. They are
further classified into:
Equilateral triangle: All three sides are equal in length. Isosceles triangle:
Two sides are equal in length. Scalene triangle: All three sides have different
lengths. Right triangle: One angle is a right angle (90 degrees). Quadrilaterals:
Quadrilaterals are polygons with four sides and four vertices. They include:
Square: All four sides are equal in length, and all angles are right angles.
Rectangle: Opposite sides are equal in length, and all angles are right angles.
Parallelogram: Opposite sides are parallel and equal in length. Rhombus: All sides
are equal in length. Trapezoid (or trapezium): One pair of opposite sides is parallel.
Pentagons: Pentagons have five sides and five vertices.
Hexagons: Hexagons have six sides and six vertices.
Heptagons: Heptagons have seven sides and seven vertices.
Octagons: Octagons have eight sides and eight vertices.
And so on...
Polygons can also be classified as regular or irregular. Regular polygons have
all sides and angles equal in measure, while irregular polygons have sides and/or
angles of different lengths or measures.
The sum of the interior angles of any polygon can be found using the formula:
(n-2) * 180 degrees, where n is the number of sides.
This content was generated by the ChatGPT
artificial intelligence (AI) engine. Some review was performed to help detect and
correct any inaccuracies; however, you are encouraged to verify the information
yourself if it will be used for critical applications. In some cases, multiple solicitations
to ChatGPT were used to assimilate final content. Images and external hyperlinks
have also been added occasionally. Courts have ruled that AI-generated content is
not subject to copyright restrictions, but since I modify them, everything here
is protected by RF Cafe copyright. Your use of this data implies an agreement to
hold totally harmless Kirt Blattenberger, RF Cafe, and any and all of its assigns.
Thank you. Here are the major categories.
Electronics & High Tech
Companies | Electronics &
Tech Publications | Electronics &
Tech Pioneers | Electronics &
Tech Principles |
Tech Standards
Groups & Industry Associations |
Societal Influences on Technology
|



























 (Pythagorean)
(Pythagorean)









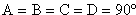










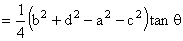
 (Bretschneider's Formula)
(Bretschneider's Formula)

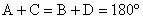

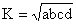






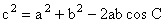 (Law of Cosines)
(Law of Cosines)
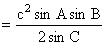

 (Heron's formula)
(Heron's formula)
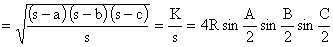
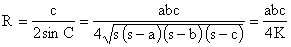





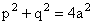


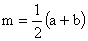


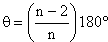


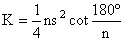

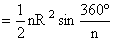


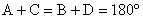
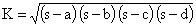 (Brahmagupta's
formula)
(Brahmagupta's
formula)