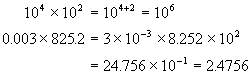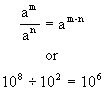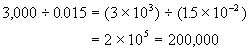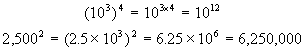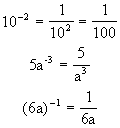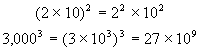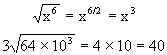Custom Search
Over 10,000 pages indexed!
|
| Your Host |
 KirtBlattenberger ... single-handedly redefining what an engineering website should be.
5CCG (5th
MOB): |
|
Hobby & Fun Airplanes and Rockets: Equine Kingdom: Doggy Dynasty: |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Navy Electricity and Electronics Training Series (NEETS) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Module 1—Introduction to Matter, Energy, and Direct Current
Pages i - ix, 1-1 to 1-10, 1-11 to 1-20, 1-21 to 1-30, 1-41 to 1-50, 1-51 to 1-60, 1-61 to 1-65, 2-1 to 2-10, 2-11 to 2-20, 2-21 to 2-29, 3-1 to 3-10, 3-11 to 3-20, 3-21 to 3-30, 3-31 to 3-40, 3-41 to 3-50, 3-51 to 3-60, 3-61 to 3-70, 3-71 to 3-80, 3-81 to 3-90, 3-91 to 3-100, 3-101 to 110, 3-111 to 3-120, 3-121 to 3-126, Appendix I, II, III, IV, V, Index
APPENDIX II LAWS OF EXPONENTS The International Symbols Committee has adopted prefixes for denoting decimal multiples of units. The National Bureau of Standards has followed the recommendations of this committee, and has adopted the following list of prefixes:
To multiply like (with same base) exponential quantities, add the exponents. In the language of algebra the rule is am x an = am+n
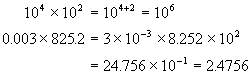
AII-1 To divide exponential quantities, subtract the exponents. In the language of algebra the rule is
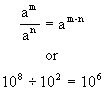
*Generally used with electrical quantities.
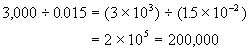
To raise an exponential quantity to a power, multiply the exponents. In the language of algebra (xm)n = xmn.
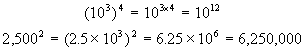
Any number (except zero) raised to the zero power is one. In the language of algebra xO = 1
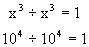
Any base with a negative exponent is equal to 1 divided by the base with an equal positive exponent. In the language of algebra x-a = 1/xa
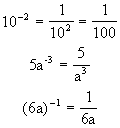
To raise a product to a power, raise each factor of the product to that power.
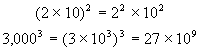
AII-2 To find the nth root of an exponential quantity, divide the exponent by the index of the root. Thus, the nth root of am = am/n.
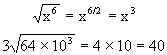
AII-3
Introduction to Matter, Energy, and Direct Current, Introduction
to Alternating Current and Transformers, Introduction to Circuit Protection,
Control, and Measurement, Introduction to Electrical Conductors, Wiring Techniques,
and Schematic Reading, Introduction to Generators and Motors,
Introduction to Electronic Emission, Tubes, and Power Supplies,
Introduction to Solid-State Devices and Power Supplies,
Introduction to Amplifiers, Introduction to
Wave-Generation and Wave-Shaping Circuits, Introduction to Wave Propagation, Transmission
Lines, and Antennas, Microwave Principles,
Modulation Principles, Introduction to Number Systems and Logic Circuits, Introduction
to Microelectronics, Principles of Synchros, Servos, and Gyros,
Introduction to Test Equipment, Radio-Frequency
Communications Principles, Radar Principles, The Technician's Handbook,
Master Glossary, Test Methods and Practices, Introduction to Digital Computers,
Magnetic Recording, Introduction to Fiber Optics
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
