 [Index] [Index]
Reproduced here are various Mathematical Puzzles from
The Old Farmer's Almanac,
published continuously since 1792. All copyrights hereby acknowledged.
|
Here is another set of "Old and New Mathematical Puzzles,"
compliments of the 1985 edition of the Old Farmer's Almanac. All of the
puzzles from Difficulty 1 through Difficulty 3 can be worked out without much
trouble. Puzzle number 3 is a variation on an optical illusion based on the
Möbius strip, or maybe
more like a Klein bottle.
Of course, being a farmer thing, there's a puzzle involving the number and price
of produce at the market. There are four Difficulty 5 puzzles for which no
solutions are given. They are the ones where readers are invited to submit
solutions, and the winner for each receives a $50 award and honorable mention in
the next year's edition. The winning solutions are never shown, but you can
write to request a copy of them. It would be interesting to see what the
solutions look like for this year's puzzle 13. You need to be good at
three-dimensional drawing to render them.
Old and New Mathematical Puzzles
Blanton C. Wiggin, Puzzle Editor
From many puzzles submitted by readers we have selected 15 classical, original,
or timely puzzles for 1985. They are graded for difficulty, so that there should
be something of interest for everyone. We hope you find them challenging. No calculus,
computers, or tricks. We try to include specialized knowledge, if needed, in the
puzzle statement.
We will award one prize of $50 for the best set of solutions to puzzles 12 through
15 received before February 1, 1985. The answers to these four are omitted here.
These may sometimes require a chart or table of data from your local library.
We use a point system to judge the prize set. A basic, unadorned, correct answer
is 20 points. For a thorough analysis, an elegant or novel answer, up to 5 points
extra. Numerical errors lose only 2 or 3 points, if it is clear that the method
is understood.
Explanations and Prize-Set Answers will be mailed after June 1 to anyone sending
50¢ and a self-addressed, stamped envelope to "Puzzle Answers," The Old Farmer's
Almanac, Dublin, NH 03444.
We'll also pay $15 for any original puzzles we use in The Old Farmer's Almanac
for 1986. Closing date for submissions is March 1, 1985. Entries become the property
of Yankee Publishing Incorporated and cannot be acknowledged or returned. In addition
to submitting a puzzle, please tell us the type of puzzle you like best, such as
magic squares, geometry, time-rate-quantity, mazes, logic, number substitutions,
etc.
From a group of good answers, we are happy to announce a first-time winner for
1984: Leon Kreidler, Sheboygan, Wis., with 88 points; followed by Walter Beveridge,
Hartsdale, N.Y., 86; and past winner Newton Amos, St. Louis, Mo., 81. Other high
scorers were Paul Nektaredes, Tarpon Springs, Fla., and Douglas J. Madea, Manheim,
Pa.
Please submit your favorite puzzles and send your answers early for puzzles 12-15.
Use a separate sheet for each puzzle or answer, and be sure each sheet has your
name and address on it. Good luck!
Answers appear on page 200.
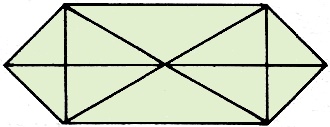 1. Russian Markets 1. Russian Markets
Difficulty: 1
a. Carpenter Hammer charged Farmer Sickle a capitalistic 5 rubles to saw a board
into 2 pieces. At that rate, what should he charge to make 4 pieces?
b. Sickle then challenged Hammer double or nothing to plow this pattern with
one continuous line, never crossing itself. Did Sickle pay?
Matt McCullar
Fort Worth, Texas
2. Telling Time
Difficulty: I
a. In England and some other countries 9-2-85 usually means February 9. In the
U.S., most people think of September 2. During a year, how many dates can be confused?
b. During a single day, from one midnight to the next, how many times is the
minute hand on a clock lined up with the hour hand?
Paul R. Erickson
Frankfort, Ill.
3. This and That
Difficulty: 2
This and That are whole numbers. This and That, plus 1/2 of This, and That again
= 11. How much is This and how much is That?
Walter I. Christopher
Carmichaels, Pa.
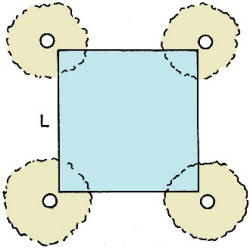 4. Enlarged Pool 4. Enlarged Pool
Difficulty: 2
Mr. Jones owns a square pool with a tree at each corner. He has decided to enlarge
the pool, but being a lover of nature, he wants to save his trees. The pool must
maintain its original shape, and no tree is to be moved or cut down.
Suppose a side of the original pool is L. What is the maximum area of the enlarged
pool?
Jose Diaz
Boston, Mass.
5. Short-Cut Math
Difficulty: 2
Quite obviously 26/65 = 2/5 by canceling the sixes! What other fractions with
denominators less than 100 reduce correctly by incorrect means?
Anita Burpee
Goffstown, N.H.
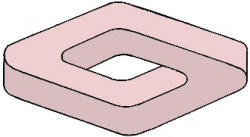 6. Double Vision 6. Double Vision
Difficulty: 3
a. If this three-dimensional object were constructed correctly, it would have
four outside surfaces. However, someone goofed! How many outside surfaces does this
"thing" have?
b. If the object were a true conventional picture frame instead, 1" wide, what
size picture, in whole inches on each side, would have an area equal to the face
area of the frame?
M.A. Frost
Fort Worth, Texas
7. Peas, Beans & Barley
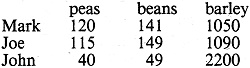 Difficulty: 3 Difficulty: 3
a. Mark, Joe, and John, all farmers, went to the market one day to sell their
produce. They offered the following bushels:
If the peas sell for $5 a bushel and beans for $4, how much would the barley
price have to be for John to receive more money for all his produce than Joe and
Mark put together?
b. Feeling flush, John then bought some additional farm land for $10,000. Next
day he felt differently and resold it for $10,200, but decided almost immediately
that it was undervalued, He prevailed on his customer to sell back to him for $10,300
and sold it to someone else for $10,600 the third day.
How much did John gain or lose?
Eric Burgess
Greenwood, Tenn.
8. The One That Got Away
Difficulty: 3
We know that
- Fishermen tell tall tales.
- A flytier once said, "All flytiers are liars."
- No flytier is both honest and a liar.
Therefore, is the flytier a truth-teller feller or a tall-tale teller? Or are
the facts contradictory?
V. V. Lloyd
Lynchburg, Va.
9. Espionage Express
Difficulty: 4
Four spies in trench coats sat in two facing bench seats as they rode the Orient
Express. Two sat next to the window and two next to the aisle. The English spy sat
on Mr. B's left. Mr. A wore a tan-colored coat. The spy in olive was on the German
spy's right. Mr. C was the only cigar-smoker. Mr. D was across from the American
spy. The Russian was in khaki and the English spy stared out the window on his left.
Who was the spy in the rust-colored coat?
Paula Reiter
Midwest City, Okla.
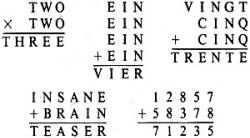 10. Deux and Zwei 10. Deux and Zwei
Difficulty: 4
Can you substitute the same number for a letter each time the letter appears
(or for a different digit in the last sum), for mathematically correct answers?
Each problem is different, and there may be more than one answer to some.
No left-hand zeros, please.
11. Endings
Difficulty: 4
a. What are the last three digits of 19851985?
b. What are the last three digits of 79999?
c. For what n is this true? 1324n + 731n = 1961n?
Gary Gettel
Plano, Texas
12: Diagramless Cross-number
Difficulty: 5
Across or Down
- The year of-this OFA.
- The sum of the six numbers in the puzzle is a perfect square.
- No number in this puzzle begins with zero, of course.
- Each of the ten digits is used only once in this puzzle.
- Only one of the six numbers is composite.
- Sorry you don't get a diagram or numbers, but if you make the first clue above
go across, the solution is probably unique.
Bob Lodge
Seattle, Wash.
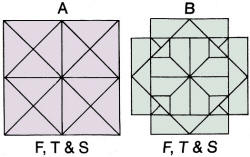 13. Look Alikes 13. Look Alikes
Difficulty: 5
Here are 2 solid objects, a and b. The front, top, and side views of each are
all the same.
Can you draw a perspective or describe each? No wire, sheet metal, or surface
designs. Some solid lines may hide dashed lines as is customary in mechanical drawing,
but there are no unshown purely dashed lines.
A. W. Mosenthal
Corinth, Vermont
14. Big Number
Difficulty: 5
What is special about: 8,589,869,056?
David Edgar
Hartford, Conn.
15. Curious Cubes
Difficulty: 5
a. How many unique ways can you arrange 5 equal cubes so that at least one face
of each cube fully touches another cube? Partial, edge, and corner touching don't
qualify. Simple rotations are not unique; mirror arrangements that cannot be rotated
are.
b. If the cubes are dice, what is the maximum outside score that can be shown
on an arrangement?
c. What is the maximum number of equal cubes whose faces can simultaneously touch
the faces of a single cube of the same size? Partial touching OK; edges and corners
not.
Fred Richardson
Lincoln, Mass.
***
Answers
 1. a. If stacked, R10; otherwise, R15. 1. a. If stacked, R10; otherwise, R15.
b. Sickle paid double:
2. a. 11 a month or 132.
b.23.
3. 6 & 1, or 2 & 4.
4. 2L2
5. 19/95, 16/64, 49/98, 46/69 = 64/96 and others
6. a. 2.
b. 3" X 10", or 4" x 6".
7. a. $32.317/bu
b. $500 gain
8. Liar. If he were truthful, his statement would be incorrect. If a liar, the
facts are possible.
9. The Englishman, Mr. D.
10.
11. a. 625
b. 143
c. None. This is an example of Fermat's unproven Last Theorem. In this case,
note the right-hand digits.
12-15: Prize set. See instructions, page 192.
Posted February 27, 2024
|








 1. Russian Markets
1. Russian Markets 

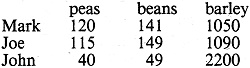 Difficulty: 3
Difficulty: 3 


