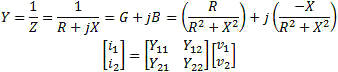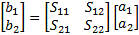|
Sunshine Design Engineering Services
See list of all of Joe's articles at bottom of page.
Scattered Thoughts on Scattering Parameters
By Joseph L. Cahak Copyright 2013 Sunshine Design Engineering Services
Scattering parameters or S-parameters (aka Spars) are used by RF and microwave
engineers to measure and design components and systems at those frequency ranges.
These S-parameters are typically measured with an instrument called a vector
network analyzer, or VNA.
Complex Numbers and Parameters
A complex number is represented by two values X and Y, as in X + iY = Z.
X is the real component and iY is the imaginary component with Z being the complex
representation. The letter ‘i' is used to designate the complex operator (√-1)
by scientists and mathematicians, but in engineering the letter ‘j' is most
often used. This is used to represent AC or RF signals. X may be the resistance
and Y the reactance in ohms of the component to an AC signal. A standard RF
load for instance is represented by 50 ohms real resistance and some reactance
with good loads having reactance close to 0 ohms. X + iY can also
represent a voltage and current as a function of time. Current is a function
of the load and the voltage applied, so the resistances, voltages and currents
are all important in describing a network for DC and AC (or RF) signals. A 2-port
network can be represented by two equations with four parameters. The four parameters
have different representations depending on what is known and what operations
the users desire to use them for. Some network parameters (ABDC, S-, Z-, Y-,
h-, etc.) are better than others depending on circuit types and the operations
on them.
Z Parameters
Open circuit impedance parameters are used to represent the impedances of
the network. The values are complex and represent real resistance (R) and reactance
(jX) of the elements of the network.

Y Parameters
Short circuit parameters or admittance parameters are used to represent the
inverse of impedance. The real and imaginary parts are conductance (G) and susceptance
(jB). The units are mhos or Siemens.
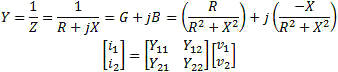
h Parameters
Another model commonly used to analyze BJT (bipolar junction transistor)
circuits is the h-parameter model, closely related to the hybrid-pi model and
the y-parameter two-port model, but the h-parameter model uses input current
and output voltage as independent variables, rather than input and output voltages.
In this case it is a hybrid of an open circuit on the input and a short circuit
on the output.

g Parameters
Often this circuit is selected when a voltage amplifier is wanted at the
output. The off-diagonal g-parameters are dimensionless, while diagonal members
have dimensions the reciprocal of one another.

ABCD or T Parameters
ABCD-parameters are known variously as chain, cascade, or transmission line
parameters. This is useful for cascading 2 port network responses.

ABCD' or T' Parameters
These are the inverse of the ABCD or T-parameters, respectively. They are
useful for de-embedding 2-port network responses when multiplied with the ABCD
matrix for the overall network.

Network Transforms
There are matrix transforms that are used to convert from one network description
to another. Typically the S, Z, Y, h and ABCD are direct conversions. The conversion
to a few of the others are after the base conversion and then converting from
h to the inverse g for instance, ABCD with the inverse ABCD-1 and S-parameter
to the T (one of the two types) or the anti-S parameter (S-1) . Note
that the ABCD matrix is also known as a “T” matrix; this is not to be confused
with the other two descriptions of a “T” matrix connected with the S-parameters
calculations and will be presented in another paper. See Figure 1 for a graphical
representation of the transformations available.

Figure 1 - Network Description Transformations
Transmission Lines
Some of the transmission line functions and parameters are complex in value.
They are excited by RF signals with most having complex modulation applied to
them. Some basic measurement parameters need to be defined. A load can be represented
at RF frequencies as a real resistance and an imaginary reactance driven by
the charge delay or advancement as related to the driving voltage. This complex
impedance is written as Z(ohms) = X + iY, with Z being complex
value of the real (X) and imaginary (Y) components. Y is positive for an inductive
element and negative for a capacitive element.
Reflections
When a RF signal is incident to a load, some of the signal is absorbed and
converted to heat and radiated, what isn't absorbed is reflected back to the
source as shown in Figure 2 and 3. Reflection coefficient represents this value
in power measurements and is also known as rho or
ρ = Γ = |Power Reflected/Power Incident|.
Rho can be converted to the voltage standing wave ratio, or VSWR, by the equation
VSWR = (1+ρ)/(1-ρ). These measurements
are still scalar, but dimensionless. Rho and VSWR are measured in units of power
(single dimension), but the ratio cancels the units out (thus dimensionless).
Rho and VSWR can also be derived by the system impedances. The load can be represented
by Z = R +jX. The measurement system used to characterize a component
or another system also has impedance. This measurement with the device or network
sets up an impedance match represented by gamma or Γ = (Zsys-Z)/(Zsys+Z)
= (Power Reflected)/(Power Incident). The gamma, or complex reflection
coefficient, can be transformed by absolute value to rho, or
ρ=|Γ| , which can
be used to derive the VSWR as given above. It can also be transformed by the
system impedance to the load impedance.


Figure 2 – S11 or Gamma Source Signal Flow

Figure 3 - Power Reflected
Transmission
When a signal is incident to a 2-port network, the network looks like a load
to the source, but the network has an output and a match at the output. The
device has reflections from the output back to the input in addition to the
transmitted part of the incident signal. As with the Reflection case, there
is also some energy absorbed and converted to heat. The transmitted signal can
be represented by Tau or
τ = (Power Transmitted)/(Power Incident).
See Figures 4 and 5.

Figure 4 - Transmission Network Signal Flow

Figure 5 - Transmitted Power
Units of Measurement
Resistance is measured in ohms, voltage in volts, current in amps. Power
is measured in watts. This can be referenced to a specific power level. Tradition
and convention stipulate 1mW as 0 dBm. With this power can be represented
in logarithmic units or decibels, dB for relative power gain or loss and dBm
for absolute power level referenced to 1 mW. When power is measured the
type of measurement makes a difference in how the units are converted. A Power
Meter measures in Volt-Amps or true power as opposed to reactive or apparent
power. The formula to convert real power to decibels is
dB = 10*log10 [(Power Out)/(Power In)].
To convert measurements made in voltages, not true power, and this includes
vector network analyzers, vector signal analyzers and spectrum Analyzers use
the formula
dB = 20*log10 [(Voltage Out)/(Voltage In)].
This can be derived from the fact that Power = Voltage2/Resistance
, thus the doubling of the multiplier of the logarithm of the voltage ratio
measurement of power. Convert dB to Watts using the inverse formulas:
Watts = 10Power/10 and Watts=10Voltage20
.
The absolute power can be converted between Watts and dBm with the following
equations:
Watts =10 (dBm/10) - 3 and dBm = 10*log10
(Watts*1000)
dB units is a relative or ratio measurement. For power measurements adopted
convention is to measure the signal relative to 1 mWatt for dBm and 1 V
for dBV.
S-Parameter Definitions
S-parameters a and b components are in units of power represented as the
square root of the power or
Power Incident at Port 1 or a1 = V1+/√Zo
Power Incident at Port 2 or a2 = V2+/√Zo
Power Emitted at Port 1 or b1 = V1-/√Zo
Power Emitted at Port 2 or b1 = V2-/√Zo
b1 = S11a1 + S12a2
b2 = S21a1 + S22a2
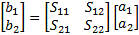

Figure 6 - 2-Port S-Parameter Signal Flow
Figure 6 shows the signal flow diagram for the S-Parameters. Note that the
dimension of a1,a2 and b1,b2 are
complex. These can then be used to derive the Scattering Parameters (Spars)
for the network which are also complex values and dimensionless due to the ratio
and in the case below are in rectangular coordinates and have linear magnitudes,
not dB. Note that S-Parameters are dependent on the system Impedance. S-Parameters
at one system impedance are not equal to S-Parameters at another System Impedance.
S11 = b1/a1 or forward reflection
coefficient S12 = b1/a2 or
reverse transmission coefficient S21 = b2/a1 or
forward transmission coefficient S22 = b2/a2 or
reverse reflection coefficient
Note also that the reflection coefficient for the load and source,
ΓL = b2/a2 and
Γs = b1/a1
, respectively are the same as S22 = b2/a2 and
S11 = b1/a1 . In other
words, if you measure the 1 port S-Parameter of a source or load, it is the
same as the Gamma or
Γ . These
S-parameters are the basis of many RF and Microwave measurements.
Network Analyzer Measurements
In many RF and Microwave measurements the S-Parameters are typically expressed
in dB (decibels) Magnitude units and Degrees in the polar coordinate system.
Network and Vector Network Analyzers and Spectrum Analyzers all measure with
voltage ratio measurements, so to convert to dB in terms of volts we must use
the following equation.
dB = 20*log10 [(Voltage Out)/(Voltage In)]
Making measurements of S-parameters is a process of measurements made with
calibrations standards (special components with values traceable to NIST or
other designated agencies) and formulas to compute the correction factors from
the measurement of those standards that determine a reference plane for the
measurements. The measurement reference plane is an imaginary plane of reference
for the measurements being made that lies somewhere between the measurement
system's output and input ports, inclusive. It defines the points to which the
network analyzer is calibrated to have 0 dB magnitude and 0 degrees phase
response. It is the input and output planes to which reflection and transmission
measurements are referenced. Another aspect of the relative measurement is that
within the VNA dynamic range, the input power can be varied and the network
response will stay the same until the power level goes outside the dynamic range.
There are numerous methods and standards for coaxial, waveguide, planar,
probe and other interconnections methods. There are also a number of test fixtures
available and calibration techniques to help the test engineer make measurement
in fixtures and give them the ability to de-embed fixture components to get
at the raw device or subsystem S-parameters, which are difficult or nearly impossible
to measure with standard equipment (e.g. mixed impedances).
New Stuff
I recently attended the Agilent “Back to Basics” seminar and as with the
first one I attended 20 years ago, they still cover all the basics of measurements,
S-parameters, measurement systems and how to use them. The new instruments all
have the extended measurement capabilities built in with some really exciting
capabilities. Spectrum analyzers can now reach down into the noise floor “Noise
Floor Extension” and get to -172 dBm/Hz. This is a mere 2 dB from
the theoretical noise limit at room temperature (recall that 25°C gives a 50 ohm
noise power of -174 dBm in a 1 Hz bandwidth).
The new oscilloscopes have some amazing features across the board and at
lower costs. They have very high bit depth and are being used for the spectrum
analyzer and vector signal analyzers (VSA) front ends, as they have in some
cases more than 14 bits of ADC depth, thereby giving much greater dynamic range.
Finally the exciting news on the vector network analyzer (VNA) measurement front
is the new X-parameter test sets that can do large signal multi-harmonic, power
and spurious analysis, in addition to the small signal S-parameters. This is
important because now the non-linear characteristics of device and circuit response
can be measured in addition to the linear characteristics. With this new information
much more accurate device and circuit models can be formulated, yielding a more
accurate model for designers to use in simulations.
Conclusion
We showed that S-parameters can be used for a number of network computations
that can add value to measurements where the equipment is limited in features.
The reader can find these equations and more in my S-Parameter Library (DLL &
LLB) and my RF Calculator products.
References
www.AstroCalculator.com
See RF Calculator and soon Labview S-Parameter Library
https://en.wikipedia.org/wiki/Two-port_network
https://en.wikipedia.org/wiki/S-parameters
https://en.wikipedia.org/wiki/ABCD-parameters#ABCD-parameters
https://en.wikipedia.org/wiki/Transmission_line
https://en.wikipedia.org/wiki/Reflection_coefficient
https://en.wikipedia.org/wiki/Standing_wave_ratio
https://en.wikipedia.org/wiki/Electrical_impedance
https://en.wikipedia.org/wiki/Admittance
https://en.wikipedia.org/wiki/Two-port_network#Hybrid_parameters_.28h-parameters.29
https://en.wikipedia.org/wiki/X-parameters
LinkedIn: Joe Cahak
Making S-Parameter measurements in Mixed Impedances, Jim Hillstrom, Microwaves &
RF, January 1992
Agilent PN 8720-2, In-fixture Microstrip Device Measurements
Using TRL* Calibration, Product Note
Agilent PN 8510-5A, Specifying Calibration Standards for the Agilent 8510
Agilent 8510-13, Measuring Noninsertable Devices, Product Note
Agilent AN 1287-1, Understanding the Fundamental Principles of Vector Network
Analysis, Application Note
Agilent AN 1287-3, Applying Error Correction to Network Analyzer Measurements,
Application Note
Agilent Application Note 1287-7, Improving Network Analyzer Measurements
of Frequency-translating Devices
Agilent AN 1287-6, Using a Network Analyzer to Characterize High-Power Components,
Application Note
Agilent AN 1287-9, In-Fixture Measurements Using Vector Network Analyzers,
Application Note
Agilent AN 1364-1, De-embedding and Embedding S-Parameter Networks Using
a Vector Network Analyzer
Agilent DE-EMBEDDED MEASUREMENTS USING THE HP 8510 MICROWAVE NETWORK ANALYZER
Agilent Network Analyzer Basics
Agilent 5989-5765EN Agilent Signal Integrity Analysis Series Part 3: The
ABCs of De-Embedding Application Note
Agilent AN 154, S-Parameter Design, Application Note
Agilent AN 95-1 S-Parameter Techniques for Faster more accurate Network
Design
Microwave Engineering, David M. Pozar, Wiley, ISBN 9971-51-263-7
Networks and Systems, D Roy Choudhury, Wiley, ISBN 0-470-20867-8
Fields and Waves in Communications Electronics, Ramo, Whinnery & Van
Duzer, Wiley, ISBN Lib Congress Catalog 65-19477
High-Frequency Circuit Design and measurements, Peter Yip, Chapman and hall,
0-442-31185-0
Sunshine Design Engineering Services
is located in the sunny San Vicente Valley near San Diego, CA, gateway to the mountains
and skies. Are you looking for new things to design, program or create and need
assistance? I offer design services with specialties in electronic hardware, CAD
and software engineering, and 25 years of experience with Test Engineering services
in RF/microwave, transceiver and semiconductor parametric test, test application
program development, automation programs, database programming, graphics and analysis,
and mathematical algorithms.
See also:
- RF Connectors and Cables
- Searching for the Q
- Hybrid Heaven
- Noise and Noise Measurements
- Solace in Solar
-
Measuring
Semiconductor Device Input Parameters with Vector Analysis
- Computing with Scattering Parameters
- Measurements with Scattering
Parameters
- Ponderings on Power Measurements
- Scattered Thoughts on
Scattering Parameters
Sunshine Design Engineering Services 23517 Carmena Rd
Ramona, CA 92065 760-685-1126 Featuring: Test Automation Services, RF Calculator
and S-Parameter Library (DLL & LLB)
LinkedIn:
Joe Cahak SunshineDesign@cox.net
Posted August 1, 2013
|